Good old Limits
n → ∞ lim 2 1 ( n 2 n ) n 1 = ?
Notation: ( N M ) = N ! ( M − N ) ! M ! denotes the binomial coefficient .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
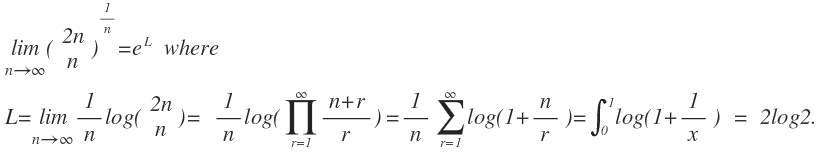
And why is that 2?
Log in to reply
the limit will be 4 Since and half of it will be 2.
I added the 1/2 just so that people would do that mistake at the end lol.
Log in to reply
Still why is 2 l o g ( 2 ) = 2 ?
Log in to reply
@Peter van der Linden – 2log2 is not 2 . If you see that I said the limit equals e^L . where L=(after evaluating) 2log2. So the value equals 4 and then after dividing by 2 it becomes 2.
Log in to reply
@Arghyadeep Chatterjee – Still don't get it... Log isn't the same as ln, so e^(2log2) is still not 4.
Log in to reply
@Peter van der Linden – Ok sorry my bad . Actually everyone are used take log as ln if no information about the base is mentioned . It is not a good thing to do in algebra but I think it is safe to do in calculus. Anyways I should have clarified that in my solution. It is actually a common practise in India to take log as ln .
Log in to reply
@Arghyadeep Chatterjee – Aah then it's a translation problem! And I thought math was such a universal language. In Europe it's common to read base 10 if there's nothing mentioned as base.
Log in to reply
@Peter van der Linden – But anyways you should have figured it out that here log was to the base e when I raised the limit to the power of e.
Log in to reply
@Arghyadeep Chatterjee – Nope I just got confused... And couldn't manage to figure it out anymore.
@Arghyadeep Chatterjee – Yeah it's matter of common and natural log.