Graphical Mechanics
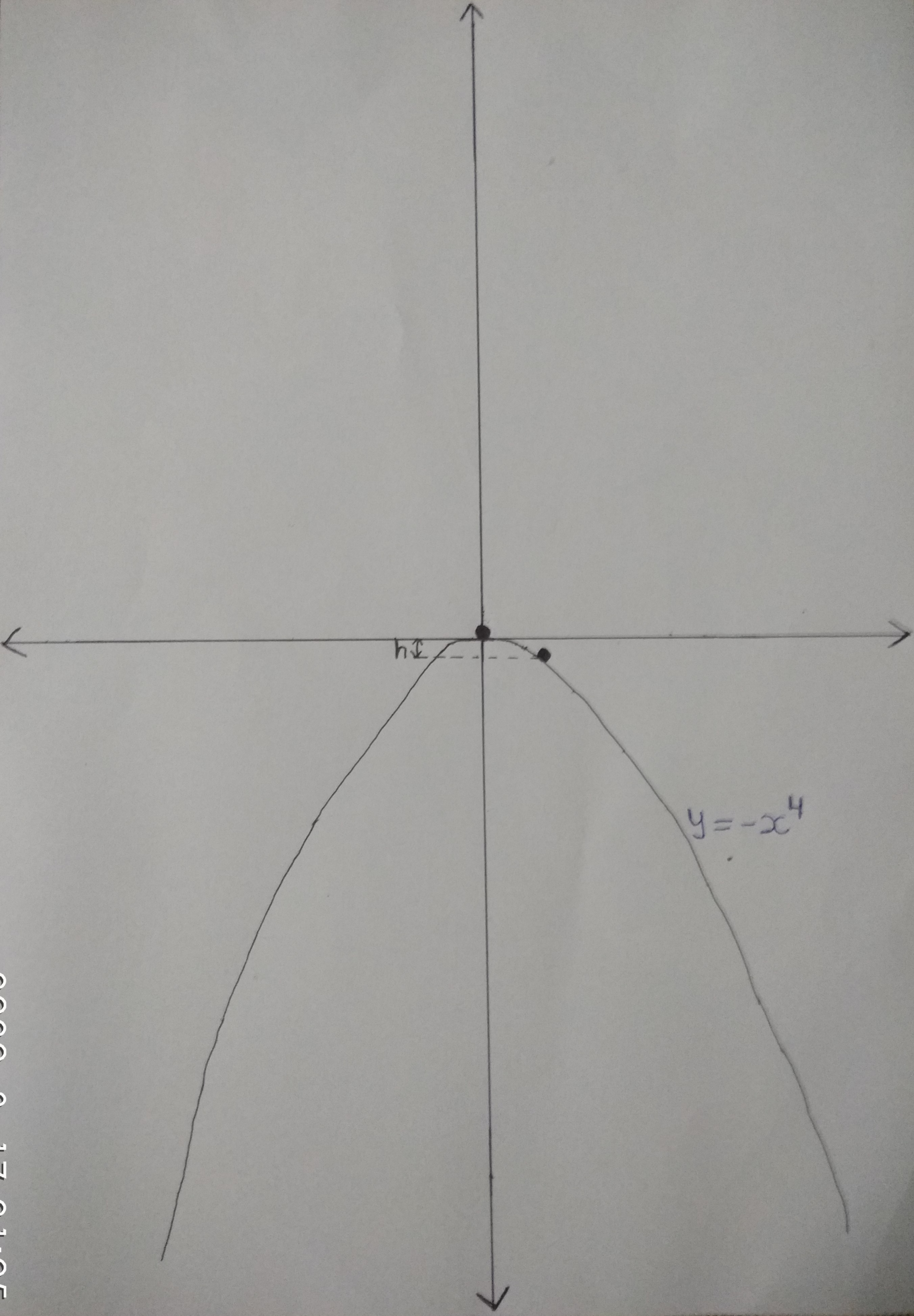
A particle of mass m is released from origin on a wedge shaped as y = − x 4 and given a very slight push to the right . After falling through height h , it loses contact with the wedge. Find h .
If h = b a where a , b ∈ N and g cd ( a , b ) = 1 , Enter answer as a + b .
Details and Assumptions:
- Take acceleration due to gravity g = 1 0 m / s 2
- Very slight push means initial velocity u ≈ 0
- All surfaces are smooth
Inspiration Aniket Sanghi
All of my problems are original
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
@Aryan Sanghi .go for my latest discussion
@Steven Chase @Krishna Karthik @Karan Chatrath @Mark Hennings try next part Graphical Mechanics (part 4)
Log in to reply
Hey thanks :) I'll try it right away.
I have to ask a question; is the spring's natural length 2 meters or 2 times the mass?
Here is the math I used in conjunction with a numerical simulation. Derive an acceleration constraint equation:
y = − x 4 y ˙ = − 4 x 3 x ˙ y ¨ = − 4 x 3 x ¨ − 1 2 x 2 x ˙ 2
Let N be the magnitude of the normal force, and let u be a unit vector in the direction normal to the curve. v is a non-unitized version of u .
v = ( v x , v y ) = ( 4 x 3 , 1 ) u = ∣ v ∣ v
Write the Newton's Second Law equations:
m x ¨ = N u x m y ¨ = N u y − m g
Substitute these two equations into the acceleration constraint equation, yielding:
N = u y + 4 x 3 u x m g − 1 2 m x 2 x ˙ 2
Then substitute N back into the Newton's Second Law equations to solve for the accelerations. Numerical integration takes care of the rest. Run the simulation until the normal force becomes negative for the first time. This is the time at which the particle loses contact with the curve. The particle falls through a height h = 4 1 before this happens.
Excellent solution sir. Thanku for sharing it with us.
Log in to reply
Thanks. Fun problem too
@Steven Chase Your solution is smallest among all solution still you have 7 upvotes. You are a very powerful guy.
Log in to reply
He is one of brilliant's top members. Famous guy indeed.
@Steven Chase sir try part 3 Graphical Mechanics (part 3)
I have solved it exactly the same way as @Steven Chase has although my nomenclature and terminology is a bit different. One may refer to his solution for details. I am attaching the simulation code here for anyone who is interested.
A plot of the trajectory of the particle is as follows. The simulation runs till the particle loses contact with the wedge. The − 0 . 2 5 y coordinate can be clearly spotted in the plots.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
|
This "acceleration constraint equation" method is generally just about as good as Lagrangian mechanics, it seems. Probably even better, since it can handle non-conservative forces too
Log in to reply
Moreover, in contrast to Lagrangian mechanics, this method allows one to compute reaction forces. However, I don't think this that this constraint equation approach is as robust as LM. This is because, as you numerically integrate for a long enough period of time, errors accumulate to a point where the constraint equation gets violated. In the case of LM, this does not happen as the constraint is very naturally accounted for, in the formulation. So in many commercial software packages that simulate rigid body dynamics and rely on the 'constraint equation' based modelling approach, the numerical integrator is combined with some sort of error minimisation optimisation scheme for the constraint equations. I read this in a source that I cannot recall.
Log in to reply
I have not tested the above claim myself but the illustrative example that the source used involved the simulation of a chaotic system (double pendulum). It was seen that over time, the links break apart. One can imagine that the small variations between successive iterations can result in large errors over time.
Log in to reply
@Karan Chatrath – Yes, I think that is certainly right. In fact, when I use this Newtonian method, I always keep track of the maximum value of a "residual" quantity. For example, for a sphere, the residual would be ∣ x 2 + y 2 + z 2 − R 2 ∣ . I only have confidence in the answer if the residual is very small at the end of the simulation. So Newton allows for computations with non-conservative forces, but Lagrange ends up being better for long-duration simulations.
Log in to reply
@Steven Chase – Precisely. But in order to have small residuals, it wouldn't be surprising if you used smaller time steps.
Log in to reply
@Karan Chatrath – Have you solved the follow-up to this? It doesn't like my answer
Log in to reply
@Steven Chase – Here is the link @Karan Chatrath sir Graphical Mechanics!! (Part 2)
@Steven Chase – Just solved it. And I get the expected answer.
Nice one. I used Matlab to solve as well; this is a hard problem.
Log in to reply
@Krishna Karthik Do you have purchased MATLAB?
Log in to reply
I'm on free trial at the moment; but when the free trial expires, I intend to purchase a license.
Python's free, but I like Matlab a lot.
Excellent solution sir. Thanku for sharing it with us. :)
The particle's position vector, velocity and acceleration are r = ( − x 4 x ) r ˙ = x ˙ ( − 4 x 3 1 ) r ¨ = x ¨ ( − 4 x 3 1 ) − x ˙ 2 ( 1 2 x 2 0 ) and so the equation of motion of the particle is m x ¨ ( − 4 x 3 1 ) − m x ˙ 2 ( 1 2 x 2 0 ) = m R ( 1 4 x 3 ) + m g ( − 1 0 ) Here m R ( 1 4 x 3 ) is the normal reaction. Taking the scalar product of this equation with ( 1 4 x 3 ) gives − 1 2 m x 2 x ˙ 2 = m R ( 1 + 1 6 x 6 ) − m g and hence R = 1 + 1 6 x 2 g − 1 2 x 2 x ˙ 2 Conservation of energy gives 2 1 m ( 1 + 1 6 x 6 ) x ˙ 2 − m g x 4 = 0 and hence R = ( 1 + 1 6 x 6 ) 2 g ( 1 − 8 x 6 ) Thus the particle leaves the surface when R = 0 , so when x 6 = 8 1 , or x 2 = 2 1 , and and hence when h = 4 1 . This makes the answer 1 + 4 = 5 .
Excellent solution sir. Thanku for sharing it with us. :)
@Mark Hennings try this problem sir Moving Wedge