Graphical Mechanics(Part 4)
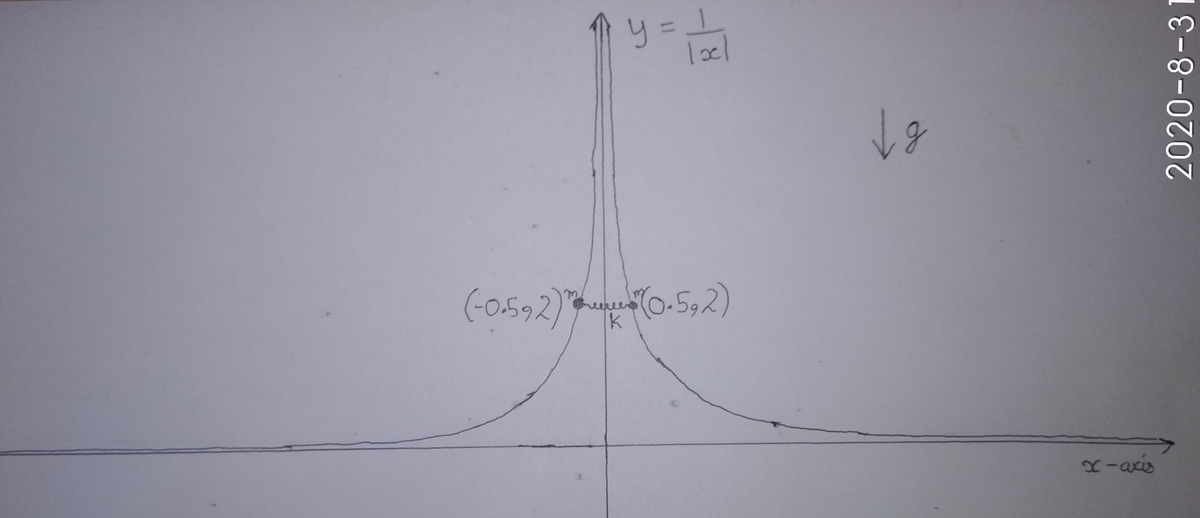
Two rings each of mass m are connected with a spring of stiffness k and natural length l as shown. Rings are constrained to move along wedge shaped y = ∣ x ∣ 1 . The system is released from rest . Find its Time Period T in seconds .
Enter answer as 2 0 T .
Details and Assumptions
-
All surfaces are smooth
-
Take acceleration due to gravity g = 1 0 m / s 2
-
Spring is ideal and has natural length l = 2 m
-
Stiffness of spring k = 2 m g N/m
-
Initially, rings are at ( − 0 . 5 , 2 ) and ( 0 . 5 , 2 ) respectively.
Inspiration Aniket Sanghi
Try similar problems by me
All of my problems are original
The answer is 27.387.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Steven Chase Awesome solution and upvoted.
@Steven Chase
can you provide a anayltical way to tackle this problem

Excellent solution sir. Thanku for sharing it with us. :) (+1)
Log in to reply
Hey bro nice problem; I'm the 3rd solver :)
Log in to reply
Thanku. It's good you're able to solve them at your age. :)
I vaguely remember solving your "bead sliding on parabola" type problems two years ago. I looked at your Lagrangian Method solutions and I think that's what got me into Lagrangian Mechanics. I also remember posting a very incorrect problem called "Frictionless Kinematic Skatepark" do you remember that?
Perhaps this solution jogged my memory... anyway, nice use of the method :)
Log in to reply
Indeed, I had a love affair with beads and parabolas several years ago, which resulted in a whole slew of problems. I do remember the name "Frictionless Kinematic Skatepark", but I don't remember the actual problem.
Speaking of Lagrange, I posted a new mechanics problem
@Krishna Karthik @Steven Chase @Karan Chatrath Try this problem by me Moving Wedge
@Aryan Sanghi why your problems are coming in top in mechanics section?
Log in to reply
I changed their topics twice, so they are coming at top. Actually they were not having levels, so I did that. :)
Log in to reply
@Aryan Sanghi
it is really a nice trick to bring any previous problem at the top.
by the way why you are crying for levels??
Log in to reply
@Talulah Riley – Actually it is just a kind of craze for me to see levels with my problems. I literally take hours and days making them, so I literally think they should get levels, isn't it?
Log in to reply
@Aryan Sanghi
–
@Aryan Sanghi See @Steven Chase sir, his almost 50% of problem has not got levels.
Still he post .
He literally post more problem and more hard problem than you.
Still he doesn't cry for levels ,isn't it?
Log in to reply
@Talulah Riley – I don't think there's anything wrong in adding levels to his problems.
@Aryan Sanghi – I thought that Brilliant had some weird algorithm that would randomly promote problems to the top of the list. Mystery solved
Log in to reply
@Steven Chase – @Steven Chase yeahhh! It is just a nonsense work of Aryan , nothing else.
@Steven Chase – Yeah, I changed the topic of a problem once; that made it into a new problem. The problem's called "There's a trick, but it's easy".
It's not the algorithm; I was going to ask Aryan the same question myself.
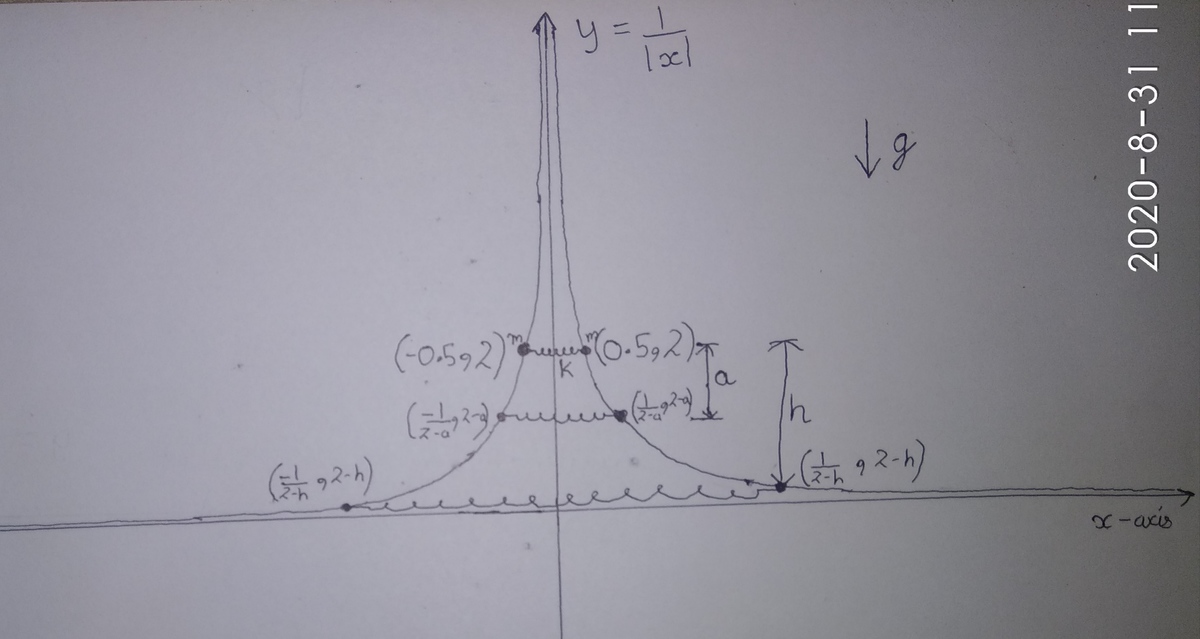
Finding h when it falls
Applying Conservation of Energy
2 1 k ( 1 ) 2 + 2 m g h = 2 1 k ( 2 − h 2 − 2 ) 2 2 1 2 m g + 2 m g h = 4 m g ( h − 2 h − 1 ) 2 2 h + 1 = 4 ( h − 2 h − 1 ) 2 h = 1 . 5 m
Finding d s
d s = 1 + ( d y d x ) 2 d y
d s = 1 + ( − y 2 1 ) 2 d y
d s = y 2 y 4 + 1 d y
Finding Time period T
Applying Conservation of Energy when they have fallen through height a
2 1 k ( 1 ) 2 + 2 m g a = 2 2 1 m v 2 + 2 1 k ( 2 − a 2 − 2 ) 2
m g + 2 m g a = m v 2 + 4 m g ( 2 − a 1 − a ) 2
v = g × a − 2 a ( 2 a − 3 ) ( a − 4 )
Putting a = 2 − y
v = g × − y ( 2 − y ) ( 1 − 2 y ) ( − 2 − y )
d t d s = g × − y ( y − 2 ) ( 2 y − 1 ) ( y + 2 ) i
g × − y ( y − 2 ) ( 2 y − 1 ) ( y + 2 ) i d s = d t
g × − y ( y − 2 ) ( 2 y − 1 ) ( y + 2 ) i y 2 y 4 + 1 d y = d t
t = g 1 ∫ 2 2 − h − ( y − 2 ) ( 2 y − 1 ) ( y + 2 ) y 4 + 1 × y i 1 d y
t = 1 0 1 ∫ 2 0 . 5 − ( y − 2 ) ( 2 y − 1 ) ( y + 2 ) y 4 + 1 × y i 1 d y
t = 0 . 6 8 4 6 s e c
Time Period T = 2 t
T ≈ 1 . 3 6 9 3 7 s e c
Therefore, answer = 2 0 T = 2 7 . 3 8 7 s e c
@Aryan Sanghi
Upvotes have been awarded.
Very nice problem and solution.
A slightly different approach. Let the coordinates of the particle on the right be:
( x 1 , y 1 ) = ( s , s 1 )
Let the coordinates of the particle on the left be:
( x 2 , y 2 ) = ( − s , s 1 )
Total kinematic energy of the system is:
T = 2 m ( x ˙ 1 2 + y ˙ 1 2 ) + 2 m ( x ˙ 2 2 + y ˙ 2 2 )
The total potential energy of the system is the sum of spring PE and gravitational PE. This comes out to be:
V = m g y 1 + m g y 2 + 2 K ( ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 − L ) 2
Plugging in the parameterization and simplifying expressions, one gets:
T = m ( s 4 s 4 + 1 ) s ˙ 2
V = 4 m g ( s − 1 ) 2 + s 2 m g
The energy conservation principle is then applied as such:
T i n i t i a l + V i n i t i a l = T + V
Simplifying the above expression gives:
s ˙ = 1 0 s 3 ( 5 s − 2 ) − 4 0 s 4 ( s − 1 ) 2 1 + s 4
Now, this equation can be separated and integrated. But before doing so, the bounds of oscillation are required to be found. It can be seen that the initial total PE is at s = 0 . 5 and the same value is obtained again when s = 2 . This can be observed by inspection or by the plotting the potential energy as a function of s . So the system oscillated between 0 . 5 ≤ s ≤ 2 . The time period can be found by separating the variables and integrating between the bounds. The resulting expression must be multiplied by 2 as movement from one bound to another occurs in half a time period.
Thus:
T = 2 ∫ 0 . 5 2 1 + s 4 1 0 s 3 ( 5 s − 2 ) − 4 0 s 4 ( s − 1 ) 2 d s
The rest is all numerics. The answer comes out to be: 2 0 T ≈ 2 7 . 3 8 7 4 3 3 6 2 3 2 2 6 7 1
I just noticed that you solved the problem using energy conservation as well. I guess that makes my solution redundant. Thanks anyway for posting this problem. It is a good one
Log in to reply
Thanku very much sir. An excellent Solution too from you. :)
@Karan Chatrath
sir if you want you can post solutions of magnetism problems in community.
Thier solution will not be reductant and will be deeply appreciated.
Thanks in advance.
Log in to reply
Yes, I will solve them, as and when I can. I have solved a few till now
This problem is fairly convenient to do with Lagrangian mechanics. Let x be the horizontal coordinate of the particle on the right.
x = x y = x − 1 x ˙ = x ˙ y ˙ = − x − 2 x ˙
Kinetic energy:
T = 2 2 1 m v 2 = 2 2 1 m ( x ˙ 2 + y ˙ 2 ) = m ( 1 + x − 4 ) x ˙ 2
Potential energy:
V = 2 m g x − 1 + 2 1 k ( 2 x − ℓ ) 2
Lagrangian:
L = T − V = m ( 1 + x − 4 ) x ˙ 2 − 2 m g x − 1 − 2 1 k ( 2 x − ℓ ) 2
Equation of motion:
d t d ∂ x ˙ ∂ L = ∂ x ∂ L
Evaluating results in:
x ¨ = 2 m ( 1 + x − 4 ) 4 m x ˙ 2 x − 5 + 2 m g x − 2 − 2 k ( 2 x − ℓ )
Numerically integrate until x ˙ < 0 for the first time. This time corresponds to a half period. Simulation code is attached.