Great Circles
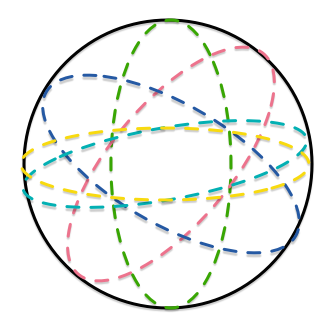
Given a sphere, a circle is called a great circle if it is the intersection of the sphere with a plane passing through its center. Five distinct great circles can dissect the sphere into regions.
Let and be the minimum and maximum values of , respectively. Submit your answer as the concatenation of and .
For example, if you think that , , then your answer is .
The answer is 2210.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We consider m and M as functions of k , the number of great circles drawn on the sphere. Let M k ( m k ) denote the maximum (minimum) number of regions in which the sphere can be dissected by k great circles. Then M 1 = m 1 =2.
Assume that there k great circles drawn on the sphere, and the sphere is dissected into a k regions. When the ( k + 1 ) s t great circle is drawn, it will cut through a certain number of regions. One more region will be produced by each region it cuts through. The ( k + 1 ) s t great circle intersects the other k great circles, and every pair of adjacent points forms an arc that cuts through an existing region.
Note that two distinct great circles must intersect at two points. Hence any number of great circles have a minimum of two intersection points, and m k + 1 > = m k + 2 . Thus, m 5 > = m 4 + 2 > = m 3 + 2 + 2 . . . > = m 1 + 8 = 1 0 . It is easy to see that we can obtain 10 regions by drawing five great circles through two diametrically opposite points, so m = 10. On the other hand, the ( k + 1 ) s t great circle will have at most 2k intersection points with the first k great circles, leading to 2k new regions. By rotating the circle slightly along any axis, we can indeed obtain 2k new intersections. Hence M k + 1 = M k + 2 k , and we obtain M = M 5 = M 1 + 2 ( 1 + 2 + 3 + 4 ) = 2 2 .
Hence M + m = 3 2 , and the required answer is 5.