Great Jordan
Jordan is practicing three-point shots using old equipment. This time, he was pointing directly to the old, loose basket and just at the moment he is throwing the ball, the basket starts to fall. Assuming that, if the ball gets to the basket, it will always get there before the ball gets to the ground, qualitatively, with how much velocity does he needs to throw the ball to score the three points?
Based on a Sears-Zemansky example.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Great, simple solution! In deed, I made this problem inspired in the shooter and the monkey problem!
Jordan is so good he would never miss. Period.
:P
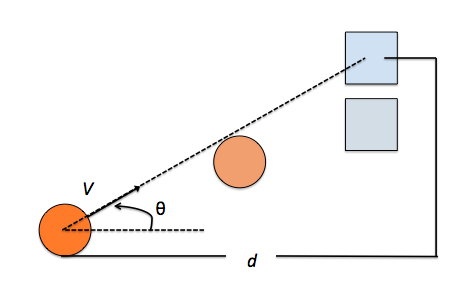
From the image, which I hope is self explanatory, we can identify the positions of the basket ball and the falling basket as x , y , y B respectively ("B" for basket, not ball or basket ball) which are given by:
x = V t C o s θ ; y = V t S i n θ − 2 g t 2 ; y B = d T a n θ − 2 g t 2 ;
When the ball gets to the basket: y = y B ⇒ V t S i n θ = d T a n θ
and x = d ⇒ t = V C o s θ d
So: V t S i n θ = V C o s θ V d S i n θ = d T a n θ Meaning that the " V t S i n θ = d T a n θ " condition needed for the ball to get to the basket is always met, independently of the velocity with which it is thrown.
The correct answer is "With any velocity" (Yes, he is that good :P) Cool video demonstrating experimentally this fact
That's an assumption, not a solution.
Log in to reply
Well, is the best solution I could work through and I think that it is, in fact a solution because it makes sense. If you notice, the that V t S i n θ = d T a n θ is independent not only of the initial velocity of the but of the acceleration due to gravity so image that this acceleration is zero: the basket won´t fall down and the ball will follow a straight path directly to the basket. Also, this problem is based on a well-known fact; check this video out and tell me what do you think: Cool video demonstrating experimentally this fact
Log in to reply
V could be 0, so the basket ball would have never moved. What if the velocity is 1mph?
Log in to reply
@Mateo Matijasevick – Yes, you are rigth, for the solution I gave to be valid, I considered that the ball has enough velocity to get to the basket. But, the problem states: "Assuming that, if the ball gets to the basket, it will always get there before the ball gets to the ground." If the problem´s statements aren´t clear enough, please tell me what causes you trouble to understand so I can improve the composition.
Log in to reply
@Erasmo Hinojosa – "Assuming that, if the ball gets to the basket, it will always get there before the ball gets to the ground." does not mean that the ball will always get to the basket with any initial velocity, unless that for every possible velocity value, the basket can be placed wherever we want.
Log in to reply
@Mateo Matijasevick – You are right again; it does not mean that the ball will always get to the basket with any initial velocity but demonstrating that it does is simply what the problem is. Did you saw the video I shared some comments above? I really invite you to check it; it is pretty cool.
Log in to reply
@Erasmo Hinojosa – I saw it. It's amazing! The problem is great, I just think that is a little bit ambiguous. What does it mean "with any velocity"? And, what is "a low velocity"? I really enjoyed the reasoning of the problem but you need to be clearer with the options.
Log in to reply
@Mateo Matijasevick – Yeah, I would, probably, change all the problem's composition. I wrote this one myself but I know that Sear-Zemansky has a similar problem so would look for it and write this problem as the one in the book.
Hitting the basket with the ball and having the ball go into the basket (and thus scoring) are two different things. The description above seems to describe the former.
Log in to reply
Yeah, sorry for making it ambiguous... I´ll try to change the description to make it clearer.
It is just Galileo's first law..
Oh, really? I heared before about Galileo's laws. Where can I read more about them? I'm really interested in learning more about them.
The relative acceleration of the ball is with respect to the basket is zero.Since the ball is directed towards the basket initially the ball will always hit or go into the basket. This is similar to the shooter and the monkey problem.....