Greatest Area
Which triangle has the greatest area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Very nice solution. Thank you so much for sharing it.
Log in to reply
How can 3 be equal to 5. It can proved mathematically though. Butthe question is how?
Visually played around with Heron's formula a bit, and realized that if you've skewed a triangle's shape by moving one of its three points (say 'A'), then that triangle's area will remain unchanged as long as that point is moved along a path parallel to the line created by the two other points, (the line 'B-C'). Here's a gif I made:
I don't see why you brought in Heron's formula, but that aside this comment hits the nail on the head. A=bh/2, so it doesn't change if b and h remain unchanged.
And I like your gif.
Log in to reply
Thanks, you've raised an important issue. Have a look at the updated solution. I took your comment into account when I created the new animation. I think you will find it satisfactory.
Log in to reply
How can 3 be equal to 5. It can proved mathematically though. Butthe question is how?
How can 3 be equal to 5. It can proved mathematically though. But the question is how?
Triangles B has vertex that can be moved parallel to its opposite side so that the vertex lands in a nice position. Nice enough that calculating the new resulting triangle's area is immediate. The same applies to D. This is very pretty observation! Not sure why you'd bring Heron's up either though.
This is true of triangles A, C and E, each of which has one equal side. But triangles B and D do not have the same base. If the length between each dot is 1 unit, then B and D have one side that is equal to the square root of 2. Thus, your lovely gif is not relevant for all of the triangles.
Log in to reply
Thanks, you've raised an important issue. Have a look at the updated solution. I took your comment into account when I created the new animation. I think you will find it satisfactory.
Your GIF applies to other questions I've encountered on Brilliant. And it's way cool.
Good work... Thanks a lot! 😀😀
Very nice, good and cool solution
I think I just fell in love with you?! 😍😍😍
Each triangle has zero interior lattice points and three boundary lattice points (the three vertices), so by Pick's Theorem , the area of each triangle is 1/2.
Moderator note:
To give a little more detail on Pick's Theorem (for those who don't want to click a wiki link), it states that the area of a figure with all points on a lattice grid is
( number of points coinciding with boundary ) / 2 + ( number of points inside the figure ) − 1
So for all the points in the example the area is 2 1 since
3 / 2 + 0 − 1 = 1 / 2 .
The wiki includes a full proof , or if you prefer more detail, you can go through a 3-part quiz sequence which leads through the proof (start with "Pegboard Rectangles").
Thank you for sharing your solution.
Pick's Theorem!
that's a neat Theorem!
How can 3 be equal to 5. It can be proved mathematically though. But the question is how and why?
Pick's theorem is just great for such problems. Nice problem @Hana Wehbi
Log in to reply
@Mahdi Raza , Thank you. Also, your problems are nice too.
Here is a similar problem
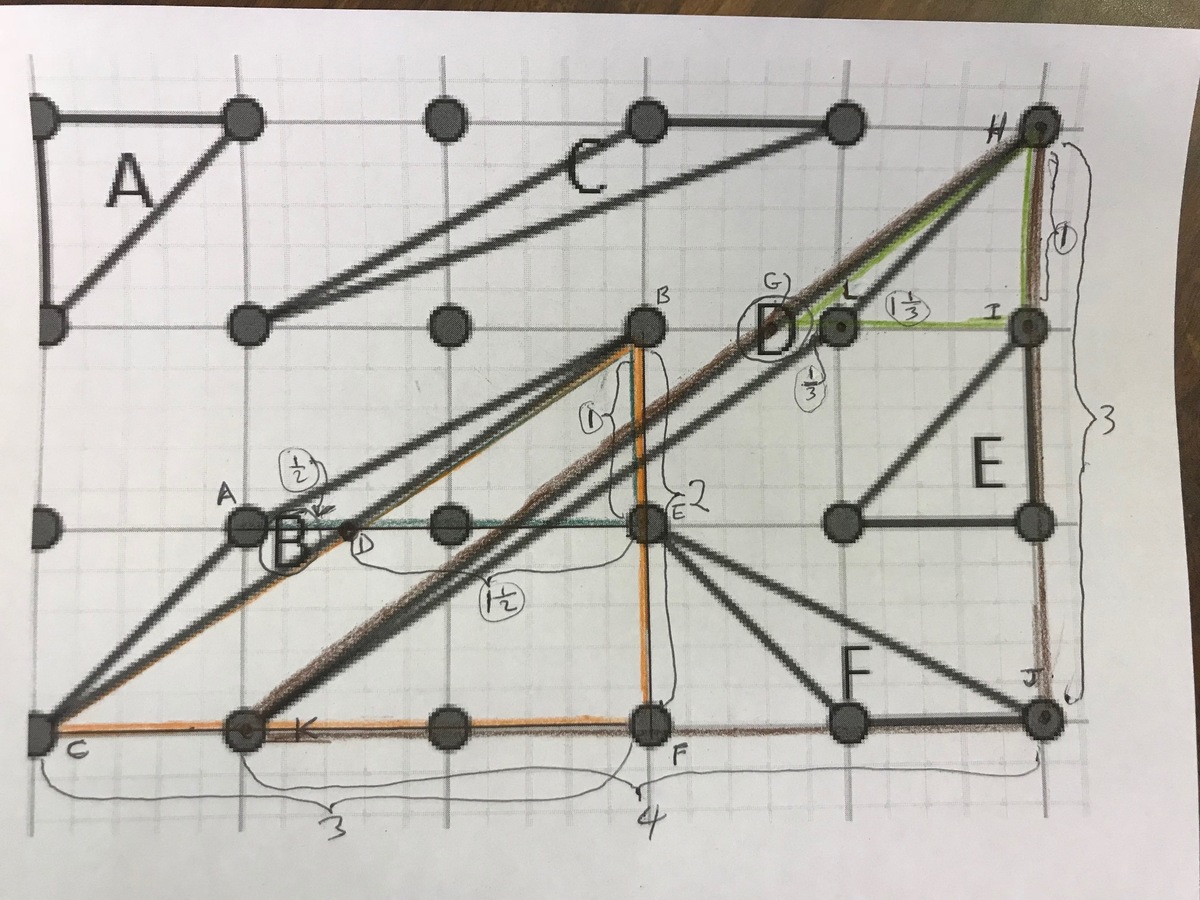
It is easy to see that triangles A, C, E, & F all have base and height of 1 unit and area of 2 1 square units. For triangles B & D, I labelled the vertices of the triangles and other relevant points in the diagram. Starting with triangle B, I divided the triangle into 2 sections by drawing BD and extending it to E. △ B C F ∼ △ B D E . ∴ D E B E = C F B F = 3 2 = 1 2 1 1 ⟹ D E = 1 2 1 ⟹ B D = 2 1 . So the upper and lower parts of triangle B both have a base of 2 1 and a height of 1 and an area of 4 1 giving a total area of 2 1 . Now for triangle D, the method is similar. Divide the triangle into 2 by drawing GI. △ H G I ∼ △ H K J . ∴ G I H I = K J H J = 4 3 = 1 3 1 1 ⟹ G I = 1 3 1 ⟹ G L = 3 1 . So the upper and lower parts of triangle D both have a base of 3 1 and heights of 1 and 2 respectively. The total area is again 2 1 . Thus all the triangles have the same area.
Thank you for sharing your solution.
I still don't understand how you achieved finding areas of B and D.
Log in to reply
Let me know which part of the solution is hard to follow and I will try to explain it
Log in to reply
I used Heron's Formula for B and D. The results show that D is bigger than ACEF (which is 12.5) which is bigger than B. How is it possible that all have the same area like you demonstrated?
Log in to reply
@A Former Brilliant Member – Sorry, I got busy with teaching students. I tried Heron's formula just now and got 2 1 for areas of both B & D. For triangle B, I used sides 2 , 5 , 1 3 . For triangle D, I used sides 2 , 1 3 , 5 . Check your calculations - you will probably find where you went wrong. Hope that helps :)
Log in to reply
@Richard Costen – A, C, E all hava a base length of 1 and a height of 1. For B and D let me rotate the paper by 45° clockwise: A base length of sqrt(2) and a height of 1/sqrt(2) is now apparent.
Log in to reply
@Juergen Weigert – Oops, base length 2 and height of 2 1 in pretty print :-)
I'll do my best to help with triangle B. Once B makes sense, hopefully you'll be able to see how Richard used the same trick for triangle D.
The important thing is to notice that Richard has drawn a line between two points on the diagram. The point labelled A, and a point labelled D. If you start at the far bottom left of the diagram (which is labelled "C"), then you can find point A by going one dot to the right, and one dot up. Point D is a little harder to spot. If you start at point A, then point D is directly to the right. D is halfway between point A and the next dot. (The "D" is quite small, and I missed it at first because it's right next to another line that Richard drew, and together they look kind of like an arrowhead or a leaf.)
Once you draw this line in (between A and D), you've split triangle B into two smaller triangles: The triangle made between point A, point D, and point B (the point at the top of the triangle), and the triangle made between point A, point D and point C (The far bottom left point in the diagram).
Think of the line A-D as the "base" of both small triangles. It's a horizontal line, so the "height" will be the vertical height of each small triangle. You should be able to see that the height of each of these triangles is 1 unit. So you can calculate the area of each little triangle using ½h×b. We just need to know how long the line "AD" is.
Richard used the concept of "similar triangles" to work out the exact location of point D. I'll use a different (but related) method. The long line between point C and point B goes three units to the right, and two units up. So the halfway point of the line will have gone half as far to the right (one and a half units) and half as far up (1 unit). Point D is exactly one unit higher than C, so it is exactly one and a half units further right than C. That puts it exactly half a unit to the right of A.
So triangle B is split into two smaller triangles. The both have a base of ½ a unit, and a height of 1 unit.
Area of triangle B = Area of top part + Area of bottom part = ½h×b + ½h×b = ½×½×1 + ½×½×1 = ½.
Does that make sense?
Log in to reply
Very clear explanation. Keep on posting to other problems :)
Very nice solution for B and D. Really BASIC.
In my case I've been using the longest side of triangles as a diagonal of a square or rectangle and then substracting the remaining area. Let's say that the distance between each dot is x. A = (x*x)/2 (because it's the half of this square) = x^2/2 = 0,5x^2 B = 6x^2/2 (half of the rectangle 2 by 3 dots) - x^2 (the square 1 by 1 dot left to the letter B) - x^2/2 (small triangle as a half of 1 by 1 square in the left, down corner) - 2x^2/2 (triangle as a half of a 1 by 2 rectangle having one side of the B triangle as diagonal) = 3x^2 - x^2 - 0,5x^2 - x^2 = 3x^2 - 2,5x^2 = 0,5x^2 And apply it to every triangle.
Each triangle has the same area equal to 0.5 units .
it can be calculated like this
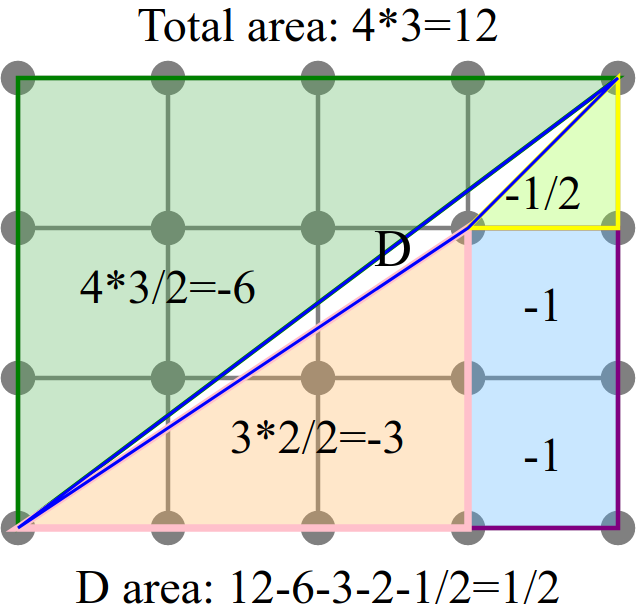
Nice solution. Thank you.
A, C, E, and F all have a base and height of 1. B and D have a base of √2 and height of √2/2 (create a line connecting the 2 closest vertices and see that the 3rd is half a diagonal distance away from the line.) All have an area of 1/2.
Thank you for sharing your solution.
where is F?
The area of a 2D parallelogram can be calculated by treating two of the sides as vectors a and b , and then computing ∣ a x b y − a y b x ∣ . The area of the triangle is half that of of the parallelogram, A = 2 1 ∣ a x b y − a y b x ∣ . Since all these triangles are on a grid, it's easy to compute these components:
- A: Starting from the bottom left corner, we identify a A = ( 1 , 1 ) and b A = ( 0 , 1 ) . Then the area is A A = 2 1 ∣ 1 ⋅ 1 − 1 ⋅ 0 ∣ = 2 1 .
- B: We have a B = ( 3 , 2 ) and b B = ( 1 , 1 ) . So, A B = 2 1 ∣ 3 ⋅ 1 − 2 ⋅ 1 ∣ = 2 1 .
- C: Here, a C = ( 3 , 1 ) and b C = ( 2 , 1 ) . So, A C = 2 1 ∣ 3 ⋅ 1 − 1 ⋅ 2 ∣ = 2 1 .
- D: Here, a D = ( 3 , 2 ) and b D = ( 4 , 3 ) . So, A D = 2 1 ∣ 3 ⋅ 3 − 2 ⋅ 4 ∣ = 2 1 .
- E: Starting from the top left, a E = ( 2 , − 1 ) and b E = ( 1 , − 1 ) . So, A E = 2 1 ∣ 2 ⋅ ( − 1 ) − 1 ⋅ ( − 1 ) ∣ = 2 1 .
This turns out not to be the most elegant way to solve this, since we can apparently use Pick's Theorem, but this method has broader applications. For a three dimensional triangle, the area of the triangle is given by a vector cross product 2 1 ∣ a × b ∣ - we can see the above formula is a special case of a cross product where the third component is zero.
An almost identical calculation is also very important in real-time 3D computer graphics, where it's used to compute an 'edge function' and 'barycentric coordinates' determining whether a particular pixel is inside a triangle, and if so, how to interpolate quantities defined on the vertices in a perspective-correct way. In a rasterisation process, after the vertex shader has run, you have the positions of each vertex projected onto 2D plane of the screen. So, much as in the above case, you have the x and y components of the edges as vectors.
Suppose you have a point p and you want to know if it's inside a triangle with vertices v 1 , v 2 , v 3 . For each edge - take for example the edge 12 - you can find two vectors p − v 1 and v 2 − v 1 , and then calculate ( p x − v 1 x ) ( v 2 y − v 1 y ) − ( p y − v 1 y ) ( v 2 x − v 2 y ) - this is twice the 'signed area' of a triangle defined by the two vertices and the point, and it is positive if the point is on one side of the edge, and negative if it is on the other. By computing this for all three edges, you know the point is inside the triangle iff all three edge functions are positive. Moreover, these signed area functions turn out to be exactly what you need for finding, for example, the texture coordinates at this point in a perspective-correct way.
For more information on that and the rasterisation algorithm in general, see Scratchapixel's wonderful tutorial .
Nice solution. Thank you.
Oh wow, the link you've shared is a fantastic article. I guess I have booked up my entire weekend reading this. Thanks!
Log in to reply
Scratchapixel is a fantastic site, I'm glad I could share it :)
As others have said, A, C, E, & F all have base 1 and height 1. For the other 2, treat the 45 degree side as the base. Now moving the 3rd point parallel to that maintains the height. You can move those point to where they also make 1 by 1 triangles, thus the same area.
Thank you for sharing your solution.
I just guessed.I had this feeling that all triangle are same because points A,B and C are three points and triangles are stretched at one of these points.
There are zero interior points[I(P)] in each of the triangles and 3 boundary points[B(P)] or vertices in each of the triangles. Therefore by Pick's Formula, Area of each triangle =I(P)+(B(P)/2)-1=0+(3/2)-1=1/2 Therefore all the triangles have the same area...
Thank you for sharing your solution.
You can shear triangles C and E about their horizontal sides, and B and D about their sides angled at 4 5 ∘ , so as to produce a triangle congruent to A in each case. Since shearing preserves area, it follows that triangles B, C, D and E all have the same area as A.
Thank you for sharing your solution.
You can simply use base x height /2 for the area of triangles A, C and E to get 1/2 for all of them.
For triangles B and D you can extend the triangles and by working out the total area - added area, you get the original area of the triangle.
If you were to label all the points on the grid as A to F horizontally and 1 to 4 vertically from the bottom left corner, (like a chessboard) the extension can be better expressed. First I will start with triangle B. By leaving points A1 and D3 and creating a new point C3, you can form a triangle with area 1x 2 /2 = 1 as the total area. The added area (B2, C3, D3) is mathematically similar to triangle E and has an area of 1 x 1 /2 = 1/2. Therefore by taking away 1/2 from 1 we get the area of triangle B to be 1/2.
The same principal can be applied to triangle D. By creating a triangle with points B1, C1 and F4 we get (1x3 /2 ) - (1x2 /2) = 1/2 as the area of triangle D. Thus all the triangles have the same area.
Reuben - age 14
Thank you for sharing solution.
According to Pick’s Theorem, the area of a lattice polygon is 2 B + I − 1 , where B and I are the numbers of boundary and interior points respectively. Each one of the given triangles has area A = 2 3 + 0 − 1 = 0 . 5 square units.
Just create parallelograms using the triangles as one half and you will notice that the triangles that form the parallelograms from A,C,F, and E all have height and base 1. Since the area of the triangle is half the area of the parallelogram you get 1/2. You could then calculate distance for B and D.
My solution was to have my friend go on his computer and tell me the answers btw I am the highest level in everything in my class 🤣
For triangles A, C, and E, take the horizontal side as the base. Then they all have bases and heights of 1, so area 1/2. For B and D, take the side that's a single diagonal as the base. It has length sqrt(2). The heights are then 1/2 of a diagonal, so length 1/sqrt(2), and the areas are again 1/2.
By assuming points to be in a Cartesian plane area of each triangle =1/2
I don't understand. How do you immediately know that their area are all equal to 1/2?
Treat the dots as points in a xy plane. Find coordinates for the vertices of the triangles. Use determinants or any other method to calculate area
Please help me find the areas of B and D!
Look at previous solutions : )
The most conventional method is via shoelace formula .
Visually played around with Heron's formula a bit, and realized that if you've skewed a triangle's shape by moving one of its three points (say 'A'), then that triangle's area will remain u n c h a n g e d as long as that point is moved along a path parallel to the line created by the two other points, (the line 'B-C'). Here's a gif I made:
Click here for the interactive version.
In this week's problem, triangle E's area will remain unchanged as long as its top-most point is shifted horizontally anywhere along the third row of dots.
Similarly, triangle C's area will remain unchanged as long as its bottom-most point is moved anywhere along the second row of grey dots.
Triangles B and D are a bit tougher to see, but let's say the bottom left grey dot is the the origin (0,0) of a coordinate system x,y. If you squint (or bring out a ruler) you'll see that in triangle B for example, its right-most dot can be moved diagonally along any of the grey dots with the 'coordinates' (1,0), (2,1), (3,2), (4,3).
So, because all triangles in this week's problem are essentially the same as triangle A but with their shape changed by shifting one of the points along a line parallel to the two other points, all the triangles have the same area.
A trivial consequence of Pick's theorem perhaps (as others have mentioned), but I found it's still a nice visual reminder of what the theorem actually entails.
EDIT: Yes, you guys are correct -- there was no need for me to mess around with Heron's formula. I could have just used good old Area=(base)(height)(0.5) , and since neither base nor height is changing, its area will of course stay the same. To be honest, I was just playing around in Geogebra and happened to find something I thought was cool, so I figured I'd share it with the community. Didn't expect this to get up-voted to one of the top solutions. As a way of thanking you for all your up-votes I have made another animation for you (screenshot below, gif file size was too large). I may have gone a bit overboard with the animations in this new one, but all it's really showing is that none of the triangles change their base or height, and therefore their area doesn't change.
Click here for the interactive version.