A Non-Symmetric Expression?
If a and b are positive numbers, find the maximum value of a b ( 7 2 − 3 a − 4 b ) .
The answer is 1152.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I will be using a slight different method of multivariable calculus,
Let y = 7 2 a b − 3 a b 2 − 4 a b 2 ,
Partial differentiation of y with respect to a and b yields,
∂ a ∂ y = 7 2 b − 6 a b − 4 b 2 and ∂ b ∂ y = 7 2 a − 3 a 2 − 8 a b and for minimum or maximum value ∂ a ∂ y and ∂ b ∂ y = 0 .
Now we have got two variables and two equations we can solve for a and b , after solving the equations note that for maximum value of y we must take a = 8 and b = 6 instead of a = 0 and b = 0 (as it would minimum value of y).
Hence,
y ∣ m a x = 7 2 ( 8 ) ( 6 ) − 3 ( 8 ) 2 ( 6 ) − 4 ( 8 ) ( 6 ) 2 = 1 1 5 2 .
You need to prove that it is a maximum point, but not a minimum point / saddle point.
I don't understand. Why must a = 3 3 6 − 2 b and b = 8 7 2 − 3 a ?
Log in to reply
Max values of f and g are equal and equalities f=3b((36-2b)/3)^2 and g=4a((72-3a)/8)^2 hold if and only if -3b(a-(36-2b)/3)^2=0 and -4a(b-(72-3a)/8)^2=0, and since a and b are positive reals, (different from 0), it has to be a-(36-2b)/3=0 and b-(72-3a)=0.
Log in to reply
Got it. Thanks.
Hope you don't mind this unsolicited advice, but your working would be greatly improved with LaTeX .
Log in to reply
@Pi Han Goh – Thanks for advice, I'm new here and I've never worked with LaTex, I'll try it in my next posts. :)
Using AM GM for 3a+4b we get -(3a +4b)<=2(√12ab). Now put ab=m and we get ab= 12/√3. And finally answer
It is non-symmetric. Let us make it symmetric by the transformation a ′ ⇒ 4 a and b ′ ⇒ 3 b . The expression becomes 1 4 4 a ′ ∗ b ′ ( 6 − a ′ − b ′ ) which is symmetric.Now if we interchange the new variables the value of the expression remains unchanged.It is also a polynomial in two variables and hence smooth and differentiable infinitely.Therefore, it follows that the extrema will occur along the line a ′ = b ′ .One quickly finds the value by converting it into a one dimensional polynomial and finds the extrema.
You still need to prove that it's a maximum value, and not a minimum value or saddle point.
Log in to reply
Well assumed that in finding the extrema for a one dimensional ;polynomial the user also finds the nature of the extrema.(In this case it is a maxima)
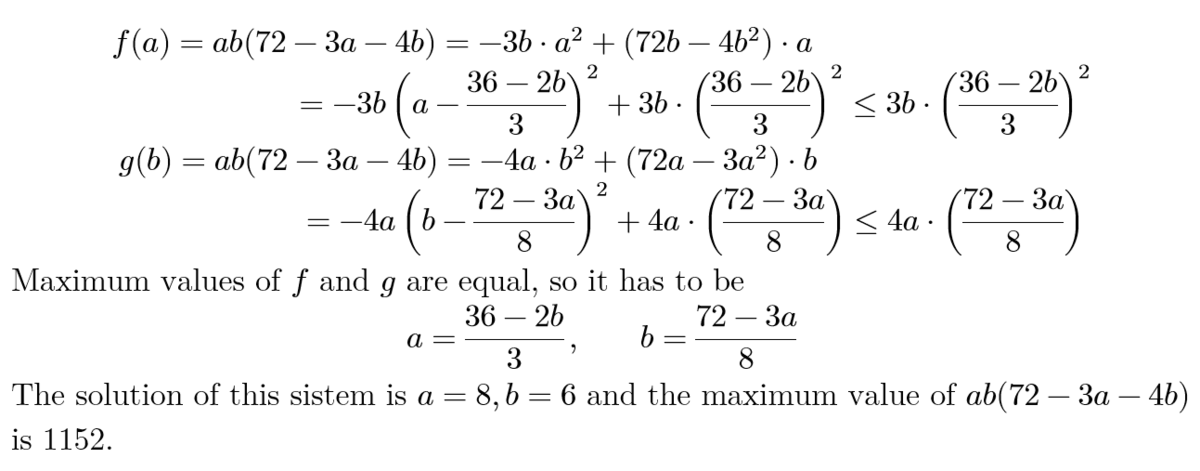
Relevant wiki: Applying the Arithmetic Mean Geometric Mean Inequality
Let A = a b ( 7 2 − 3 a − 4 b ) .
If 7 2 − 3 a − 4 b ≤ 0 , A ≤ 0
If 7 2 − 3 a − 4 b > 0 , applying the AM-GM inequality, we have:
A = 1 2 1 ⋅ 3 a ⋅ 4 b ⋅ ( 7 2 − 3 a − 4 b ) ≤ 1 2 1 ⋅ ( 3 3 a + 4 b + ( 7 2 − 3 a − 4 b ) ) 3 = 1 1 5 2
The equality holds iff 3 a = 4 b = 7 2 − 3 a − 4 b ⇔ { a = 8 b = 6 .
So max A = 1 1 5 2 , when a = 8 ; b = 6