Guarding the Ring
An art museum wants to build a new gallery. The floor plan is an annulus (a ring shape bounded by two concentric circles), with walls constructed on both circles. The outer circle has a radius of 1 0 m , and we are not able to see through the inner circle.
The museum will hire guards to ensure that the public does not touch the artwork. Each guard will stand at a fixed spot, but can look in all directions from that spot.
If they can afford to hire only 4 guards, and every part of the gallery must be visible to at least one guard, then what is the maximum ( supremum ) possible radius of the inner circle in meters?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
As always, with finding a max/min, we need to 1) show that no higher/lower number works and 2) show that this number works
This solution does 2), giving a configuration that "just works". However, it doesn't provide a clear description of 1.
Do you see how to fill in this gap?
Hint:
Think about what the constraints are. In particular, the optimal case requires that the line of sight is tangential to the inner wall. How can we quantify this idea mathematically?
@Nicholas James Do you see how to finish out the proof?
Log in to reply
I've added a bit about the guards being able to see less than a quarter of the inner wall if the circle were any bigger, but I could formalise it
Log in to reply
Right. So the best way to formalize it, would be to say:
Given an inner radius R , the maximum proportion of the inner wall that a guard could protect is 2 π cos − 1 1 0 R , which is achieved when the guard is at the outer wall. If we had n guards, then at least one of them must guard n 2 π R of the perimeter (by the pigeonhole principle).
Log in to reply
@Calvin Lin – OK, I've added some more. Hopefully we're about there now :)
Log in to reply
@Nicholas James – Getting there.
Be careful with phrasing in cases where we're bounding on two sides. For example, when saying "we want this angle to be as small as possible", to me, we want this angle to be as large as possible, so we can use fewer guards. However, I agree that the smaller the angle, the larger the radius.
Instead of "Using the pigeon hole principle, we would ideally like each guard ...", it is that "at least one of the guards must see ..." From there, we get a constraint on the angle.
Combining these 2, the argument would be
- By PP, there is a guard that sees at least 9 0 ∘ of the perimeter.
- This means that 1 0 R = cos x ≤ cos 4 5 ∘ .
- Hence, R ≤ (answer).
Nice problem. If they can only afford 3 guards then the maximum radius would be 5 metres, (the radius of the incircle of the equilateral triangle inscribed in the outer circle).
And n guards is a nice extension. Interestingly 3 guards is the minimum.
But wouldn't an inscribed octagon be The answer because with the square their sight lines are overlapping?
Log in to reply
The tangent lines to the interior circle are really the sight lines that the museum guards have as cut off by said interior circle.
For now, let's assume that all guards lie on vertices of the polygon we are choosing
Hence, if a section of the museum lies inside the polygon but outside the inner circle, then a guard must be on the vertex of the section of polygon that bounds the region (can you see why?)
This results in the number of guards being needed is n , where n is the number of sides of the chosen polygon.
Hence, for a square, there are four sections that can't be seen by guards on adjacent vertices, but that's ok because we have four guards.
In the case of an octagon, we have 8 regions that can't be seen by guards on adjacent vertices, but only four guards, which is why this is not possible
Log in to reply
Oh this is a nice explanation, I was trying to explain it in words but I can't seem to verbalize it. Thanks!!
That's a good idea, but the entire inner wall must be seen, and an octagon would require 8 guards for this. With the guards in this position, each can see 1/4 of the inner wall. The 4 small areas that are between the square and the inner wall are the parts that can be seen by one guard and one guard alone.
I found 9,849m But i used this configuration. Cause each point just need to be seen by ONE guard. So we can extend the Radius.
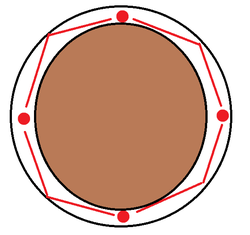
But correct me if the calculation is wrong.
Log in to reply
Unfortunately there are some points in your configuration which are not visible by any guard (shown by the white region). Those points would be visible by a guard if we move the guards to the perimeter of the outer circle and reduce the radius of the inner circle.
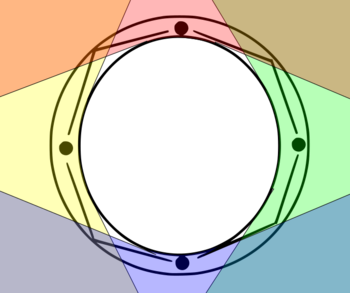
Log in to reply
That's a fantastic picture!
Thanks! Nice explanation
@Pranshu Gaba I wish I could create as nice graphics, but I fear the haphazard placement of your guards/dots gives a misleading result.
In order to be a consistently solvable problem, we actually need more information.
Do guards stand at the inner circumference?
Halfway between both circumferences?
At the outer periphery?
These will all significantly impact the "sidedness" of the polygon due to the changing angle measure of its vertices. Given the absence of these details, as Mathematicians, we assume optimization and work from there.
That will make our "guards" massless, dimensionless points that reside precisely placed on the outer circumference in order to maximize their field of view.
In that case, the largest sized inner radius that still allows at least one of the four guards to see every location will exist when they each can view precisely 90 degrees of the inner circle's circumference. Since the guards lie outside that circumference, their angle of view needed to cover that interior 90 degrees will, by definition, be less than 90. Therefore, in order for the guards' optimized field of view to equal the 90 degrees of arc, their angle of view between those extremes must be greater than 90 proving, at the very least, that using an inscribed square as the inner circle's bound leaves unexplored solutions that are larger. (But agreed, using an octagon leaves 8, wedge-like slices unviewable by any guard.)
Log in to reply
I agree, the question hasn't specified where the guards are standing. We have the freedom to place the guards anywhere in the annulus that we want. For a given ratio of outer radius to inner radius, we want to place them such that we require minimum number of guards. The optimal position can be obtained by drawing a regular polygon with as less sides as possible such that it fits entirely in the annulus and then placing guards at every vertex of the polygon.
It is best to place guards on the outer circle. We can see that the further a guard is from the inner circle, the more area it can see. If the guards stand at the inner circumference, then we would require infinite number of them. The number of guards required would decrease as we place them closer to the outer circumference.
Why come from
Log in to reply
Why come from √2
Log in to reply
We get 2 when we simplify 2 0 0 .
2 0 0 = 1 0 0 × 2 = 1 0 0 × 2 = 1 0 × 2
well, thats my answer! :) gotta see the challenge master note for further thinking
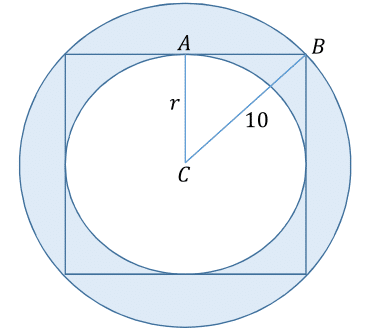 Triangle
A
B
C
is an isosceles triangle with a right angle at
A
, so
2
r
2
=
1
0
0
,
r
=
2
1
0
=
5
2
Triangle
A
B
C
is an isosceles triangle with a right angle at
A
, so
2
r
2
=
1
0
0
,
r
=
2
1
0
=
5
2
I think the is a bit of ambiguity in the problem statement. I assumed that there was also artwork in the inner circle. Then there would need to be one guard in the center circle then leaving only three available for the outer circle. From that understanding, I solved the problem similarly to this solution only with the inner circle inscribed within a triangle rather than a square. Is there anything in the problem statement to suggest that the inner circle is empty?
Log in to reply
The floor plan is an annulus
This indicates that the inside of the inner circle isn't relevant, which is why we shaded it in black. Do you have any suggestions for improving the phrasing?
Log in to reply
No, I apologise-it was my mistake. I was envisioning a section of the art museum in my home town consisting of concentric circles. I forgot an annulus is solid in the center. Thank you for your response.
Marta, if you don't mind my asking, what software are you using to make your (excellent) diagrams?
Log in to reply
I use Microsoft Word. I print the word file to get .pdf file, then I go to PDFtoPNG.com to convert the .pdf file to .png, finally I use Paint to crop the result. It sounds time consuming, but it isn't, actually. The entire procedure is click, click, click. And Microsoft Word, with all of its problems, does make good pictures. I also write my solution first on Word, so I can save my files pictures, text, and all.
Where did you get that 2r^2 is it (2r)^2 or 2r^2 what formula is that?
Log in to reply
That's a Pythagorean theorem: r 2 + r 2 = 1 0 2 .
the right solution is: 10 sin(67.5)
(every part of the gallery must be visible to at least one guard)

Placing guards on alternate vertices of the octagon will give an optimal result if we want to guard only the outer circle. This configuration leaves some points unguarded on the inner circle. We would have decrease the radius of the inner circle so that the entire inner circle is guarded as well.
Your solution leaves 4 areas of the floor that are out of sight. Each blocked by the inner wall. Each guard needs to be able to see the 2 adjacent guards in order for there not to be any area invisible to any guard.
Log in to reply
Yes, this configuration requires a minimum of 8 guards. The inner circle needs to be smaller if we have only 4 guards.
4 regions out of sight!!!
But, as pranshu said some of the parts of annule remain uncovered so their answer is correct
Fawazi saldin....yep I did that only, Maximised radius is achieved when the line of viewpoints of guards become tangents to the circle..
A guard standing on the outer edge of the room can see a potion of the of the inner wall:
The angle x can be calculated using trigonometry (as the guard's line of sight is tangent to the inner circle), where R is the inner radius:
cos x = R 1 0
We want this angle to be as small as possible, as this will allow us the largest inner radius. Using the pigeon hole principle, at least one guard must see 3 6 0 / 4 = 9 0 ∘ . We therefore want angle x to be at most 4 5 ∘ . This gives us:
R = 1 0 cos x ≤ 1 0 cos 4 5 R ≤ 2 1 0
This is a theoretical maximum for the inner radius, but we haven't yet demonstrated that there exists a configuration of 4 guards that allows them to see an entire room where the inner radius is 2 1 0 .
The most efficient placement of the guards would be equally spaced around the outer circle, one every 9 0 ∘ . We want the guards to have no overlap in what they can see of the inner wall. This is achieved by having the inner circle tangent to the sides of the square formed by connecting our 4 guards.
The radius of the inner circle is therefore half of the side of this square, s
s 2 + s 2 = 2 0 2 s 2 = 2 0 0 s = 1 0 2
So, our inner radius is:
2 1 0 2 = 5 2
Which matches the theoretical maximum we discovered in the first part of the solution, and is therefore the best possible scenario.