Half Circle in a Triangle
Note: The semicircle is tangential to A B and A C . In particular, the endpoints of the diameter are not B or C .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
why they will be equal to r
Log in to reply
As the sides are tangent to the circle,line joining the center and the point of tangent will be perpendicular to the tangent and this line is nothing but the radius..I think now its all clear..
Log in to reply
is AB really tangent to the semi cirlce?...if yes then at wat point?
Log in to reply
@Pallavi D – yes. Because the circle is "inscribed in triangle" all sides are tagential to circle. And because radius is perpendicular to tangent at the point of contact, the root of perpendicular on AB from O is the point of tangency.
Log in to reply
@Sagar Kulkarni – if AB is a tangent to the semi circle then AB should be perpendicular to BC because BC is one of the diameter .
let, OB=r=OD(perpendicular to AC from O), so from two triangle ABO & AOD we get AB=AD(as radius is perpendicular to the tangent AB & AD). CD=AC-AD=14-10=4. (12-r)^2=CD^2 + r^2. i.e. r=16/3=5.33.......rest is all known _ _
but area of semicircle is pi rsquare/2
Assuming angle ABO as right angle is a wrong idea, as AC^2 != AB^2 + BC^2. Hence other calculations are wrong.
By cosinus law C=44° B=78° and A=57° M is the point on AC where the circle meets the triangle If we connet it to O (center of the circle) we have a rayon OM and OMC= 90°(tangenciel) Then COM = 45° (180-90+44) , then MOB = 133° (180-45) If we connect BM we have an isocele triangld MOB because of 2 rayons OMB=MBO=23° In the triangle AMB AMB = 66° (90-23) , MBA= 55° (78-23) By the sinus law BM = 9.14cm In the triangle MOB By sinus law MO=OB=4.90cm 0.5 Circle's aire = pi × R^2 × 0.5 A = 4.90^2 × 0.5 = 12cm
Great (y)
you are awesome!!!
Gud 1
The circle does not touch point B as can be seen. From the question it is clear that the half circle is inscribed in the the triangle. It does not say it passes at point B. Your solution is correct.
Is there another method then Heron's formula. Heron's formula is approximate value of area!!!
good
how point 'B' can be on the circle? as associated angle is not 90'.
how would AOC's area = AC.r/2 ??
how did you get 24pi from 24root6?
Brllliant. I went about it in a long winded way including angular bisector method
For clarity you should have added r=2root6
Whatdo you mean by it giesca cirle 24pi? :
thank u
GREAT
I tried to make this solution as detailed as I could.
Let trace the line that goes from O to the B C side of the triangle, forming 90º with the same. Automatically, this segment takes on the character of semicircle's radius.
Now, let trace the segment A O .
Therefore, the area of the triangle A B C is the sum of the areas of triangles A O B , A O D and O C D . Then, denoting the area a triangle A B C by [ A B C ] , we have:
( 1 ) [ A B C ] = [ A O B ] + [ A O D ] + [ C O D ]
Note that the triangles A O B and A O D are congruent by the case of three equal sides. So, we get:
( 2 ) [ A B C ] = 2 × [ A O D ] + [ C O D ] .
Calculating the area of the triangle A B C by the Hieron's formula,
[ A B C ] = p ( p − a ) ( p − b ) ( p − c ) , where p is the semiperimeter of the triangle A B C and a , b , c the sides. We have:
= 1 8 ( 1 8 − 1 2 ) ( 1 8 − 1 4 ) ( 1 8 − 1 0 )
So, [ A B C ] = 2 4 6 .
Denoting the radius of the semicircle by (\r), we have that he areas of the triangles (\AOD and COD) are, as a function of r :
( 3 ) [ A O D ] = 2 r × 1 0 = 5 r ,and
( 4 ) [ C O D ] = 2 r × 4 = 2 r .
Comparing the equations ( 2 ) , ( 3 ) and ( 4 ) , we get:
[ A B C ] = 2 4 6 = 2 × 5 r + 2 r
2 4 6 = 1 2 r
r = 2 6
Finally, calculating the area of the circle and comparing it to a π , we get:
A r e a = 2 π × r 2 = 2 π × ( 2 6 ) 2 = 2 π × 2 4 = 1 2 π
...Comparing,
a π = 1 2 π
So, a = 1 2
Q . E . D
This didn't make much sense to me. What does D represent in this solution? How are A O B and A O D congruent?
Log in to reply
AB=AD(two tangents to the half circle from the point A),BO=OD=radius,AO=AO. So triangles ABO & ADO are congruent.
great....
Log in to reply
How can we be sure that triangle ABO and triangle ADO are congruent. because if that is the case the angle B Should have been a right angle triangle and pythagorus theorem sould be satisfied in case of triangle ABC !! but thats not happening here
Log in to reply
true and if angle B is right angle then what is the use of herons formula???? we could have used 0.5 AB BC
Yes. I proved that it is false in a comment here. As this don't happen, you can use his proof for a approximate value of "a", not the real result
ok...wait...what???
great!
How did you get (3) and (4)???????????
AOB and AOD are not congruent. just that [ABC]=[AOB] + [AOC] and, [AOB]=0.5 AB.r [AOC]= 0.5 AC.r
fadu q
use cos rule twice.. you'll get it
how find area of (AOD)&(COD)
Log in to reply
line AC touch the circle at point D. AOD & COD is a right angle triangle & congruent using formula (1/2* bass* height)
fine
good. Area ABO + Area AOC= 1/2 10 r + 1/2 14 r =12 r =24 r =Area ABC. So r=2*6^1/2..Rest fine & A=12
Your idea is really good, but there is something wrong that I found in ALL the solutions that were given, and that actually makes the question wrong: OB IS EQUAL TO r! NOT POSSIBLE. That's simple to prove! If OB = r, Than ABC do a angle of 90 degrees (AB is tangent to the circle). So:
10^2+12^2 = 14^2
100 + 144 = 196
244 = 196 (not true)
The area that you used (ABC), should be actually changed to something like AEC. It will be a area A LITTLE smaller than ABC. So the answer must be approximately a, not equal to.
Log in to reply
thanx i was having confusion for that. now i cleared my doubt.
Triangles AOB & AOD are not congruent, because OD isn't equal OB. Od =r, but OB is not perpendicular to BA and doesn't touch circle at B. So, OB > OD. So, your solution is close to the correct, but it's incorrect.
We can reflect Triangle A B C over line B C to form Quadrilateral A B D C . Now label the points where the circle touches the quadrilateral, E , F , B , and H where E is between A and B , F is between B and D , G is between C and D and H is between A and C . Now since A E = A H , we have that A O an angle bisector. After applying angle bisector theorem, we have that B O = 5 and C O = 7. Now we apply Stewart's theorem to find that A O = 1 0 5 . Now let A E be x and and B E be y . Now we apply Pythagorean theorem on triangles A E O and B E O . Since both share a side length of r , we can set the two equations equal to each other. Thus, we have 1 0 5 − x 2 = 2 5 − y 2 . This can be rearranged into x 2 − y 2 = 8 0 . However, we know that A E + B E = A B , so x + y = 1 0 . Divided the first equation by the second yields x − y = 8 . Now that we have the two equations x + y = 1 0 and x − y = 8 , we can easily find that x = 9 and y = 1 .
Using Pythagorean theorem again, we find that r 2 = 2 4 . The area of our semicircle is 2 π r 2 so our answer is 1 2 .
I do not understand Brother?
This the correct method
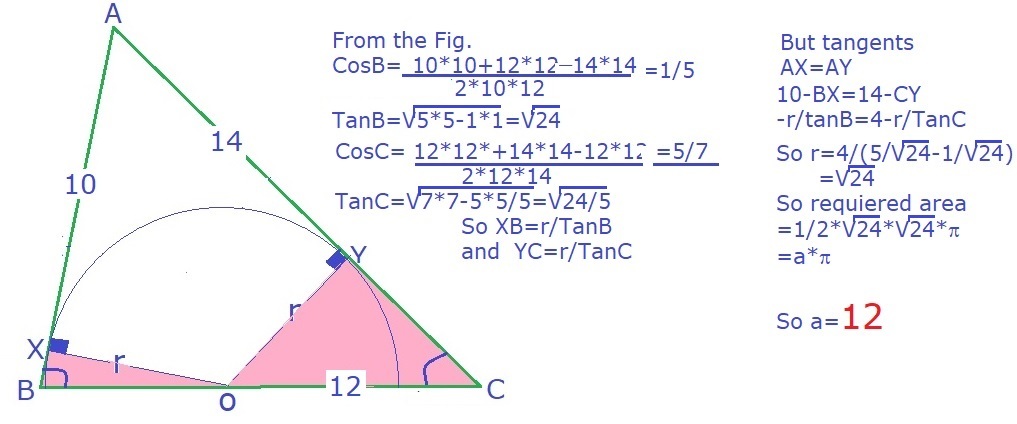
Thanks to Saloni Arora . It is his solution that leads to mine.
- Let radius of semicircle R.
- Using Cosine Law: cos B = 1/5 or sin B = (2/5)sqrt(6) ; cos C = 5/7 or sin C = (2/7)sqrt(6).
- From the figure, cos (90 -B) = sin B = R / BO, sin C = R / OC.
- Using algebra: BO + OC = 12 or (R / sin B) + (R / sin C) = 12, or R = 12 / sqrt(6).
- Area of semicircle = (1/2)(pi)(R^2), A = (1/2)(R^2) = 12. (Q.E.D.)
using cosine rule i.e a^2=b^2+c^2-2(b)(c)(cos@) where @=angle opposite to line a. taking a to be the line i.e 10 we solve this equation and find @ @=Cos^-1((144+196-100)/2(14)(12) so @=44.415 than as we know that when a tangent touches a circle it makes an angle of 90 with the line made from the centre of the circle. which happens when the line with lenght 14 touches the semicircle at an imaginary point x. we form a right angle triangle OXY where Yis the point where line 14 and 12 meet. than using sine rule i.e sina/a=sinb/b like this sin(44.415)/r=sin(90)/(12-r) where r=radius of circle we simplify the equation to 8.4-0.7r=r and get r to be equal to 4.94 than using formula area of semicirle= pi r^2/2 we equate Api=r^2/2 pi and we get A=12.2.
First of all, B doesn't touch circle ark. Point where semicircle touches BA is located on BA, but a little bit higher than point B. So, if join O with BA in point, let's it be E, it'd be right triangle BEO with side OE = r. On the other site lets join O with CA where circle touches CA in point, let's it be D. It makes right triangle ODB With OB = r. In order to find out r length it's needed to solve these triangles, just to find out sin(A) and sin(B) values. Knowing all 3 sides of ABC it's possible to determine cos(A) and cos(B) using cosines law:
cos(A) = (AC^2 +AB^2 - BC^2)/(2AC x AB) =(10^2 + 12^2 - 14^2)/(2 x 10 x 12) = 0.2, cos (A) = 0.2, A = 78.5 degrees, sin(A) = 0.98.
cos(B) = (AB^2 + BC^2 - AC^2)/(2AB x BC) = (12^2 + 14^2 - 10^2)/(2 x 12 x 14) = 0.784, cos(B) = 0.714, B = 44.4 degrees, sin(C) = 0.7
So, AO = r/sin(A), OB = r/sin(B), AB = AO + OB = r/0.98 + r/0.7 = 12. Solving this equation: 0.7r + 0.98r = 0.69 x 12, r = 8.28/1.68 = 4.9, Semicircle Area = (0.5r^2) x Pi =(0.5 x 4.9^2)Pi;
Answer: A = 0.5 x 4.9^2 = 12.(approximately).
1/2 πr² =πa r =√2a 10/14=(√2a+x)/(12-(√2a+x)), where x is difference of length of radius and gap of semicircle. Solve above equation considering x as negligibly small and calculate, a =12.5 if you consider value of x now we get ”a” less than 12.5 we get a=12 from option.
good understanding...
Drop the radius on AB and AC at points X and y respectively such that ∠BXO = ∠CYO= 90 degree. Let r be the radius of the circle. Now, in both these triangles BOX and CYO,
By cosine rule, cos B= (a²+c²-b²)/2ac
cos B= 1/5
sin B= 2√6/5
Also, by Pythagoras theorem, r/(12-y)= 2√6/5 (Here y is CO, thus BO= 12- y) .....eqn 1
Now in triangle CYO, by same cosine rule and pythagoras theorem,
r/y = 2√6/7 ....eqn 2
Solving eqn 1 and 2-
y=5 and r= 2√6
∏r²/2= a∏
and a= 12 (substitute r)
The solution looks much more easier if accompanied by a diagram alongwith, unfortunately we can't do that here
Yes, it work
How did you get the values of cos B & sin B????
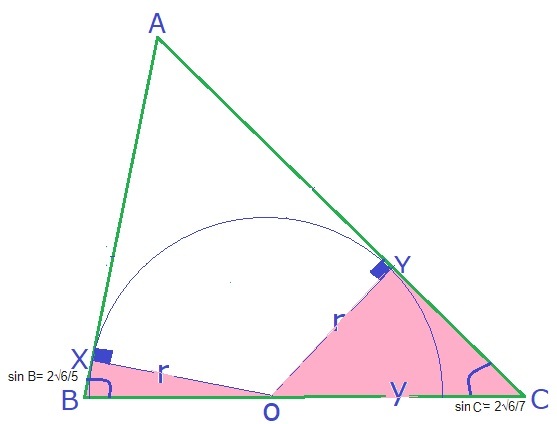
The diagram.
my way isn't very accurate but it worked
by heron's formula: area of the triangle is sqrt{18 * 8 * 4 * 6}= 24 sqrt{6}
Let's drop a perpendicular BD of height h from B on AC
drop another perpendicular OE from O on AC, it's obvious that OE= r
now triangles COE and CBD are similar then
CO/CB= OE/BD
let's assume that CO= 12-r "small part of BO on the left of the semi-circle is neglected"
CB=12
OE=r
BD= h=24/7 sqrt{6}
by substitution you get slightly larger value of r and the SA of semi-circle appears to be 12.204*pi
the closest answer is 12
Draw perpendiculars from O on side AB & AC. Say, they will intersect AB at D & AC at E. Evidently they will be the tangent points. So OD=OE=radius of the half circle.Now join A to O. Two triangles formed, AOB and AOC. Area of AOB=AB r/2 and for AOC=AC r/2. Sum of these two will be the area of ABC which is equal to root square of S (S-10)(S-12)(S-14).S=half perimetre of ABC. From this we can make an equation and find r. Now its easy to find the value of a. Ans is 12.
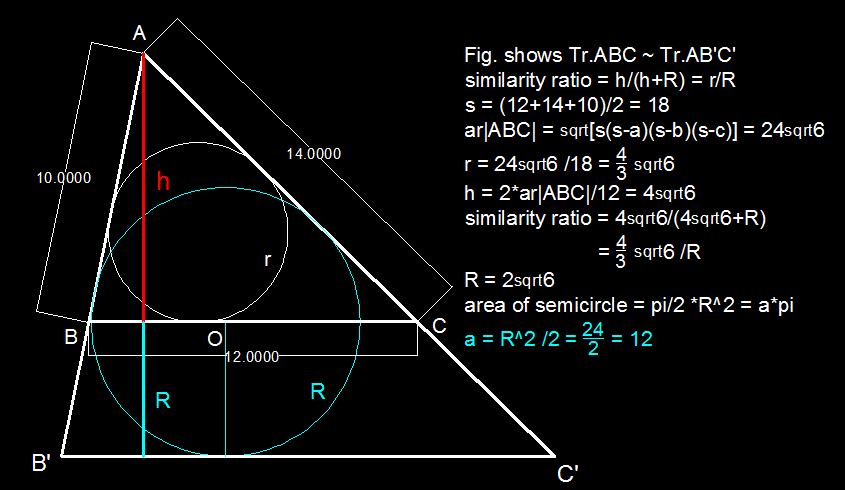
Join A and O.Drop a perpendicular from O to AB and to AC,they will be equal to r.Area of ABO = 2 A B . r similarly for AOC 2 A C . r .Adding this 2 areas give the area of whole triangle which is equal to 2 4 6 by Heron's formula.This gives area of full circle =24pi so half area=12pi.