Three point shot: the half-court heave

If the ball is to pass through the point $(d,h)$ , when projected at an angle $\alpha$ to the horizontal, then it has to be projected at speed $v_\alpha$ , where $h \; = \; d\tan\alpha - \tfrac{gd^2}{2v_\alpha^2\cos^2\alpha}$ If the ball is projected at this speed $v_\alpha$ at an angle of $\theta$ to the horizontal, its trajectory is $y \; = \; x\tan\theta - \tfrac{g}{2v_\alpha^2\cos^2\theta}x^2 \; = \; x\tan\theta - \frac{(d\tan\alpha - h)\cos^2\alpha}{d^2\cos^2\theta}x^2$ and so the ball passes through the points $(d,H(\theta))$ and $(D(\theta),h)$ where $\begin{aligned} H(\theta) & = \; d\tan\theta - (d\tan\alpha - h)\cos^2\alpha\,\sec^2\theta \\ h & = \; D(\theta)\tan\theta - \frac{(d\tan\alpha - h)\cos^2\alpha}{d^2\cos^2\theta}D(\theta)^2 \end{aligned}$ Measures of vertical and horizontal deviation for the shot are $|H'(\alpha)|$ and $|D'(\alpha)|$ respectively, and it is easy to calculate that $\begin{aligned} H'(\alpha) & = \; d + 2h\tan\alpha - d\tan^2\alpha \\ D'(\alpha) & =\; \frac{d(d + 2h\tan\alpha - d\tan^2\alpha)}{d\tan\alpha - h} \end{aligned}$ Thus the least possible horizontal and vertical deviation occurs by choosing $\alpha$ such that $D'(\alpha) = H'(\alpha) = 0$ , which can be done by solving $d\tan^2\alpha - 2h\tan\alpha - d \; = \; 0$ and hence (since $\tan\alpha > 0$ ) $\tan\alpha \; = \; \frac{h + \sqrt{h^2 + d^2}}{d}$ For this problem, this means $\alpha = \boxed{47.26733^\circ}$ .

I did some intuition. I knew that firing angle for the maximum range for a projectile is the bisector of the base line (whether down, level or up) and the vertical. Or the minimum firing velocity for a given range. As this is a maximum range $\frac{drange}{dangle}$ = 0. So this is likely to be the magic angle in the question. Thus directly the answer is 45°+ arctan(1.15/14.5)/2 = $\boxed{47.27°}$

Let $\theta$ be the angle of the shot from the player. Then, given gravitational constant $g$ , velocity of the shot $v$ , and letting $x$ be the distance from the player, the equation of the trajectory from the player's hands is

$y=Tan(\theta)x-\dfrac{g}{2v^2}(Sec(\theta))^2x^2$

Let's assume the ideal shot goes through the center of the rim at $(x,y)=(14.5,1.15)$ . Then we can determine the velocity to be

$v(\theta)=\dfrac {29\sqrt{5g}Sec(\theta)} {\sqrt{580Tan(\theta)-46} }$

Now, we're going to assume that the player will make that shot at that exact velocity but that there could be an error $\delta \theta$ in his angle of shot, so that we have (while keeping $v(\theta)$ exactly the same as before with no $\delta \theta$ )

$y=Tan(\theta+\delta \theta)x-\dfrac{g}{2v(\theta)^2}(Sec(\theta+\delta \theta))^2x^2$

Given $y=1.15$ , we solve for $x$ to get the function $x=f(\theta, \delta \theta$ ) of those variables. We wish to see, for a given shot angle $\theta$ , the deviation $\delta x$ we get from deviation $\delta \theta$ , so we differentiate $f(\theta, \delta \theta)$ with respect to $\delta \theta$ to get the slope function

$g(\theta,\delta \theta) = \dfrac{df(\theta,\delta \theta)}{d\delta\theta}$

and then we let $\delta \theta \rightarrow 0$ , or

$g(\theta,0)$

which we want to equal to $0$ for least variation $\delta x$ as a function of $\delta \theta$ . We determine the value of $\theta$ numerically to be $0.8349705028...$ radians, or $47.267328...$ degrees.

Comment: Mark Henning's approach is computationally much simpler to carry out. An upvote for his solution.

In this question, we ignored a few details that are surely important for making the shot (like the geometry of the rim) and imposed an unfounded assumption (that Curry would be aiming for the center of the rim). It's not clear from the outset whether the rim would fundamentally change the answer or if aiming at the center would necessarily be his best choice. In this solution, I'm going to skip the minimum deviation problem (already addressed by Mark and Michael), and consider how the geometry of the shot, coupled with small errors in shot velocity and angle, affect the answer if at all.

To start, we have $\begin{aligned} x(t) &= v_0t\cos\theta \\ z(t) &= z_0 + v_0t\sin\theta - \frac12 gt^2 \end{aligned}$

and by solving the horizontal equation for $t,$ substituting into the vertical relation, we have

$\Delta z(x) = x\tan\theta -\frac{gx^2}{2v_0^2\cos^2\theta}$

To find a more realistic notion of robustness, we can instead look for the minimum and maximum shot angles that will still result in a basket, given the corresponding shot velocity. Practically, this will yield two velocity-angle curves, and the area between them will correspond to made shots while the area outside will correspond to missed shots. For simplicity, we're going to use the two extreme cases shown below as the range of "made" shots, and will ignore shots that are made by bouncing upward off the rim or bouncing off of the backboard.

For any shot angle $\theta,$ there exist two shot velocities $v_\text{min}$ and $v_\text{min}$ that will result in the basketball hitting the target. In general, the shot angle can be as great at $\theta=\pi/2,$ but at the lower end, there exists a minimal angle $\theta_\text{min},$ realized at the angle where $v_\text{min} = v_\text{max}.$ This corresponds to the angle where the basketball just skims the front of the rim on the way into the basket.

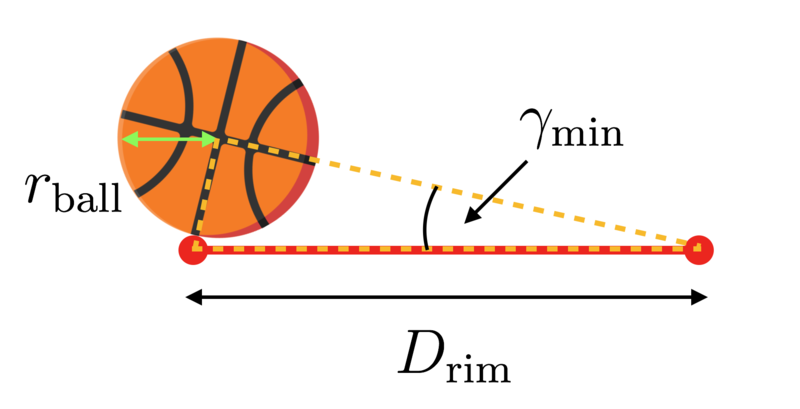
We can find the maximum velocity by setting the target value for $x$ to $d + D_\textrm{rim} - r,$ the location of the center of the ball when it hits the back of the rim at $\Delta z = h.$ Similarly, we can find the minimum shot angle by adjusting the target $x$ value to $d - \frac12 D_\text{rim} + r_\text{ball}\sin\gamma_\text{min}$ and the target $z$ value to $h + r\cos\gamma_\text{min}.$ (see diagram)

Plotting these two curves yields the graph below

This shows that the region with the greatest forgiveness in $\theta$ -error is near $\theta = \SI{47.3}{\degree},$ in basic agreement with the result of the simple minima condition from this problem. Interestingly, this overlaps with a region of roughly constant, maximal forgiveness in $v$ -error.

Zooming in a bit, we can pick up some more insight to shot selection.

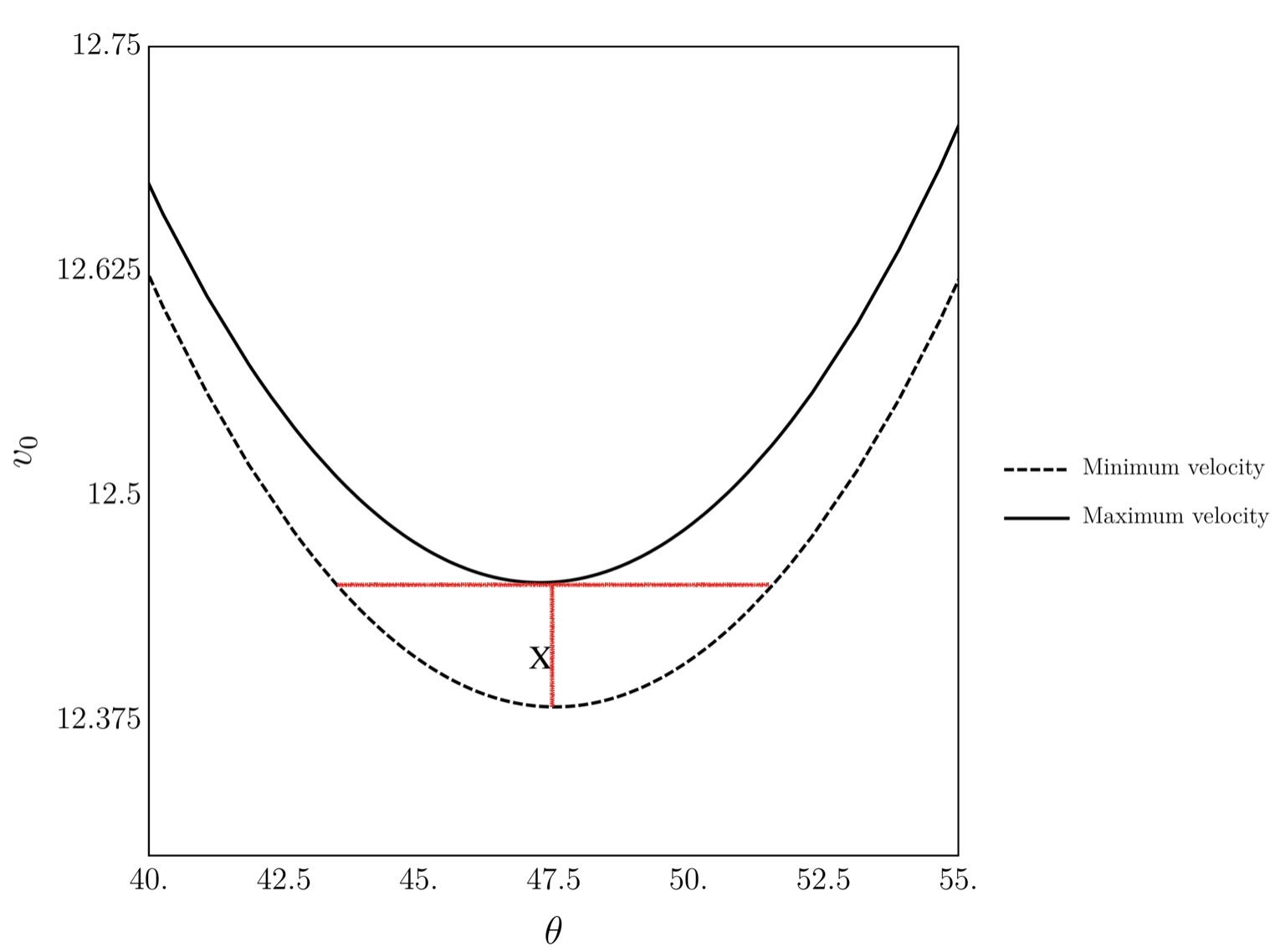
Inspecting this plot, we see that the shot angle around which there is maximal tolerance for errors is $\theta\approx \SI{47.5}{\degree}.$ But if we plot the $v$ and $\theta$ found from the technique recommended in this problem (shown as the "x" in the plot), we see that the shot velocity is too low. Had we chosen a higher shot velocity while keeping the same angle, we'd have greater two-sided tolerance for errors in $v.$

What this means physically is that it's not optimal to aim for the center of the basket, as we assumed Curry would in this problem. Instead shooters should aim for a point somewhere beyond the center of the basket, with the exact location determined by more sophisticated inspection of this kind of plot.

Selecting an optimal $v$ and $\theta$ for a given player is of course guided and constrained by this plot, but ultimately depends on the tendencies of the given player to errors in $\theta$ and $v.$ If a player is especially accurate in $\theta,$ it can be advantageous to move to a higher angle that allows more error in $v,$ while a player prone to error in $\theta$ would want to move down the curve.