Half Full or Half Empty?
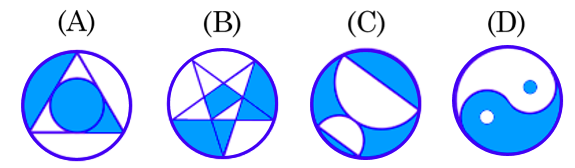Which of these circles is NOT half-shaded blue?
Bonus: can you prove that the rest are 2 1 and 2 1 , a couple are very tricky proofs!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
can u show how u prove a5 and b5 are similar?
Log in to reply
By angle chasing, the obtuse angle of A6 and B6 are 1 0 8 ∘ . A6 and B6 are clearly isosceles triangles (the small sides are sides of the regular pentagon), so the acute angles are 3 6 ∘ each. The vertex where A6, A5, B6 meets forms 1 0 8 ∘ angle. This leaves 3 6 ∘ for the small angle of A5. A5 is also isosceles (the long sides are diagonals of the regular pentagon), so A5 is isosceles with small angle 3 6 ∘ .
B4 is also isosceles with small angle 3 6 ∘ , and it shares the small side with A5. Thus A5 and B4 are congruent. Since B4 and B5 are also congruent, A5 and B5 are thus congruent.
Hao Zhe Loh Even if they aren't similar, the large amount of excess would still mean that logically it's not 50/50
Log in to reply
I would argue that the excess part has a π in its expression which cannot be covered.
The shaded area of all the other circles must be irrational as they involve curves/circles. Half of the area of the circle must also be irrational. Look at the little polygon in the middle of B. That is rational. Thus it cannot be involved in being half of the area of the circle. So the answer is B.
I understand what you are getting at but half the area of a circle does not need to be irrational. Consider a circle with radius of π 1 Then the area is 1
Log in to reply
Another way; even if the radius was transcendental (so that the area is an integer) that would mean that the area of any polygon with sides a function of that number would be transcendental. The point is, both the circular part and the polygonal part can't be algebraic, so the previous commenter is correct.
That was exactly what I was thinking! Too bad we dont have anything so far for proving the rest are 50/50.
A rational number plus an irrational number can be irrational, as there are many examples of that. So, I don't really see why the polygon affects the answer. Siva Prasad's diagram seems more helpful. I suggest drawing a line vertically from the top vertex of the star and mapping if there's more blue one side overall other than the white.
In D, if you replace the blue area with white and the white with blue, you get an identical figure. Thus each color is half the circle. In C, if you let the lower semi-circle get very tiny, the upper semi-circle approaches the size of half the inscribing circle.
Nice idea for C, but still does not constitute a proof, since we have to proof that resizing the inscribed half-circles will not affect the blue/white ratio.
Log in to reply
In C, since we are not given the sizes of the semi-circles, and there is no suggestion that the relative sizes of the semi-circles are relevant, we can make them any size we like. I choose to make the smaller approach zero.
Log in to reply
Because they haven't given the sizes to you doesn't mean you can choose them to be any size you like. They point is you have to show its true for all sizes.
Log in to reply
@Clement Moylan – By not containing any sizes, C itself is claiming the question applies to all sizes, and it exactly means we can choose any size we like. We don't have to prove anything about different sizes. The person who posed the question is inherently claiming that the question applies equally to all sizes.
Log in to reply
@Gary Popkin – I agree that the question applies to all sizes but Your approach does prove this only for the case where the smaller approaches zero radius (that still does not make it a bad idea, but it has to be somehow expanded to prove the whole thing). What about smaller being half the size of the bigger? If limits are the same, it does not imply that the actual values are always the same. Take for example x^2 and sin(x). They have the same limit for x->0, but they are definitely not the same - that is what I am pointing out.
I was lucky enough to imagine the colors as fluids to see how much they fill the circle. And I got it right first try.
A- Axis B- Allies