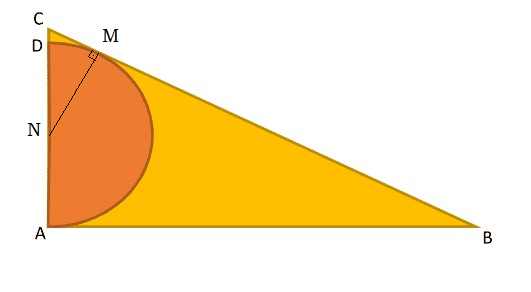
Half Inscribed
Given that A B = 1 2 , C D = 1 , ∠ B A C = 9 0 ∘ , and the semicircle is tangent to B C , find the radius of the semicircle.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
I think it would be good to specify ∠ C A B = 9 0 ∘ .
Log in to reply
what makes CMN similar to ABC? Because BC is a tangent to the semicircle?
Log in to reply
Because CMN is defined as the right triangle that includes the tangent point of the circle and angle ACB; angle NCM and ACB are the same angle, therefore triangle CMN and triangle ABC are similar triangles. (two angles in common means three congruent angles)
This works only if N is the centre of the circle ... how do we know this is so?
Log in to reply
What I meant to say is how do we know that AD is a diameter?
Log in to reply
If AC = 3 and AB is very large, then a circles centred on The mid-point of AD (N) does not touch CB
Log in to reply
@Brian Richards – AB is tangent to the circle at A. This means a radius of the circle that passes through A would be perpendicular to AB and vice versa. Since angle CAB is right, this implies the radius is on AC, so N must be on the side of the triangle.
wait how did you prove that tri-CMN is similar to tri-ABC?
Log in to reply
angle NMC is a right angle because point M is the tangent point to BC, and NM is a radius of the semicircle. Angle C is present in both triangles, which means they have two angles in common; by definition, two matching angles means they have three matching angles, so the triangles are similar.
Log in to reply
but what if the sides are different? I don't remember learning AAA to prove 2 similar triangles
Log in to reply
@Victor Ng – SAS proves congruent triangles. AAA is the definition of similar triangles that may still be congruent.
On what basis do you assume that the circle is tangent to CB? That is not a given of the problem as stated. Are you inferring that from the diagram? I think this problem provides insufficient data and I think that most of the solutions I see on this page make an unjustified assumption.
Log in to reply
It specifically says that BC is tangent to the semicircle.
Log in to reply
That was not true at the time I posted this comment. The question has been changed as a result of my report. Someone on the staff responded to my report "Thanks for spotting! I've updated the problem statement for clarity. I've marked this report as resolved."
Log in to reply
@Roger Neyman – If you make a solution comment that amounts to a report, and also make a report, you should delete your comment after the report is resolved. That would prevent people coming along afterwards and thinking you misread the problem.
Yes, Brian Egedy, It does state that BC is tangent to the semicircle. However, when originally published it did not. They added the qualification after my comment.
Same way I worked it.
Very good work, reading the comments I understood that sometimes is important to put some things clearer, but your soultion is totally right and there are no assumptions
Let M be the midpoint of A D and the center of the circle; let T be the point where the circle touches B C .
Then ∠ M T C = 9 0 ∘ = ∠ B A C , proving that △ M T C ∼ △ B A C .
The Pythagorean Theorem gives M C 2 = M T 2 + C T 2 ∴ ( r + 1 ) 2 = r 2 + C T 2 ∴ C T = ( r + 1 ) 2 − r 2 = 2 r + 1 .
Similarity gives the ratios T C A C = T M A B ∴ 2 r + 1 2 r + 1 = r 1 2 , which upon squaring becomes ( 2 r + 1 ) r 2 = 1 2 2 . This cubic equation is not easy to solve, but when we realize that Brilliant wants an integer value, it becomes obvious that r must be a divisor of 12, such that 1 2 / r is odd; this requires that r = 4 or r = 1 2 , and it is easy to see that only r = 4 works.
First I'd like to thank Mr. @Victor Paes Plinio for the image; it follows by Pythagorean Theorem on the triangle A B C that if we take x for the lenght of the segment M C and R for the radius of the circle
( 2 R + 1 ) 2 = x 2 + 2 4 x ,
given that A B = B M since both A and M are tangent points to the circle. Now, given the second right triangle M N C we have x 2 = 2 R + 1 . Feeding this information into the first result gives us the following equation for x :
x 4 − x 2 − 2 4 x = x ( x 3 − x − 2 4 ) = 0 .
If we want x = 0 we must solve a third degree polynomial equation. That can be done via Girard's relations, which will show you that the only real solution is x = 3 . Feeding it back into our equation relating x to R will result in
3 2 = 2 R + 1 ⇒ R = 4 .
Good use of Tangents concept here.
It never specifies that it's a half circle, it could be any amount of a semicircle and those statements could remain true, so the radius could actually be any positive real number
Log in to reply
semicircle
semicircle means exactly half of a circle. https://www.mathopenref.com/semicircle.html
I'm borrowed the diagram below from Victor Paes Plinio.
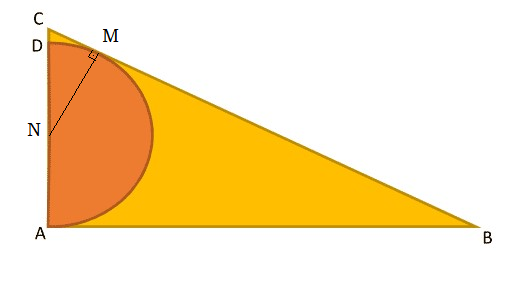
Let N be the center of the circle and r be the radius of the circle, then r = D N = A N = N M and A B = 1 2 ⟹ B M = 1 2 .
Let C M = x .
△ N M C ∼ △ A B C ⟹ r 1 2 = r + 1 1 2 + x ⟹ x = r 1 2
For △ N M C the Pythagorean theorem ⟹ ( r 1 2 ) 2 + r 2 = ( r + 1 ) 2 ⟹ 2 r 3 + r 2 − 1 4 4 = 0 ⟹ ( r − 4 ) ( 2 r 2 + 9 r + 3 6 ) = 0 ⟹ r = 4 , r = 4 − 9 ± 4 3 2 3 i .
Since r must be real and positive ⟹ r = 4 .
seeing AB = 12 makes us think of a (5,12,13) right triangle. Another is (9,12,15). Seeing if it is 9,12,15 we find the radius is 4. this works with the formula rs=a if ABC is turned into an isosceles triangle with ABC flipped over. Checking the 5, 12, 13 we get the radius is 12/5 which is incorrect and does not fit the shape. Therefore the radius is 4.
This is basically guessing the answer and confirming it, possible given the easy numbers. I could have picked a lot worse ones, though.
Log in to reply
Its taking advantage of the problem. If the numbers are weirder you would have to use more rigorous calculations but that's not the case and you shouldn't do whats more than needed for a problem.
Why must the radius be an integer (of 4)? Why can't it be 3.5? Or 3.8? Or π ?
correct answer is (25^2/3 -1)/2
(not considering negative and complex solutions we end up with 4)
Solutions that are only one equation are quite elegant !!
Triangle ABC is a 3-4-5 right triangle. Since side AB is 12 units long (3x4), side AC must be 9 units long (3x3), and DC=1, so the diameter of the semicircle is 9 - 1 = 8 = 2r, so r = 4.
That’s how I did it! I am shocked at how hard everyone else worked at this!
Having guessed that ABC is a 9-12-15 right triangle, you need to check that the circle of radius 4 centered at (0,4) is actually tangent to the hypotenuse. This turns out to be easy, since the tangent line to the circle through vertex C must form a right triangle with a leg of length 4 and a hypotenuse of 5, and thus the other leg has length 3, and so the angle at vertex C is the same as for the original triangle.
Some further work is required to show that this is the only radius of circle that works.
What information in the question tells you it's a 3-4-5 triangle?
Again, how can you determine that the triangle is a 3-4-5 triangle?
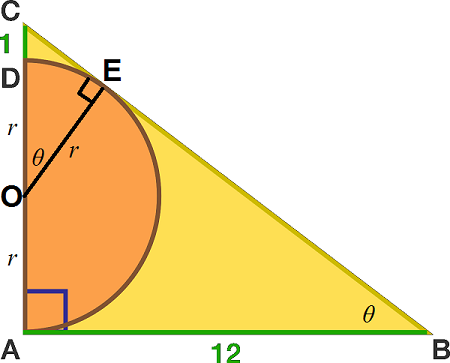 Let the center of the semicircle be
O
, its radius be
r
and the foot of the perpendicular from
O
to
B
C
be
E
. We note that
△
A
B
C
and
△
E
O
C
are similar. From
△
A
B
C
, we have
tan
θ
=
1
2
2
r
+
1
and from
△
E
O
C
,
cos
θ
=
r
+
1
r
. Then, we have:
Let the center of the semicircle be
O
, its radius be
r
and the foot of the perpendicular from
O
to
B
C
be
E
. We note that
△
A
B
C
and
△
E
O
C
are similar. From
△
A
B
C
, we have
tan
θ
=
1
2
2
r
+
1
and from
△
E
O
C
,
cos
θ
=
r
+
1
r
. Then, we have:
tan θ sin θ sin 2 θ sin 2 θ + cos θ = 1 2 2 r + 1 = 1 2 2 r + 1 cos θ = ( 1 2 2 r + 1 ) cos 2 θ = ( ( 1 2 2 r + 1 ) 2 + 1 ) cos 2 θ
⟹ ( ( 1 2 2 r + 1 ) 2 + 1 ) cos 2 θ ( ( 1 2 2 r + 1 ) 2 + 1 ) ( r + 1 r ) 2 4 r 4 + 4 r 3 + 1 4 5 r 2 4 r 4 + 4 r 3 + r 2 − 2 8 8 r − 1 4 4 ( r − 4 ) ( 2 r + 1 ) ( 2 r 2 + 9 r + 3 6 ) ⟹ r = 1 = 1 = 1 4 4 r 2 + 2 8 8 r + 1 4 4 = 0 = 0 = 4 Note that cos θ = r + 1 r Since r > 0
I don't know how I did this, but I visualised the BC tangent being at 1/3 the circumference, 1/3 of 12 is 4.
I think, there is a mistake/unclarity. It's nowhere said that the semicircle touches A. It's shown, yes, but never trust a picture ;)
It is specified that there is a tangent.
Thank Mr. @Victor Paes Plinio for the image.It's easy to find
M
N
C
M
=
A
B
C
A
. We can get this equation
r
2
r
+
1
=
1
2
2
r
+
1
.
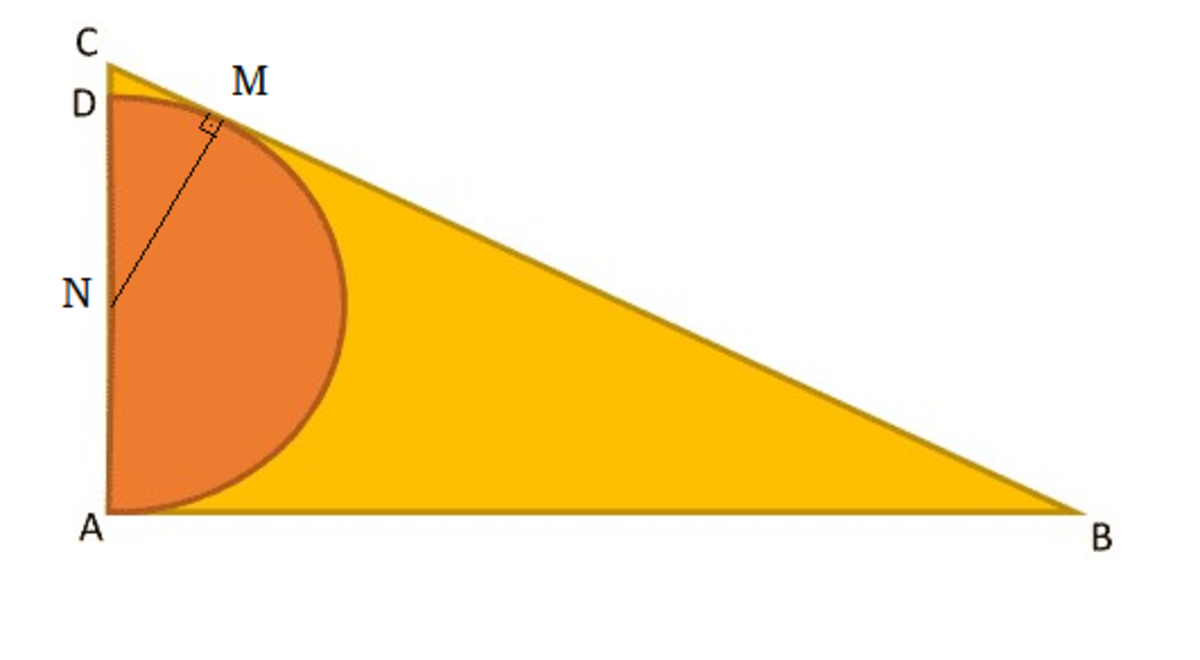 Let's do this replacement:
t
=
2
r
+
1
. Sort out the equation,then we have:
t
(
t
+
1
)
(
t
−
1
)
=
2
4
Let's do this replacement:
t
=
2
r
+
1
. Sort out the equation,then we have:
t
(
t
+
1
)
(
t
−
1
)
=
2
4
It is easy to see that a solution of this equation is t = 3 ,which means x = 4 .
When t > 0 , x > 1 , f ( t ) = t 3 − t increase monotonously. So x=4 is the only solution.
Why do you think that the answer is 7.5?
7.5 is the diameter, not the radius
Log in to reply
If you think that the answer is wrong, please defend your argument.
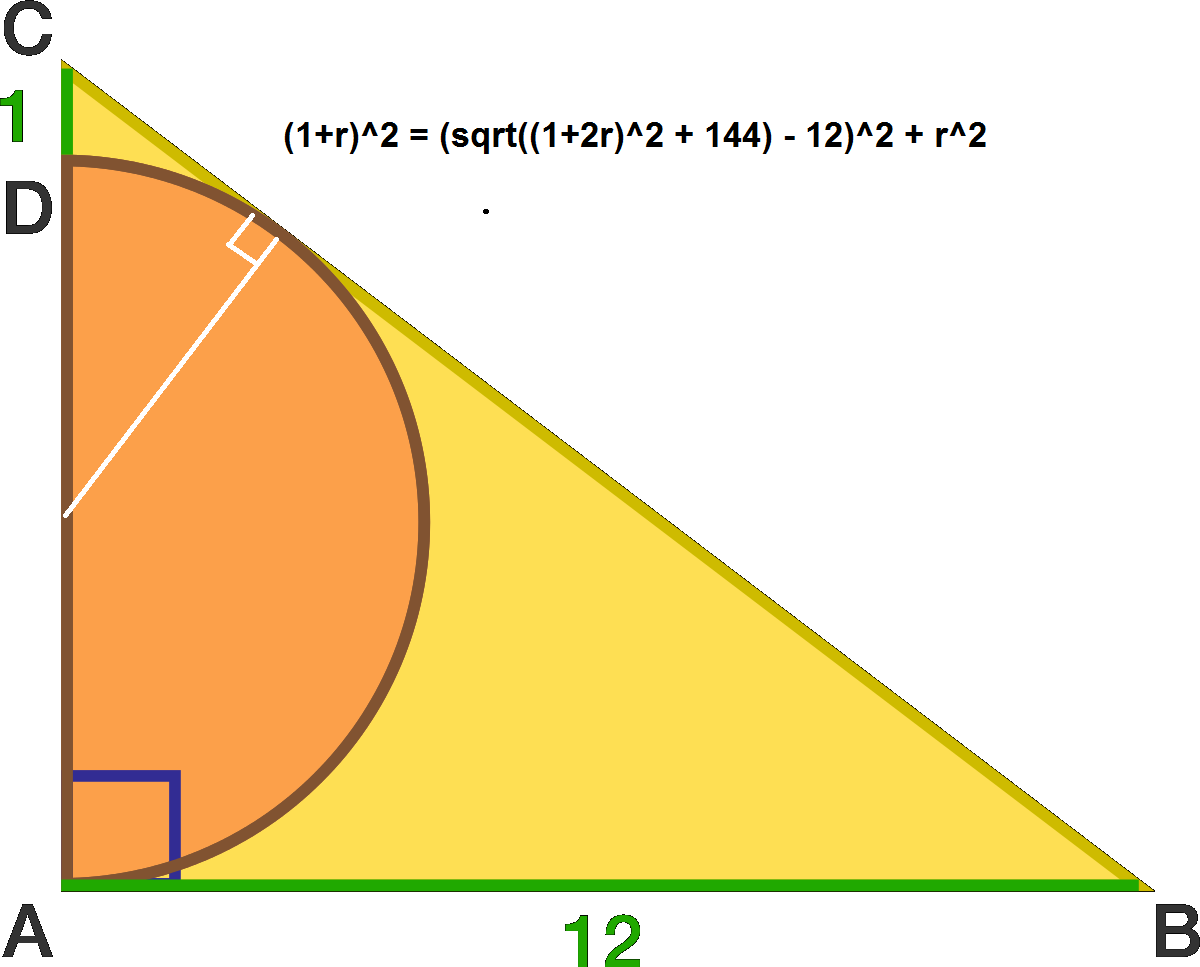
Let's call the radius of the semicircle as r . The length of A C is 2 r + 1 . The length of B C is, by Pythagorean Theorem, ( 2 r + 1 ) 2 + 1 2 2 = 4 r 2 + 4 r + 1 4 5 .
Look the image bellow:
The triangle C M N is similar to the triangle A B C . Then we have:
r + 1 4 r 2 + 4 r + 1 4 5 = r 1 2
Solving this equation we get:
x = 4 or x = − 2 1 or two others complex solutions. The only possible solution for the problem is x = 4