Half of Semicircle ? Or maybe not...

Geometry Level 2

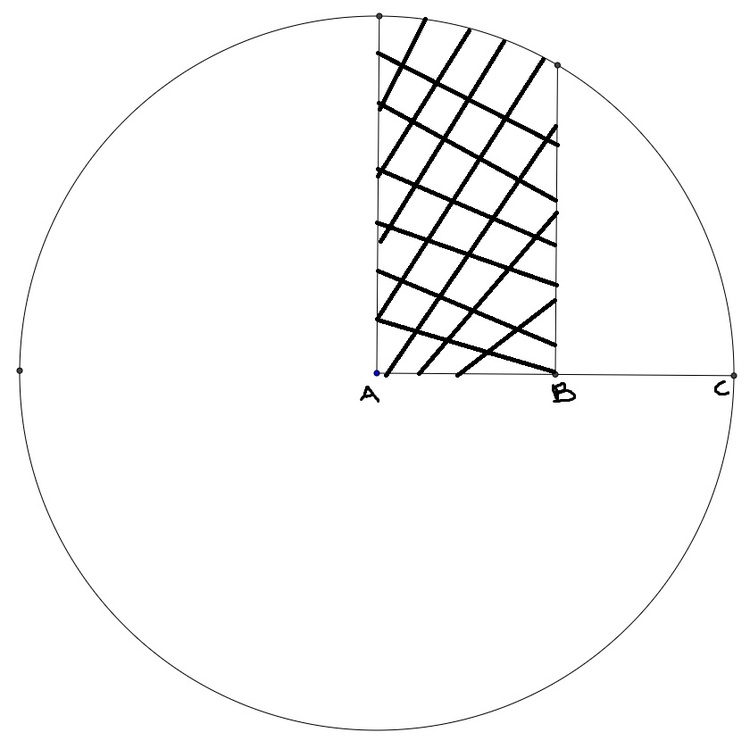Knowing that the radius of the circle (R = 1) and B is the middle of AC, find the area of the shaded region.

Answer is up to 3 decimals places.

The answer is 0.478.

4 solutions

Omkar Kulkarni
Jan 25, 2015

Let the point directly above $A$ be $X$ , and the one next to it be $Y$ . I'm gonna assume that $\angle XAC = \angle YBA = 90^{\circ}$ .

Now, the construction is joining $YA$ . Since the radius of the circle is $1$ , $AB=BC=\frac {1}{2}$ and $YA = 1$ . So, in $\Delta ABY$ ,

$\cos(\angle YAB) = \frac {1}{2} \Rightarrow \angle YAB = 60^{\circ}$ .

And hence, $\angle XAY = 30^{\circ}$ .

Now all we need to do is find the areas of sector $A - XY$ and $\Delta YAB$ and then add. The answer comes to be $\frac {\pi}{12} + \frac {\sqrt{3}}{8} \approx \boxed {0.478}$ .

well done sir, but I think the easiest way to do this is to take the $\int_0^\frac{1}{2} \mathrm{\sqrt{1-x^2}} \mathrm{d}x$

Radinoiu Damian - 6 years, 4 months ago

Oh okay. I don't know anything about calculus, so

Omkar Kulkarni - 6 years, 4 months ago

I did the same thing as you did. Though using integral is also a good way. It depends on how you want to approach it, either simple geometry or calculus

Nguyen Tra - 6 years, 4 months ago

Might be a typo in your second last sentence Triangle EAB, which is triangle YAB. Also Since you haven't mentioned the steps/formula used to calculate area of triangle YAB here it is: Sine rule can be used to calculate length of side YB, and then use that as height and the base AB , of the triangle YAB to find its area.

Ajit Deshpande - 6 years, 4 months ago

Oh yeah. By the way, you could directly use the formula $\frac {1}{2} ab \sin \theta$ to find the area.

Omkar Kulkarni - 6 years, 4 months ago

proof it.....please sir

Bhupendra Mahto - 6 years, 4 months ago

@Bhupendra Mahto – In $\Delta YAB$ , $\angle YAB=60^{\circ}$ , $AY=1$ and $AB=\frac{1}{2}$

Hence the area is $\frac{1}{2}ab\sin\theta=\left(\frac{1}{2}\right)(1)\left(\frac{1}{2}\right)(\sin 60^{\circ})=\frac{\sqrt{3}}{8}$

Omkar Kulkarni - 6 years, 4 months ago

we can use this formula 1/4th of area of circle - 1/4 th of area of ellipse

Umang Dubey - 6 years, 4 months ago

Mark the other points just above A and B as O AND P Join OC . Let it meet PB at X ...then Plzz point what is wrong if any in this solution. Why the answr cming is different ? 1st - area of trapezium OXBA

By Midpoint theorem, XB=1/2 OA = 1/2

By using formula Area comes as $\frac{3}{8}$

Now we clearly see that angle OXP = angle BXC =45

Area of part XOP = $\frac{45}{180}$ * area of segment OC

Ar(sgmnt OC ) = $\frac{pie}{4}$ - $\frac{1}{2}$ = $\frac{pie-2}{4}$

Area of part XOP = $\frac{pie-2}{16}$

Requird area = $\frac{3}{8}$ + $\frac{pie-2}{16}$ = $\frac{pie+4}{16}$

= $\frac{7.14}{16}$ = 0.446

tanmay goyal - 6 years, 4 months ago

Area of part XOP = $\frac{45}{180}$ * area of segment OC

Could you explain this step?

Omkar Kulkarni - 6 years, 4 months ago

By mid point theorem, OC is bisected at X

X is the centre of the chord making the segment OC ... I thought angle subtended by one arm of OC and a line joining X to a point on the segment , can be taken as a representative of the part it makes of the segment ...then i did wht we do in circles to find the area ..

$\frac{subtended angle}{complete angle=360}$ * area of circle ..

Here we see cmplte angle is 180..

I guess this way to find the ratio of parts of a segment acceptable...

Wht do you think?

tanmay goyal - 6 years, 4 months ago

@Tanmay Goyal – Ohh. No, you can't do that. The subtended angle has to be the angle subtended at the centre, and that is the segment whose area you get.

But if you did have to find the area of a portion similar to $\Delta OPX$ , you could maybe join points to the centre to form a segment whose area you could find by the formula. Just thinking aloud. This part has nothing to do with the problem. :P

Omkar Kulkarni - 6 years, 4 months ago

@Omkar Kulkarni – Dear ..I typed the frmula for circle only ..to illustrate its use in a segment ..

jst draw a segment of a circle frmd by a chord with centre Y(of the chord)

nd tell me if you are told 2 find how much a part formed by one arm of the chord nd a line segment with one point as Y and the other one smwhere on the arc making an angle x , makes of the whole segment ,

What would you do?? I m nt getting the option the option to insert an image in the reply ...else i cud 've illustrted better

tanmay goyal - 6 years, 4 months ago

@Tanmay Goyal – Oh okay I get you. I don't know how you'd find that.

Omkar Kulkarni - 6 years, 4 months ago

@Omkar Kulkarni – I did

$\frac{ area subtended at the centre of the chord }{180}$ * segmnt area

Here it i (45/180)* sgmnt area

tanmay goyal - 6 years, 4 months ago

The issue is that $OXY$ is not a circular sector. Note that $\frac{ \sqrt{2}} { 2} = OX \neq XY = \frac{ \sqrt{3}} { 2} - \frac{1}{2}$ .

Calvin Lin Staff - 6 years, 4 months ago

@Calvin Lin , Sir then can u plzz tell me how to find the ratio of the parts of a segment of a circle when the centre of the chord which has formed it nd the angle enclosed by 1 arm of the chord nd the line sgment with 1 point as the centre nd the other smwhere on the arc enclosing an angle x , are given .

tanmay goyal - 6 years, 4 months ago

@Tanmay Goyal – If you know that the arc is part of a circle, then the easiest way would be to break it out into the triangle and the tiny circular part.

This is essentially what was done, by looking at the sector $AXY$ which contains the circular part that we're interested in.

Calvin Lin Staff - 6 years, 4 months ago

@Calvin Lin – By the way Sir , how to attach n image in the reply

tanmay goyal - 6 years, 4 months ago

Plzz point out the fault if any in the solution i upvoted nd if there is none then clarify plzz why the answr cming is diferent?

tanmay goyal - 6 years, 4 months ago

Roman Frago
Feb 1, 2015

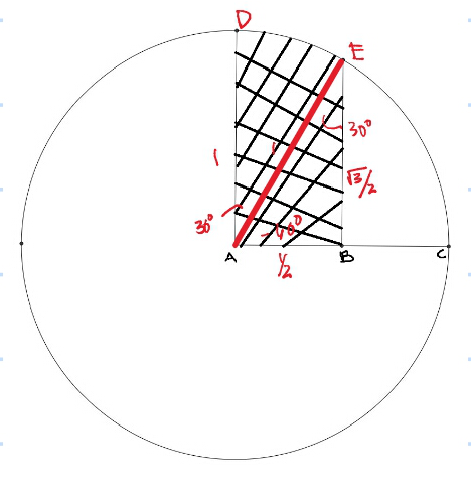
First, I assume the following: A is the center of the circle; The 2 line segments are parallel and are perpendicular to AC. Now, consider the image above.

$Area=(\frac {1} {2})(\frac {\sqrt {3}} {2})(\frac {1} {2})+(\frac {30} {360})(π)(1^2)$

$Area=0.478$

Gamal Sultan
Jan 31, 2015

Pi/4 - (1/4)(2Pi/3 + sin120) = 0.4783

Zakaria Sellami
Jan 31, 2015

I cheated by calculating the area of the shaded region as a trapezoid :p

yeah, but if you do it like that you're going to get a smaller area which is approx 0.466

Radinoiu Damian - 6 years, 4 months ago

Half of Semicircle ? Or maybe not...

The answer is 0.478.

4 solutions

0 pending reports