Half root (corrected)
Let f : R + → R + be a positive, monotonically increasing function with the property f ( f ( x ) ) = x . What is the value f ( 2 ) ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
As Aloysius points out in the comments, an explicit description of such a function is:
For
0
<
x
≤
1
,
f
(
x
)
=
x
2
2
.
For
x
>
1
, repeatedly take the square or the square root till we get a value
a
∈
[
2
,
4
)
. So,
x
=
a
2
p
for some integer
p
.
If
a
∈
[
3
,
4
)
, then define
f
(
a
2
p
)
=
(
a
−
1
)
2
p
.
If
a
∈
[
2
,
3
)
, then define
f
(
a
2
p
)
=
(
a
+
1
)
2
p
−
1
.
Then, if follows that f ( f ( a 2 p ) ) = a 2 p − 1 , thus f ( f ( x ) ) = x . In particular, this gives us f ( 2 ) = 3 .
Side note: There are several monotonic solutions to f ( f ( x ) ) = x + 1 , which echos the "pairing can occur arbitrarily".
Currently, I'm not too sure that that we must have f ( x ) = x 2 2 as the only solution to this problem. Let me think about it today.
Log in to reply
Yeah, there are other solutions, as I've added in the solution. This question is flawed. Perhaps we should add differentiable to the function.
Log in to reply
Yes, I've come to the same conclusion. At one point I thought I had proven that the proposed function, let's call it F ( x ) = x 2 / 2 , is the only possible solution. But as I was prepared to post the proof, I realized that I had a hidden assumption, namely that f doesn't cross F an infinite number of times in a neighborhood of x = 1 .
Pick any a > 1 and let b = F ( a ) . Define f on the interval [ b , a ] to be any desired monotonically increasing function such that f ( b ) = F ( b ) and f ( a ) = F ( a ) .
Then use the property f ( f ( x ) ) = x to define f on the intervals [ F ( b ) , b ) and ( a , F − 1 ( a ) ] .
And so on.
Log in to reply
@Peter Byers – Yeah, so this question can be established to be flawed.
I don't think requiring differentiability would make a difference. In fact, I believe there are alternate solutions that are smooth (but not analytic) functions.
Log in to reply
@Peter Byers – So the second approach to Markus' solution is still flawed potentially...
Do the other solutions match the given curve? With a graph provided in the question, surely there must be a unique solution (to 2 dp)?
Log in to reply
No, they do not. The picture is just an example, but there can be a variety of possible functions that satisfy.
Log in to reply
@Sharky Kesa – Sorry, but I don't think it's reasonable to dismiss the graph as 'just an example' when that's not indicated by the author. Questions often have information that is not given in word form. More than that, this question appears to be directly referring to the graph provided (showing a point of intersection).
Log in to reply
@Ben Greenfield – I absolutely agree with you! That's what I'm trying to tell him all the time! However, he insistently rejects my arguments!
@Ben Greenfield – The question would then say, "Use the diagram provided" or "Drawn to scale" or something. These sorts of assumptions should never be made. If you do that in a contest, you will likely get penalised (or even nullified) for doing such a thing, unless it is explicitly stated.
Log in to reply
@Sharky Kesa – All right, but you have missed the point, because something holds true for some types of graphs! Here, nothing is strictly specified, so that's why one can rely on some assumptions, as you did, trying to find a solutions! The result I have obtained implies those kind of graphs!
Hi Sharky, thanks for the insight! This is super cool :) At the moment I'm still trying to figure out how one goes out deriving that x = 1 is the fixed point from f ( x ) = f ( x ) . Would appreciate any pointers (or a formal proof would be super nice too)! Thanks!
Log in to reply
If you look at Markus solution, you can prove that f ( 1 ) > 1 and f ( 1 ) < 1 will lead to contradictions. Hence f ( 1 ) = 1 .
According to the definition, for x > 1 we conclude x < f ( x ) < x . If we assume f ( x ) > x , then x = f ( f ( x ) ) > f ( x ) > x , which is not true. Also, if f ( x ) < x , then x = f ( f ( x ) ) < f ( x ) < f ( x ) , and that is a contradiction. If one carefully has a look at the offered picture (unfortunately there is no option for the picture to be attached here in the comment! ), the problem is smply solved by the principle of golden ratio, i.e. if a > b > 0 , then a a + b = b a = φ . Just to describe the picture (providing that f ( x ) is continuous and its graph is of the shape as presented), the longest red line is extended up to the intersection with the line. Then, in this point set a parallel to the axis x , then extend the short red line up to the intersection with that line. In this way you've got a rectangular. Here a = x − f ( x ) , b = f ( x ) − x . So, since from a 2 − a b − b 2 = 0 there follows φ 2 − φ − 1 = 0 , its solution is φ = b a = 2 1 + 5 . Here f ( x ) − x x − f ( x ) = 2 1 + 5 , and for x = 2 , we obtain f ( 2 ) = 3 + 5 4 + 2 + 1 0 ≈ 1 . 6 3 7 9 6 . As for the golden ratio, please refer to https://en.wikipedia.org/wiki/Golden_ratio
Log in to reply
The golden ratio doesn't follow at all... You just got really lucky (or unlucky now, the answer is Cannot be Determined).
Log in to reply
The golden ration does follow, but there is no option for the picture to be attached here in the comment! It is modified picture you have given! Just to describe it, the longest red line is extended up to the intersection with the line y = x . Then, in this point set a parallel to the axis x , then extend the short red line up to the intersection with that line. In this way you've got a rectangular, further follow what I have written. This is the only logical approach, when you deal with a function defined in such a way, provided with no much information. Otherwise, it is just an artificial construction based on insufficient information! What you had in mind when creating the problem is one thing, possible consequences are another. The fact I have obtained a solution isn't matter of being lucky, but a quite rational reasoning in the existing circumstances! Do you really think that obtaining this result is a pure luck?
Log in to reply
@A Former Brilliant Member – Yes I do, as your logic does not follow.
Log in to reply
@Sharky Kesa – Yes, it does, because, it is just one way of approaching, since the problem wasn't precisely defined (as you are quite aware of), so one has to be open-minded for different kind of reasoning, especially if something doesn't fit into one's concept of viewing things!!! I'm so sorry if you can understand and accept that! The result 1 . 6 3 7 9 6 is such that it can't be a pure luck, if you are willing to think a little bit about that! Anyway, you have to be happy that a simple geometrical approach occurred to someone to solve a problem in analysis!
Log in to reply
@A Former Brilliant Member – Ok, I found the error in your working. How did you get a 2 − a b − b 2 = 0 ?
Log in to reply
@Sharky Kesa – I explained in previous comment. There is no possibility to attach a picture, but I described it. I repeat: Just to describe the picture (providing that is continuous and its graph is of the shape as presented), the longest red line is extended up to the intersection with the line. Then, in this point set a parallel to the axis, then extend the short red line up to the intersection with that line. In this way you've got a rectangular. If you know how I can attach the picture here, tell me!
Log in to reply
@A Former Brilliant Member – No, I know how you got to that step, but how do you derive from a = x − f ( x ) , b = f ( x ) − x that a 2 − a b − b 2 = 0 ?
If you expand it out, you get a 2 − a b − b 2 = ( x − f ( x ) ) 2 − ( x − f ( x ) ) ( f ( x ) − x ) − ( f ( x ) − x ) 2 = x 2 − 2 x f ( x ) + f ( x ) 2 + x f ( x ) − x x − f ( x ) 2 + x f ( x ) + f ( x ) 2 − 2 x f ( x ) + x = x 2 + x − ( x + x ) f ( x ) + f ( x ) 2 = 0 .
Nice edit, changing the comment's content completely.
Log in to reply
@Sharky Kesa – From the picture, the golden ratio is a a + b = b a , there follows a 2 − a b − b 2 = 0 . Afterwards, we find b a = 2 1 + 5 . Then we change a = x − f ( x ) , b = f ( x ) − x . Replacing x = 2 , we obtain the result. So for that kind of definition of graph you can obtain different values.
Log in to reply
@A Former Brilliant Member – How do you know from that picture that a a + b = b a ??? The picture doesn't show that at all...
Log in to reply
@Sharky Kesa – Yes, it does, when you modify the picture by adding and extending some red lines, you can see that! It would be good if there were a way to send you this picture! Perhaps you can send me you e-mail?!
Log in to reply
@A Former Brilliant Member – Ok, so you've said that a a + b = b a = φ where a = x − f ( x ) and b = f ( x ) − x . Let's compute using the trivial solution which is f ( x ) = x 2 2 , and we have x = 2 and f ( x ) = 2 2 2 ≈ 1 . 6 3 2 5 . (Well, your answer gives f ( 2 ) ≈ 1 . 6 3 7 9 6 and not ≈ 1 . 6 3 2 5 so there's something already a little off here)
a a + b = 2 − f ( 2 ) 2 − 2 ≈ 1 . 5 9 4 1
b a = f ( 2 ) − 2 2 − f ( 2 ) ≈ 1 . 6 8 3 2
φ ≈ 1 . 6 1 8 0
Clearly there's something wrong with your working (maybe you were only going for an approximation).
Also, someone has already given an example where f ( 2 ) = 3 ≈ 1 . 7 3 2 1 .
Log in to reply
@Ken Gene Quah – I've tried telling him, but he doesn't listen. He refuses to believe that he has made an error.
@Ken Gene Quah – It doesn't have to be only f ( x ) = x 2 2 ! It's just one of the functions, because the problem isn't strictly specified!
Log in to reply
@A Former Brilliant Member – Sharky and Ken's point is simply that your initial claim of " f ( x ) − x x − f ( x ) = 2 1 + 5 " is unfounded because there is no reason why that rectangle must satisfy the golden ratio even though it "looks nice in the picture". As a further substantiation, neither the function f ( x ) = x 2 2 nor the function that Aloysius defines satisfies this equation, which precisely indicates that it is not valid.
If you disagree and think that your equation is valid, please substantiate why it must follow the golden ratio, instead of just claiming that it does.
Anyone can find an example different function of f?
Log in to reply
Oh sure! However, I'm not used to using x , so I shall use g ( x ) , the inverse of f ( x ) . Then g ( g ( x ) ) = x 2 .
Consider the following definition of g(x):
g
(
1
)
=
1
,
g
(
x
)
=
x
2
when
0
<
x
<
1
.
g
(
a
2
p
)
=
(
a
+
1
)
2
p
if p integer and a in interval [2,3)
g
(
a
2
p
)
=
(
a
−
1
)
2
p
+
1
if p integer and a in interval [3,4)
Then f(2)=x if g(x)=2. This is when g= 3 . So in this function, f ( 2 ) = 3
Log in to reply
Oh wow, that's very nice! I wasn't expecting a simple functional form like this.
Side note: We should show that for
x
>
1
, there is a unique way to represent
x
=
a
2
p
where
a
∈
[
2
,
4
)
. That is almost obvious by squaring / rooting
x
as needed till it in is in that range.
We can generalize the function to
a
in the interval
[
b
,
b
2
)
. Namely, define
g
(
x
)
=
x
2
when
0
<
x
≤
1
g
(
a
2
p
)
=
(
a
+
2
b
2
−
b
)
2
p
where
p
is an integer and
a
∈
[
b
,
b
+
2
b
2
−
b
)
.
g
(
a
2
p
)
=
(
a
−
2
b
2
−
b
)
2
p
where
p
is an integer and
a
∈
[
b
+
2
b
2
−
b
,
b
2
)
.
And, if we really really wanted, we could do the same for 0 < x < 1 , where we pick a 0 < c < 1 , and use the boundaries of ( c 2 , c ] .
@Markus Michelmann In this case, you can clearly see that the function f = g − 1 is not differentiable at x = 1 , because of the "kinks" at the boundaries. However, the function is continuous, and differentiable almost everywhere.
First approch: If we assume a power function f ( x ) = c ⋅ x α it follows f ( f ( x ) ) ⇒ α = c ( c x α ) α = c 1 + α ⋅ x α 2 = x = x 1 / 2 = ± 2 1 , c = ± 1 We yield a positive, monotonic increasing function only if both signs are positve. Therefore, we get the result f ( 2 ) = 2 1 / 2 = 2 2 ≈ 1 . 6 3 2 5
Second approch: Without making any assumptions about the function f ( x ) , we know that x ≤ f ( x ) ≤ x , x ≥ 1 since the assumptions f ( x ) > x and f ( x ) < x can be contradicted: f ( x ) > x ⇒ f ( x ) < x ⇒ x = f ( f ( x ) ) > f ( x ) > x x = f ( f ( x ) ) < x In particular, f ( 1 ) = 1 follows. We can also calculate the derivatives at x = 1 : f ′ ( f ( x ) ) f ′ ( x ) f ′ ′ ( f ( x ) ) ( f ′ ( x ) ) 2 + f ′ ( f ( x ) ) f ′ ′ ( x ) f ′ ′ ′ ( f ( x ) ) f ′ ( x ) ( f ′ ( x ) + 1 ) + ( f ′ ′ ( x ) ) 2 ( 2 f ′ ( x ) + 1 ) = 2 1 x − 2 1 = − 4 1 x − 2 3 = 8 3 x − 2 5 ⇒ f ′ ( 1 ) ⇒ f ′ ′ ( 1 ) ⇒ f ′ ′ ′ ( 1 ) = 2 1 = − 2 ( 1 + 2 ) 1 = 2 ( 2 + 2 ) 2 2 − 1 Therefore, we can use the Taylor expansion f ( x ) ⇒ f ( 2 ) ≈ f ( 1 ) + f ′ ( 1 ) ( x − 1 ) + 2 1 f ′ ′ ( 1 ) ( x − 1 ) 2 + 1 2 1 f ′ ′ ′ ( 1 ) ( x − 1 ) 3 ≈ 1 . 6 3
Moderator note:
Note: The second approach makes the assumption that the function is infinitely differentiable, in order to apply the Taylor Series. As seen in Sharky's solution, this assumption may not hold.
A positive, increasing (even continuous) function might not have a derivative everywhere (E.g. the Cantor function), so the second approach isn't valid.
Note: We can get that the image is R + , hence (with increasing) can conclude that the function is continuous.
Log in to reply
Can the concatenation of two discontinuous monotone functions produce a continuous function?
I agree that my second approach is not a rigorous, mathematical proof. The main problem is that I have not specified the radius of convergence, so the Taylor series may not converge at point x = 2. But I wanted to outline a second approach to suggest that you can come up with the same solution without assuming a power function.
Log in to reply
Can you elaborate on what you mean by "concatenation"? How are you concatenating the 2 functions? If you are referring to "adding" the functions, then adding 2 discontinuous monotone functions will not produce a continuous (monotone) function.
However, if you are referring to my example, note that the cantor function is indeed continuous, and so "cantor + x" is a monotone increasing and continuous function that does not have a derivative on the Cantor set.
The main problem with the second approach isn't the radius of convergence. The main problem is that the Taylor series expansion might not apply because the function is not differentiable. Note: In the proof that Taylor's polynomials converge to the function in a given radius of convergence, we make an assumption that the function is infinitely differentiable.
Log in to reply
@Calvin Lin – I meant the function composition f ( f ( x ) = ( f ∘ f ) ( x ) (I have incorrectly translated German into English). The question is, can a composition of functions, that are not differentiable, produce a function, that is differentiable? The square root function g ( x ) = x is arbitrarily often differentiable. I can not imagine that pathological functions like the Cantor function can produce a well-behaved function like the square root. Although pathological functions can be constructed, they seldom appear naturally. Therefore, I find it natural to assume that the desired function f ( x ) is arbitrarily often differentiable. If you know a counterexample, or even another solution to this problem, I like to be convinced of the opposite.
Log in to reply
@Markus Michelmann – Indeed, my contention is whether the function is differentiable. (We know that the function must be continuous.) As it turns out, it is possible for the composition of 2 non-differentiable functions to be differentiable.
One reason for this misconception is that we want to apply the chain rule: ( f ∘ g ) ′ = ( f ′ ∘ g ) ⋅ g ′ , in order to conclude that g ′ and f ′ exist. However, note that the assumptions of the chain rule is that the functions are differentiable. So, it might be possible for g ′ ( x ) to not exist, but ( f ∘ g ) ′ ( x ) to exist.
As a trivial example, let f ( x ) = 0 when x is rational and 1 otherwise. This function is nowhere differentiable. However, f ( f ( x ) ) = 0 always, so it is (infinitely) differentiable.
As an example of function composition of monotone, continuous, non-differentiable (distinct) functions being differenentiable, let h ( x ) be the cantor function, f ( x ) = h ( x ) + x , let g ( x ) = f − 1 ( x ) (Why does the inverse exist, and is monotone+continous?). Then we have g ( f ( x ) ) = x is differenitable.
Edit: I found a continuous, monotone, not-everywhere differentiable function such that f ( f ( x ) ) = x + 1 , and does not pointwise satisfy f ( x ) = x + 2 1 . So, I'm now much less certain about the validity of the answer to this problem. Let me have a think about it.
why did you assume the power function that you did? is it because we are looking for a function whose exponent is greater than 1/2 but less than 1?
Log in to reply
The sketched function course already suggests that it can be a similar power function as the square root. Otherwise, maybe a certain amount of mathematic intuition can help. This is not a problem you can solve according to the book. Instead, you have to think a little bit, if you don't get the solution right away.
Regarding the second solution, did you mean x ≥ 1 ? The square root of x is greater than x for fractional values of x.
Log in to reply
You are right. I have corrected this typo now. Thanks.
Shouldn't this problem be at least on intermediate difficulty? This seems very easy compared to it being on advanced difficulty.
Log in to reply
While the answer is easily guessed, the proof isn't simple. Note that none of the solutions are rigorous. They all contain an assumption that's not in the question.
First approach: How can we assume that it's a power function? I mean, I should have assumed that and figured out there was an answer, but how do we know there isn't a different formula meeting the same requirements in the problem?
Second approach: Loved the solution, but how are you assuming that the function is differentiable? Is that a dumb question?
Log in to reply
Power functions have a couple of defining features. Mostly that they are 0 when x=0 and 1 when x =1. (This is only in cases where c=1, which means the OP could have assumed this from the beginning)
Those are valid concerns. See my comment at the bottom, along with the threaded discussion.
It's pretty intuitive to guess that f is a power function. It doesn't matter if there are other positive, monotonically increasing functions that satisfy the same identity - for the problem to be valid they would have to all have the same value for f ( 2 ) . Therefore, the solution can be reached by calculating f ( 2 ) for any one of these functions.
Log in to reply
Intuition is very dangerous, and can often be easily misled. As I have pointed out, this problem is invalid as there are multiple values of f ( 2 ) , even with the conditions given.
Log in to reply
@Sharky Kesa – True, but making sure the problem is valid is the responsibility of the setter. In this instance, the setter had made an error. Just now the problem has been changed to be multiple-choice and have a 'cannot be determined' option, so my last comment is no longer valid.
How do you know f is a power function or even differentiable?
If one carefully has a look at the offered picture, the problem is smply solved by the principle of golden ratio, i.e. if a > b > 0 , then a a + b = b a = φ . Here a = x − f ( x ) , b = f ( x ) − x . So, since from a 2 − a b − b 2 = 0 there follows φ 2 − φ − 1 = 0 , its solution is φ = b a = 2 1 + 5 . Here f ( x ) − x x − f ( x ) = 2 1 + 5 , and for x = 2 , we obtain f ( 2 ) = 3 + 5 4 + 2 + 1 0 ≈ 1 . 6 3 7 9 6 . As for the golden ratio, please refer to https://en.wikipedia.org/wiki/Golden_ratio
A function f(f(x)) can also be written as (f o f) (x). A function is a special kind of relation where you have 1 input and it spits out 1 output. That's the definition of a function. Since you take the one function f after the other function f you do the same transformation 2 times in a row.

The question is what is the middle or what is f(x)?
When you start from X and end in Root X you have to change the exponents. So how do you go from exponent 1 to exponent 1/2? Remember you have to do 2 operations or transformations rather to go from X to root X or from 1 to 1/2.
I called the operation p and we have to do this operation 2 times in a row to get from exponent 1 (input) to exponent 1/2 (output):
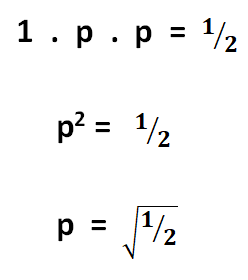
So now we fill in x = 2 and you get the solution 1.63
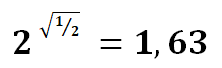
How do you know the function necessarily changes the exponents?
|For this problem, I decided to find the distance between the equation y = x and y = x . We know that all three lines have the same value at x = 1 .
( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2
We plug in the value of x which is 2
( 2 − 2 ) 2 + ( 2 − 2 ) 2
We get the value as 0 . 5 9 once rounded to the second decimal place.
Finally, I added 1 to that value because we know that at x = 1 all the points have the same value.
We end up with the answer 1 . 5 9 , which is an accepted approximation according to the problem.
This is an extremely lucky guess because finish the distance between the two points and adding the arbitrary value of one (we are looking at x=2 so there is no reason to touch 1). Does not geometrically help you at all in this scenario. Without knowing how nesting functions (probably a better name that I have forgotten) works, the best bet would be to to assume that the function that you are trying to approximate near 2 is halfway between the other two functions (it’s not).
So that would mean you find the distance between 2 and the square root of two, divide that by 2 and add the square root of 2. This gives a value of about 1.70 which is probably too far off to be counted as correct.
Log in to reply
This is not a lucky guess, it's Newton's approximation method applied
Log in to reply
Can you elaborate? I do not see how that is relevant.
As Calvin Lin has pointed out, no one has currently gotten a rigorous solution. What I detail here is more of a guideline of a rigorous solution, which explains why there are several possibilities for the function.
Firstly, since the RHS can take any positive real value and this would be defined for any f , we have f surjective. Since f is monotonically increasing, we have f injective. Thus, f bijective, so an inverse exists.
Now, we consider removing the monotonic condition and redefining f as a bijective function in the positive reals satisfying f ( f ( x ) ) = x . Note that by associativity, we have f ( f ( f ( x ) ) ) = f ( x ) = f ( x ) .
We determine that the only fixed point is x = 1 .
Now let g : R + → R + satisfy g ( x ) = x . We consider chains (iterations) of g as A = { … , g − 3 ( x ) , g − 2 ( x ) , g − 1 ( x ) , x , g ( x ) , g 2 ( x ) , g 3 ( x ) , … } and B = { … , g − 3 ( f ( x ) ) , g − 2 ( f ( x ) ) , g − 1 ( f ( x ) ) , f ( x ) , g ( f ( x ) ) , g 2 ( f ( x ) ) , g 3 ( f ( x ) ) , … } , where we choose x such that all elements are distinct i.e. x not a fixed point so x = 1 .
We notice that what f does is create a relation from an element in A to an element in B and vice versa by the associative relation we found earlier. However, this pairing can occur arbitrarily. Thus, without this monotonic condition, we can have a lot of weird functions satisfying.
Now all that's left to show is that if f is indeed monotonic increasing, then the arrows must be arranged such that we have f ( x ) = x 2 1 .
After further working, I have found there are other solutions that don't give f ( 2 ) = 2 2 1 , so this question is flawed. Consider h ( h ( x ) ) = 2 x for h : R + → R + . Any solution to this is equivalent to any solution for f ( f ( x ) ) = x because taking the log of the expression in f gives the expression in h . ( f ( x ) = exp ( h ( lo g ( x ) ) ) )
Thus, we want to find positive, monotonic increasing solutions to h ( h ( x ) ) = 2 x . If we set h ( 1 ) = 2 1 and h ( 2 ) = 1 , and force h to be continuous increasing in the interval [ 1 , 2 ] , we can define h on the rest of R + accordingly, so there exist other solutions.
The above image shows one such example of h I simulated on Geogebra. I fixed the curve between points A ( 1 , 2 1 ) and B ( 2 , 1 ) , and then used the trace-point feature and animated more points that should be on the curve. This function (after iterating it) remains monotonic increasing and satisfies h ( h ( x ) ) = 2 x .
Therefore, this question is flawed.