Halved long division
Below is a long division with some digits hidden. What is the sum of all the missing digits?
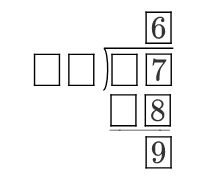
Note that the leading digit of each number cannot be 0.
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
A simpler way to solve this is:
xy * 6 is a 2-digit number, so xy * 6 < 100 ==> xy < 100/6. Can you take it from here?
Log in to reply
Since x y < 6 1 0 0 , x y ≥ 1 0 ⟹ 1 0 ≤ x y < 6 1 0 0 ⟹ 6 0 ≤ 6 x y < 1 0 0 ⟹ 6 0 ≥ ( 1 0 b + 8 ) < 1 0 0 ⟹ 1 0 ≤ 6 1 0 b + 8 < 6 1 0 0 ⟹ 1 0 ≤ 6 1 0 ( b − 1 ) + 1 8 < 1 6 ⟹ 1 0 ≤ 6 1 0 ( b − 1 ) + 3 < 1 6 6 1 0 ( b − 1 ) will be an integer iff b − 1 multiple integral of 6. So b − 1 = 6 n , n ∈ N ⇒ b = 6 n + 1 b = 7 , 1 3 , 1 9 , ⋯ 6 n + 1 Since b is single digit number so only acceptable value of b is 7 . Hence the inequality above becomes 1 0 ≤ 1 3 < 1 6
Is this correct sir @Pi Han Goh ?
Log in to reply
Yes, correct. Well done! :)
Here's a shorter explanation:
The last digit of y * 6 is 8. By trial and error, y = 3 or 8 only.
Since xy * 6 is another 2-digit number, then xy * 6 < 100 ==> xy < 16.6666.
Combining the 2 statements above, we get xy = 13 only. What's left is to complete the long division.
Log in to reply
@Pi Han Goh – Thank you sir !! I could have directly said that last digit product is 8 but I was much interesting to show it is 13*6 = 78 . To do show addition by 10 a step is added . : ) Thank you for your explanation
Log in to reply
@Naren Bhandari – No problem. Glad you've enjoyed it. Do try out my other problems in long division by navigating through the search bar and type "pi han goh long division".
Log in to reply
@Pi Han Goh – I really enjoyed it Sir ! Sure I will be trying that one too. 😊😊
The long division is 0 6 0 1 0 3 \enclose l o n g d i v 0 8 7 0 7 8 9
Let us assign the unfilled boxes as below 0 6 0 x 0 y \enclose l o n g d i v 0 a 7 0 b 8 9 From above long division we can draw out ( 1 0 a + 7 ) − ( 1 0 b + 8 ) = 9 ⇒ a − b = 1 We conclude that the difference of a and b is 1 which makes us clear that they are co-prime( moreover they are consecutive integers) to each other where a > b .
Also we can have 6 × x y = 1 0 b + 8 ⇒ 5 b + 4 = 3 × x y Adding 1 on both sides we get 5 ( b + 1 ) = 3 × x y + 1 or 5 a = 3 × x y + 1 5 a = 3 0 x + 3 y + 1 The range of x is 0 < x ≤ 3 .If we input either x = 2 or x = 3 then a will be two digits number(which is not as a is single digit). So the appropriate value for x is 1 . Entering x = 1 equation becomes 5 a = 3 1 + 3 y This equation will be true and a will be a single digit if 3 1 + 3 y < 5 0 for which the value for y = 3 . Then a = 5 3 1 + 3 × 3 = 8 c c c c c c , b = 8 − 1 = 7 Therefore the sum of a + b + x + y = 8 + 7 + 1 + 3 = 1 9 .
2nd Solution written using the hints provided by Sir @Pi Han Goh
Since x y < 6 1 0 0 , x y > 1 0 ⟹ 1 0 < x y < 6 1 0 0 ⟹ 6 0 < 6 x y < 1 0 0 ⟹ 6 0 < ( 1 0 b + 8 ) < 1 0 0 ⟹ 1 0 < 6 1 0 b + 8 < 6 1 0 0 ⟹ 1 0 < 6 1 0 ( b − 1 ) + 1 8 < 1 6 ⟹ 1 0 < 6 1 0 ( b − 1 ) + 3 < 1 6 6 1 0 ( b − 1 ) will be an integer iff b − 1 multiple integral of 6. So b − 1 = 6 n , n ∈ N ⇒ b = 6 n + 1 b = 7 , 1 3 , 1 9 , ⋯ 6 n + 1 Since b is single digit number so only acceptable value of b is 7 . Hence the inequality above becomes 1 0 < 1 3 < 1 6