Halved Triangle
Consider a line that simultaneously bisects the area and the perimeter of a given triangle.
Only two such lines exists for a triangle of side lengths 7 , 8 , 9 .
If θ is the acute angle between the two lines, find tan θ .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How would you solve it, if only two sides of the triangle are given, and you are told that the triangle has only two area-perimeter bisector lines?
Log in to reply
Only two sides are given means there are infinitely many triangles. I don't think it can be solved.
Log in to reply
I'm saying two sides are given AND it is given that the triangle has ONLY TWO equalizers.
Forget it.
My point is, when a triangle has only two equalizers then it satisfies ( s − b ) 2 + ( s − c ) 2 = ( s − a ) 2 where a is the smallest side and s is the semiperimeter.
This way, even if only sides were given, we could find the third side using the above formula.
Log in to reply
@Digvijay Singh – In that case I think it is equivalent to 3 sides given then it should be able to be solved.
Log in to reply
@Chew-Seong Cheong – To find the third side you would first have to prove that ( s − b ) 2 + ( s − c ) 2 = ( s − a ) 2 . How would you go about that?
Log in to reply
@Digvijay Singh – I thought this is given. I don't understand the equalizer part.
Log in to reply
@Chew-Seong Cheong – Equalizer is a line which simultaneously divides the area and the perimeter into two halves.
Then, depending on the triangle, it can have one, two or three equalizers.
When a triangle has two equalizers only, then its sides satisfies the relation ( s − b ) 2 + ( s − c ) 2 = ( s − a ) 2
Log in to reply
@Digvijay Singh – Oh, let me think about it.
I have done some investigation and found that triangle with a = 7 . 5 , b = 8 , and c = 9 gives two equalizers but ( s − b ) 2 + ( s − c ) 2 = ( s − a ) 2 (last column in the spreadsheet).
Triangle with a = 1 7 , b = 1 8 , and c = 2 5 , which satisfies ( s − b ) 2 + ( s − c ) 2 = ( s − a ) 2 does give two equalizers.
My point is ( s − b ) 2 + ( s − c ) 2 = ( s − a ) 2 is not a condition for two equalizers. Maybe it applies to integer side lengths, but I don't intend to find out.
Log in to reply
@Chew-Seong Cheong – It was mentioned in this article
The lines which bisects the area and the perimeter of a triangle are called Triangle Equalizers. Depending on the triangle, it can have 1, 2 or 3 Equalizers.
Click here for a detailed analysis of such lines
Here's what the halved triangle looks like:
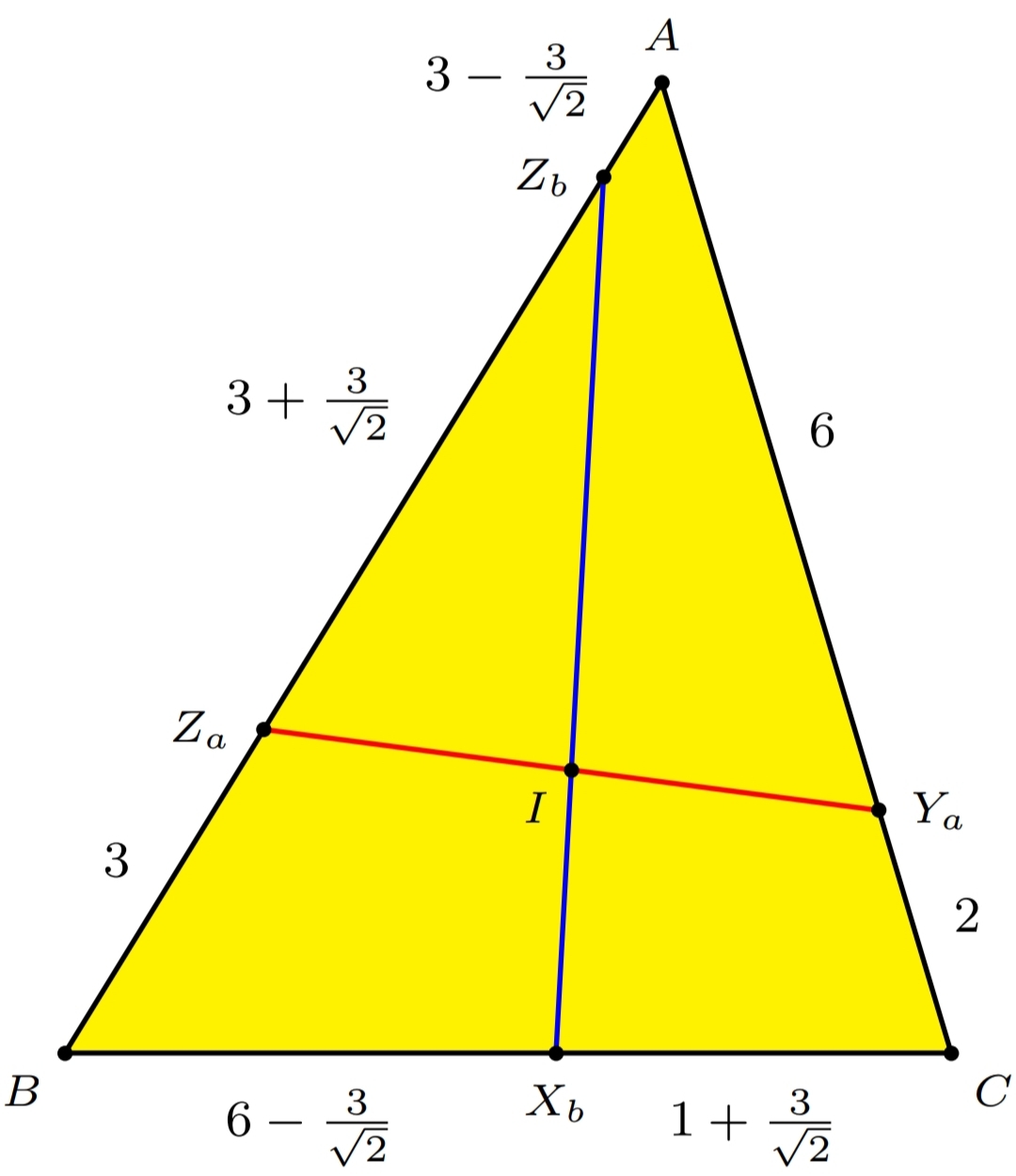

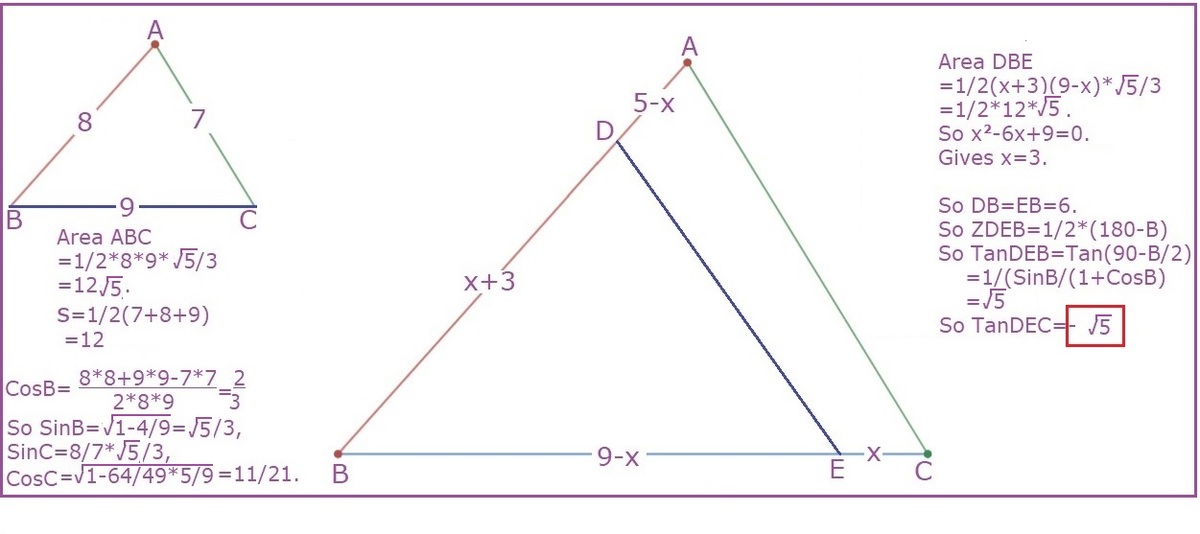
Let △ A B C be the triangle, where C A = b = 7 , A B = c = 8 , and B C = a = 9 . By Heron's formula . the area of △ A B C , A △ = s ( s − a ) ( s − b ) ( s − c ) , where semiperimeter s = 2 1 ( a + b + c ) = 1 2 . Then A △ = 1 2 ⋅ 3 ⋅ 5 ⋅ 4 = 1 2 5 and the perimeter 2 s = 2 4 .
Let E G be one of the lines that simultaneously bisect the area and the perimeter. Then the area of △ B E G , A B = 2 1 A △ = 6 5 and B E + B G = 2 2 4 = 1 2 . If B G = x , then B E = 1 2 − x .
We know that A △ = 2 1 a c sin B and A B = 2 1 x ( 1 2 − x ) sin B . Then we have
2 1 x ( 1 2 − x ) sin B x ( 1 2 − x ) x 2 − 1 2 x + 3 6 ( x − 6 ) 2 ⟹ B G = 4 1 a c sin B = 2 9 ⋅ 8 = 3 6 = 0 = 0 = B E = 6 Rearranging .
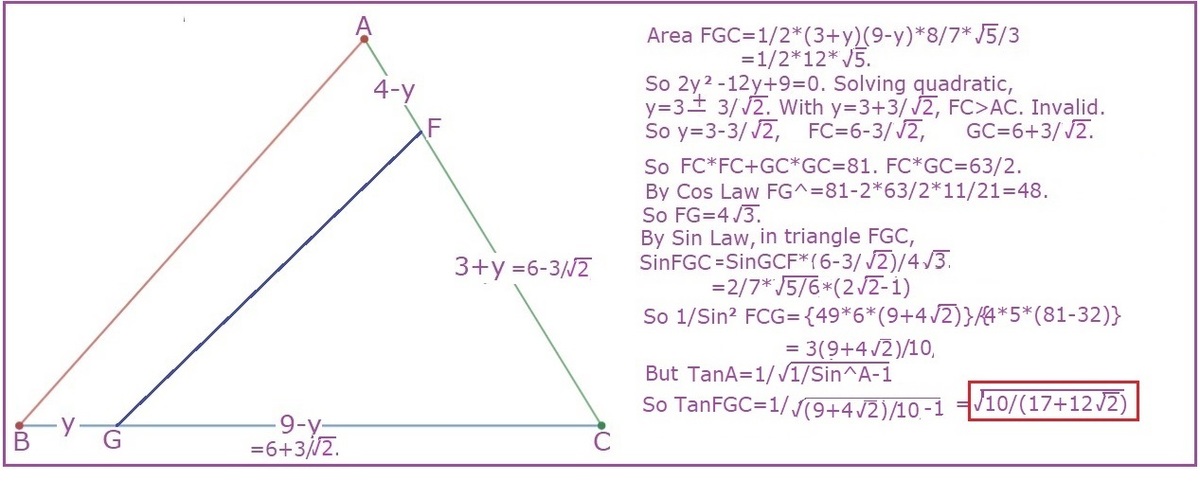
Similarly, let C F = y and C D = 1 2 − y , then:
y 2 − 1 2 y + 3 1 . 5 ⟹ y C D = 0 = 2 1 2 + 1 4 4 − 1 2 6 = 2 1 2 + 3 2 = C F = 2 1 2 − 3 2
For the simultaneous bisecting line opposite ∠ A , we have:
z 2 − 1 2 z + 2 8 ⟹ z = 0 = 6 + 2 2 ≈ 8 . 8 2 8
Since z is longer than the two sides (7 and 8), the line is outside △ A B C . Therefore △ A B C has only two such lines.
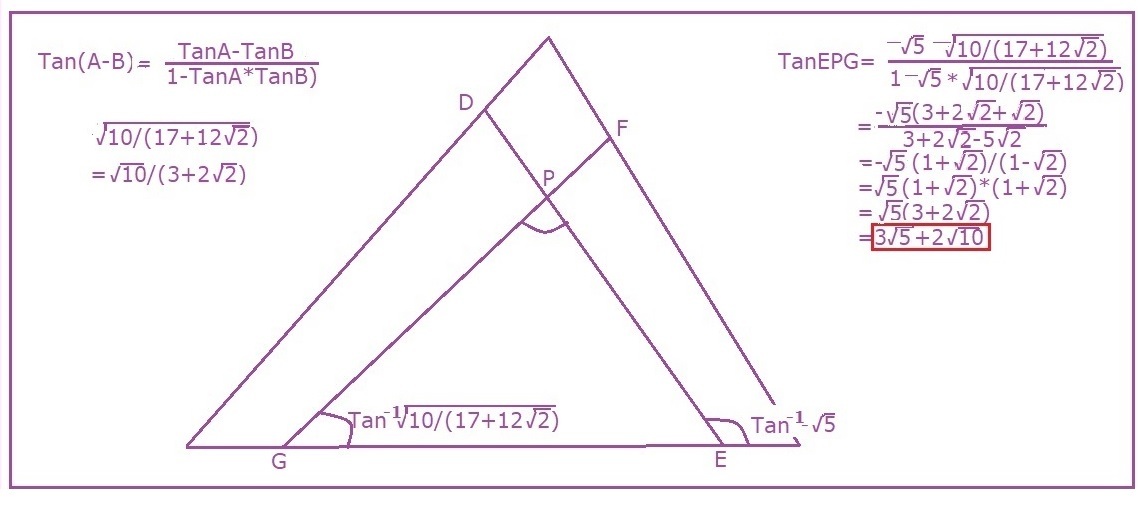
Let ∠ G H F = θ = 1 8 0 ∘ − ∠ E G B − ∠ D F C . Then:
tan θ = tan ( 1 8 0 ∘ − ∠ E G B − ∠ D F C ) = − tan ( ∠ E G B + ∠ D F C ) = tan ∠ E G B tan ∠ D F C − 1 tan ∠ E G B + tan ∠ D F C = 5 ( 3 1 0 − 4 5 ) − 1 5 + 3 1 0 − 4 5 = 5 2 − 7 1 0 − 5 = 3 5 + 2 1 0 See note: tan ∠ E G B = 5 , tan ∠ D F C = 3 1 0 − 4 5
Note:
tan ∠ E G B = B G − B E cos B B E sin B = 6 − 6 ⋅ 3 2 6 ⋅ 3 5 = 5 Since 2 1 ⋅ 8 ⋅ 9 sin B = 1 2 5 ⟹ sin B = 3 5 , cos B = 3 2
tan ∠ D F C = C F − C D cos C C D sin C = 2 1 2 + 3 2 − 2 1 2 − 3 2 ⋅ 2 1 1 1 2 1 2 − 3 2 ⋅ 2 1 8 5 = 3 1 0 − 4 5 Since 2 1 ⋅ 7 ⋅ 9 sin C = 1 2 5 ⟹ sin C = 2 1 8 5 , cos C = 2 1 1 1