Handle the putty wad with care!

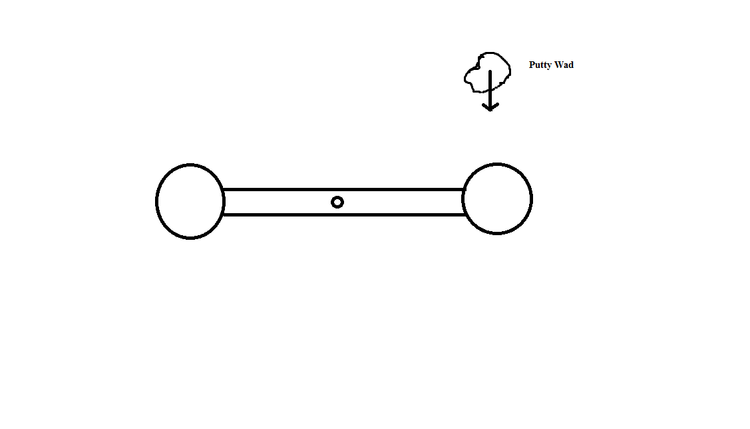The system of putty and balls gets some initial angular velocity $\omega$ , found by conserving angular momentum about pivot.The moment of inertia of the system about pivot is $\dfrac{2M+m}{4} l^2$ , where $M$ is mass of ball, $m$ is that of putty and $l$ is length of rod

$mv \dfrac{d}{2} = \bigg(\dfrac{2m+M}{4} l^2 \omega\bigg)$ .... (i)

Now, right ball and putty will come down and then rise to an angle $\theta$ above horizontal.

Using conservation of energy,

$mg \dfrac{l}{2} \sin \theta = \dfrac{1}{2} \dfrac{2m+M}{4} l^2 \omega^2$ ... (ii)

From (i) and (ii), we get

$\theta \approx \sin \theta = \dfrac{mv^2}{(2M+m)lg}$ in radians

Multiply by $\dfrac{180}{\pi}$ , and put values to get $\theta \approx 1.3^{\circ}$

So, it covers $180 +1.3 = 180.3^{\circ}$

Actually this question has three parts. First ,to calculate the $\omega$ of the system ,second the ratio of the kinetic energy of the system after the collision to that of the putty wad just before.,.

And this has been left for you as a question ! The angular speed comes out to be $0.148 rad/sec$ and the ratio of kinetics energies is $0.0123$ And the third to what angle does the whole system rotates before momentarily coming to a stop.

As the rod rotates, the sum of its kinetic and potential energies is conserved. If one of the balls is lowered a distance $h$ , the other is raised the same distance and the sum of the potential energies of the balls does not change. We need consider only the potential energy of the putty wad. It moves through a $90^{o}$ arc to reach the lowest point on its path gaining kinetic energy and losing gravitational potential energy as it goes. It then swings up through an angle $\theta$ losing kinetic energy and gaining potential energy, until it momentarily comes to rest. Take the lowest point on the path to be the zero of potential energy. It starts a distance $\frac{d}{2}$ above this point, so its initial potential energy is $U_{i}= \frac{mgd}{2}$ .If it swings up to the angular position $\theta$ as measured from its lowest point, then its final height is $\left(\frac{d}{2}\right)(1-\cos\theta )$ above the lowest point and its final potential energy is $u_{f} =mg \times \left(\frac{d}{2}\right)(1-\cos\theta )$ The initial kinetic energy is the sum of that of the balls and wad: $K_{i} = \frac{1}{2}I\omega^{2}=\frac{1}{2}(2M+m)\left(\frac{d}{2}\right)^{2} \omega^{2}$ At it’s final position we’ve $K_{f}=0$ .Conservation of energy provides the relation: $mg\frac{d}{2}+(2M+m)\left(\frac{d}{2}\right)^{2} \omega^{2}= mg \times \left(\frac{d}{2}\right)(1-\cos\theta )$ When this equation is solved for $\cos \theta$ ,the result is $\cos\theta=-\frac{1}{2}\left(\frac{2M+m}{mg}\right)\left(\frac{d}{2}\right) \times \omega^{2}$ On putting the values in S.I. units we get $\cos\theta=-0.0226$ Consequently, the result for $\theta$ is $91.3^{o}$ The total angle through which it has swung is $90^{o}+91.3^{o}=\boxed{181.3^{o}}$ which we can round off to nearest integer.