Hanging Scale
Two masses are tied to a string and hung over a gap, as shown, and you adjust the attachment points of the string until the angles t and u are equal. You then measure that s = 3 0 ∘ and t = 3 6 ∘ .
What is the mass of m ( in k g ) to three decimal places?
Assume that the string is held tight and does not sag.
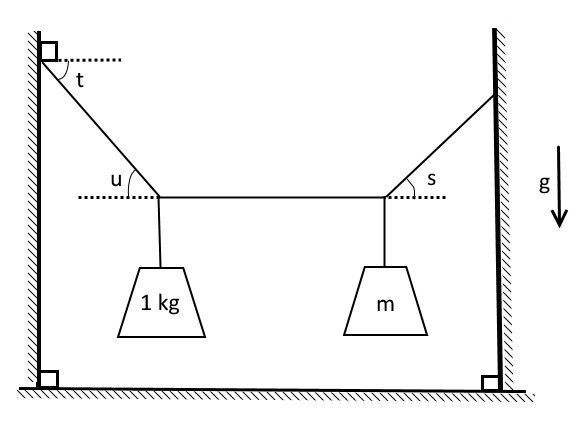
Bonus: If the measurement of the angles has an error of ± 1 ∘ , then how accurate is the mass measurement?
The answer is 0.795.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
So is the tension supposed to be constant throughout all segments of the string? I thought it worked out pretty nicely that there were four stasis equations, and four unknowns, if the tensions were assumed to be different.
Log in to reply
Well, that's true. I had assumed that the points where 3 strands meet were fixed knots. It changes things if the weights are hanging from a loop in which a single strand runs from wall to wall. Let me think about that.
If the two weights are hanging from pulleys rolling on a single strand running from wall to wall, they're going to both end up together, and tension will be uniform along that strand. Equilibrum will exist only if the strand makes equal angles from the vertical where the weights are both hanging together.
If we assume fixed knots, then tension along that strand is not going to be uniform from segment to segment. So, for example, if the tension in the horizontal segment is F , then the tension in the left and right segments would be F S e c ( 3 6 ) and F S e c ( 3 0 )
Log in to reply
Yeah, my result is exactly the same as your "fixed knot" scenario
Log in to reply
@Steven Chase – You probably know that in engineering, they routinely consider all possible forces in every seperate element, so that there would be no surprises. Giant matrices abound. Even matters of how elements come together in a variety of jointed ways, loose or fixed, can significantly matter. I recall one case where by design long threaded rods was supposed to support 2 hotel walkways from the ceiling, but during construction, to save trouble, they substituted shorter rods threaded only at the ends. Instead of using long threaded rods with each walkway supported by a hollow rectangular aluminum box beam on a nut and washer underneath, they used shorter rods terminating just below the upper walkway aluminum box beam, and the same thing from from the top of that beam to just below the lower walkways aluminum box beam. What could go wrong? Both walkways fell down. Maybe I should make this a Brilliant problem.
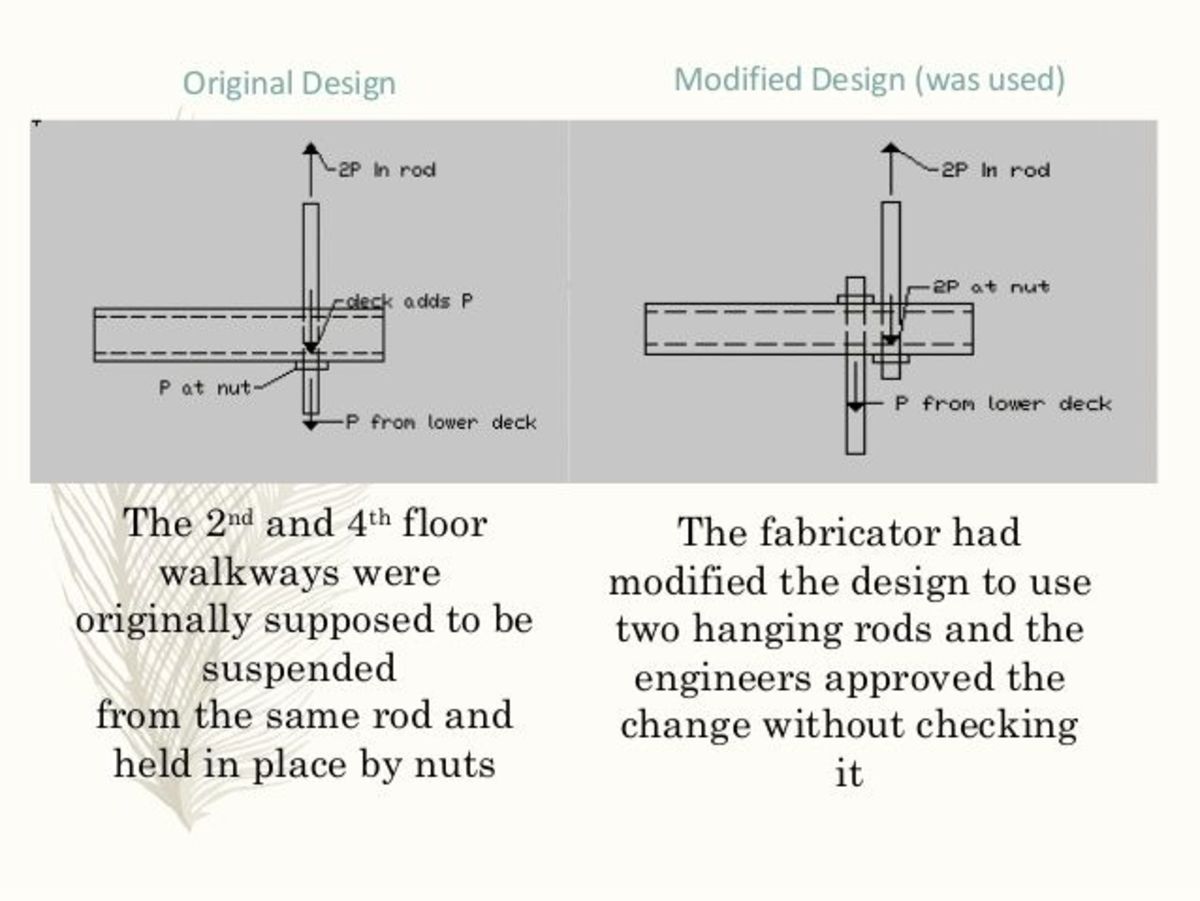
Log in to reply
@Michael Mendrin – That could be interesting. I guess the tricky part would be figuring out which types of reaction forces there should be at each point of interest. The presumably, we could use linear algebra from there?
There are two vertical stasis conditions and two horizontal stasis conditions, for a total of four equations. Linear algebra dictates that there should be four unknowns. Conveniently, there are three string segments. If we treat each segment as having a unique tension, the unknown mass combines with the three unknown tension values to balance with the four equations. Let ( T 1 , T 2 , T 3 ) be the tensions from left to right:
T 1 s i n ( u ) = g T 1 c o s ( u ) − T 2 = 0 T 3 s i n ( s ) − m g = 0 T 3 c o s ( s ) − T 2 = 0
The Mathcad captures below show the solutions assuming perfect angle measurement, and assuming all permutations of 1 degree of angle error. It happens to be the case that the extreme permutations on the variable errors are the candidates for maximum overall error. Therefore, we have one ideal case and four error cases. The ideal case yields ( m = 0 . 7 9 5 ) . The error cases yield ( m = 0 . 8 2 7 ) , ( m = 0 . 7 6 3 ) , ( m = 0 . 7 6 6 ) , and ( m = 0 . 8 2 5 ) , for a maximum possible error of absolute magnitude 0 . 0 3 2 , or about 4 % .
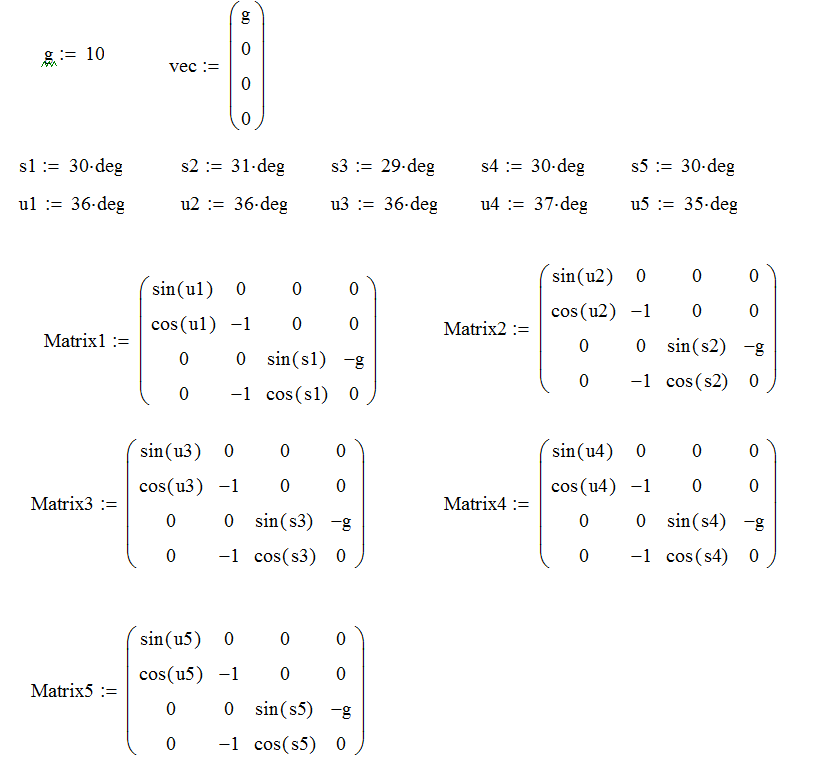

How about use calculus to get error ?
F ⋅ T a n ( t ) F ⋅ T a n ( s ) = 1 m
where F is the horizontal tensile force
The mass measurement has an error of about ± 8 °