Happy Birthday Rajdeep!
∫ − 1 / 3 1 / 3 ( e x + 1 ) ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) d x
If the above integral is equal to b a , where a and b are positive integers with a square-free, find a + b .
This problem is original and was inspired by one of Trevor B's problems. This problem is dedicated to Rajdeep on his birthday.
The answer is 67.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Its pretty amazing how the community comes up with variety of solutions , Great! +1
I have also posted one solution , you might check it :)
Nice solution!! Alternate: Just take out x common from denom .See my solution.
I = ∫ − 1 / 3 1 / 3 ( e x + 1 ) ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) d x Same method as shown by Rishabh above this can be simplified to: ⇒ I = ∫ 0 1 / 3 ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) d x
⇒ I = ∫ 0 1 / 3 ( x 1 + x ) 4 ( x 2 1 − 1 ) d x
Let x + x 1 = t
( 1 − x 2 1 ) d x = d t ⇒ I = ∫ 0 1 / 3 t 4 − 1 d t So ⇒ I = 3 ( x + x 1 ) 3 1 putting limits we can get the answer
Moderator note:
It would be helpful to explain the steps. How does the second line follow from the first? Someone could interpret it as "He forgot to write in the denominator".
Its pretty amazing how the community comes up with variety of solutions , Great! +1
Same method GM!
Same method! +1
First of all, Happy Birthday @Rajdeep Dhingra :)
Now, let I = ∫ 3 − 1 3 1 ( e x + 1 ) ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) d x
Using the property: ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x , we get
I = ∫ 3 − 1 3 1 ( e − x + 1 ) ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) d x = ∫ 3 − 1 3 1 ( e x + 1 ) ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) e x d x
Adding both the values for I , we get:
2 I = ∫ 3 − 1 3 1 ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) d x
Now, substituting x = tan θ and d x = sec 2 θ d θ , we can write 2 I as:
2 I = ∫ 6 − π 6 π ( 1 + tan 2 θ ) 4 tan 2 θ ( 1 − tan 2 θ ) sec 2 θ d θ
Using the identity: 1 + tan 2 θ = sec 2 θ and 1 − tan 2 θ = cos 2 θ cos 2 θ , we get:
2 I = ∫ 6 − π 6 π ( 1 + tan 2 θ ) 3 tan 2 θ cos 2 θ cos 2 θ d θ ⇒ 2 I = ∫ 6 − π 6 π ( sec 2 θ ) 3 cos 2 θ sin 2 θ cos 2 θ cos 2 θ d θ
Further simplifying, we get:
2 I = ∫ 6 − π 6 π cos 2 θ sin 2 θ cos 2 θ cos 2 θ cos 6 θ d θ ⇒ 2 I = ∫ 6 − π 6 π ( sin 2 θ cos 2 θ ) cos 2 θ d θ ⇒ 2 I = 4 1 ∫ 6 − π 6 π sin 2 2 θ cos 2 θ d θ ⇒ 2 I = 4 1 2 1 3 sin 3 2 θ ] 6 − π 6 π ⇒ I = 4 8 1 ( sin 3 3 π − sin 3 3 − π ) ⇒ I = 4 8 2 8 3 3 = 6 4 3
Now, comparing, we get a = 3 , and b = 6 4 . So, the answer, a + b = 6 7 . :)
Moderator note:
Good solution. You can improve it by adding the motivation behind the steps that were chosen. IE We decided to use the integration trick of ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x , because e x + 1 1 + e − x + 1 1 = 1 .
I have also posted one solution , you might check it :)
Same solution! :D
Log in to reply
Lol, yeah. I was surprised too, when he posted the same thing! :D
Log in to reply
I think this would be the most common approach. I did this too. And then there's the other approach by @Gautam Sharma
Log in to reply
@A Former Brilliant Member – Yep! I saw that too!
Its pretty amazing how the community comes up with variety of solutions , Great! +1
We use Weierstrass substitution where x = tan 2 y ⇒ y = 2 arctan ( x ) and then sin x = 1 + x 2 2 x , cos x = 1 + x 2 1 − x 2 , d y = 1 + x 2 2 d x . Now note that ∫ − 1 / 3 1 / 3 ( e x + 1 ) ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) d x can be written as:
8 1 ∫ − 1 / 3 1 / 3 1 + e x 1 × ( 1 + x 2 ) 2 4 x 2 × 1 + x 2 1 − x 2 × 1 + x 2 2 d x
Now in this integral , as x = 1 / 3 , y = π / 3 and x = − 1 / 3 , y = − π / 3 and we change the limits accordingly.Using Weierstrass substitution we transform it to:
8 1 ∫ − π / 3 π / 3 1 + e y sin 2 y cos y d y
Now since 1 + e y sin 2 y cos y is an even function we use the property − a ∫ a e x + 1 E ( x ) d x = ∫ 0 a E ( x ) d x and then we have:
8 1 ∫ 0 π / 3 sin 2 y cos y d y
Now using the substitution u = sin y , d u = cos y d y and required changes in limits , we have:
8 1 ∫ 0 3 / 2 u 2 d u
= 8 1 × 3 u 3 ∣ ∣ ∣ ∣ 0 3 / 2 = 6 4 × 3 3 3 / 2 = 6 4 3
Hence , a = 3 , b = 6 4 , a + b = 3 + 6 4 = 6 7
Its pretty amazing how the community comes up with variety of solutions , Great! + π 2 6 ζ ( 2 )
Its pretty amazing how the community comes up with variety of solutions , Great! +1....:P
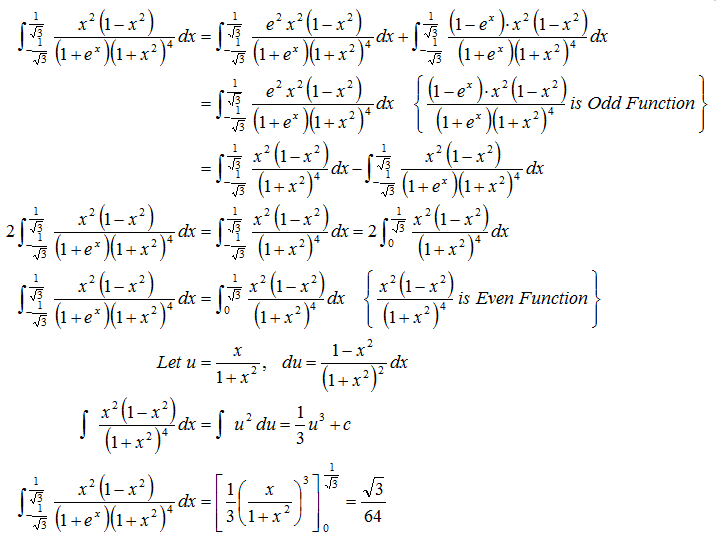
I = ∫ − 1 / 3 1 / 3 ( e x + 1 ) ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) d x I = ∫ − 1 / 3 1 / 3 e x ( ( e x + 1 ) ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) ) d x ( ∵ ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x ) 2 I = ∫ − 1 / 3 1 / 3 ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) d x ⇒ I = ∫ 0 1 / 3 ( 1 + x 2 ) 4 x 2 ( 1 − x 2 ) d x Substitute x = t a n y and use tan y = cos y sin y and sec y = cos y 1 followed by 2 sin y cos y = sin 2 y and cos 2 y − sin 2 y = cos 2 y . I = 4 1 ∫ 0 6 π ( sin 2 2 y ) ( cos 2 y ) d y = 8 1 ( 3 ( sin 2 y ) 3 ) ∣ 0 6 π = 6 4 3 ∴ 3 + 6 4 = 6 7