An algebra problem by An Phạm

Let $f(x) = \dfrac{1}{2} \sqrt[3]{x + 7}.$ Then, the equation is equivalent to $f(f(x)) = x.$ Since $f$ is monotonically increasing, the only way that this can be true is if $f(x) = x$ ; if $f(x) > x,$ then $f(f(x)) > f(x) > x,$ and if $f(x) < x,$ then $f(f(x)) < f(x) < x.$ Therefore, we have

$\begin{aligned} \dfrac{1}{2} \sqrt[3]{x + 7} &= x \\ x + 7 &= 8x^3 \\ 8x^3 - x - 7 &= 0 \\ (x - 1)(8x^2 + 8x + 7) &= 0. \end{aligned}$

The discriminant of the quadratic is $8^2 - 4(8)(7) = -160 < 0,$ so the only real solution to the equation is $x = \boxed{1}.$

Here is a slick way to look at this. Since $x = \frac{1}{2} \sqrt[3]{7+\frac{1}{2}\sqrt[3]{7+x}}$ , we can substitute x for itself in a continued radical style to get:

$x = \frac{1}{2} \sqrt[3]{7+\frac{1}{2}\sqrt[3]{7+ \frac{1}{2} \sqrt[3]{7+\frac{1}{2}\sqrt[3]{7+x}}}}$

This can be chained infinitely:

$x = \frac{1}{2} \sqrt[3]{7+\frac{1}{2}\sqrt[3]{7+ \frac{1}{2} \sqrt[3]{7+\frac{1}{2}\sqrt[3]{7+\cdots}}}}$

We now substitute the entire second iteration onwards for x:

$x = \frac{1}{2} \sqrt[3]{7+x}$

This reduces to basic algebra! Manipulating this into a cubic and factoring out (x-1), we obtain a quadratic with no real solutions.

If we assign $t=\frac{1}{2}\sqrt[3]{x+7}$ , we have:

$\begin{cases} x=\frac{1}{2}\sqrt[3]{t+7}\\ t=\frac{1}{2}\sqrt[3]{x+7} \end{cases}$

$\Leftrightarrow \begin{cases} 2x=\sqrt[3]{t+7}\\ 2t=\sqrt[3]{x+7} \end{cases}$

$\Leftrightarrow \begin{cases} 8x^3=t+7 \\ 8t^3=x+7 \end{cases}$

Assuming that $\underline{x\leq t}\Leftrightarrow x^3\leq t^3\Leftrightarrow 8x^3\leq 8t^3\Leftrightarrow t+7\leq x+7\Leftrightarrow \underline{t\leq x}$

We can see that $x$ is both greater or equal to $t$ and less or equal to $t$ . So $x=t$

$\Rightarrow 8x^3=x+7$

Solving the equation gives us the only real solution, $\fbox{x=1}$ .

Let $f(t) = \frac{1}{2} (t+7)^{1/3}$ and $g(t) = 8t^3 -7$ . Because $g$ is the unique inverse of $f$ , the problem becomes finding a solution $x$ satisfying $f(x) =g(x)$ . However, inverses can only intersect on the line $L(t)=t$ , so we have that $g(x) = x$ . This equation is a cubic with only one root, $x=1$ .

weak proof: Plotting the function shows a straight line even on very large scales, which means y = 0 at only 1 point, (at 1)

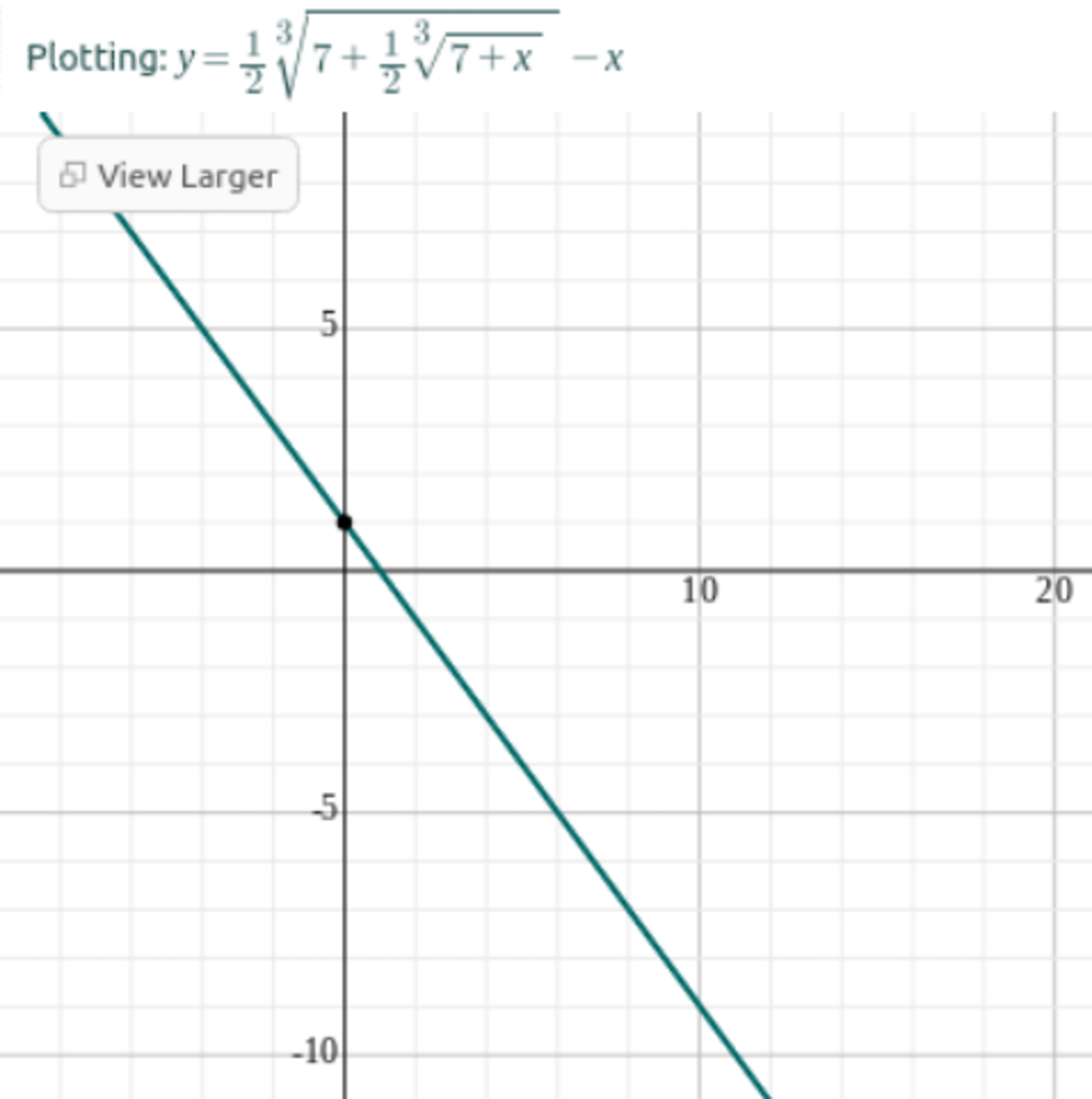
Algebraic manipulation of the equation gives $16x^3-14=\root 3\of{x+7}$ . The functions $y=16x^3-14$ and $y=\root 3\of{x+7}$ are increasing, and so their graphs only intersect at one point, $x=1$ .

I struck lucky with this question!

The question set up invited a solution by a numerical method. I used my calculator to iterate

$0.5 \times \sqrt[3]{7+0.5 \sqrt[3]{ANS+7}}$

By chance I chose ANS = 1 as my starting point, and so the answer popped out with a single iteration!

With other starting values the convergence to the solution is gratifyingly rapid.

One way of answering this question is by using chance. Since there are two possible answers, we have 50% chance to give the correct answer. It worked. Thanks chance !

This is a 9 degree polynomial function so there is 9 solutions to this equation

Roughly draw the diagram of y=8*x^3 and of y=7+(x+3)^(3/2).

And you easily know that the former derivative is greater than the latter one :P

I just thought about the look of the function

(1) $f(x)=8x^3-x-7$

Therefore I calculated the extreme values using the derivative $f‘(x)=24x^2-1$ , which are $x_{1,2}=\pm\sqrt(1/24)$ .

Both values used in equation (1) are negative therefore it exist only one solution (where the equation is zero).