Try not to use L'Hôpital!
Find the value of x → 0 lim ( x 1 − sin x 1 ) .
Alternatively, find the value of the reciprocal function minus the cosecant function, as the variable approaches zero from both sides.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
I went for a short power series approach. Thought it was good to get a variety of solutions on here.
Log in to reply
Don't worry, I did not say that your solution isn't good. In fact, I find your solution brilliant, because of its standardness and its ability to be applied on limits containing a mixture of trigonometric functions and power functions. I also would like to see more solutions. Actually this taylor series does not use l'hopital.
Log in to reply
Thanks Kenny. I enjoyed your question. I am looking forward to seeing more fun questions in the future. Oh, I made sure I didn't use L'Hôpitals. I thought you were contesting the fact that the power series expansions are derived from differentiation. That's what got me a little confused.
Log in to reply
@Isaac Buckley – Well, because taylor series would be "taught" later than the L'hôpital, that's why I made such a note. It's all right actually.
Log in to reply
@Kenny Lau – Actually in England L'Hôpitals isn't even taught until first year undergrad. We do learn Maclaurins series though.
Nice solution! However, taylor series also uses differentiation.
Log in to reply
However? I didn't realise all methods using differentiation are discredited.
Log in to reply
Calm down, calm down. It's just a side note. I apologize.
There are two approaches that I know of. The first approach is using the Squeeze Theorem, and the second approach is using the L'Hôpital Rule.
Squeeze Theorem:
I will only show that x → 0 + lim ( x 1 − sin x 1 ) = 0 . The same method can be applied to show that x → 0 − lim ( x 1 − sin x 1 ) = 0 , while changing the signs.
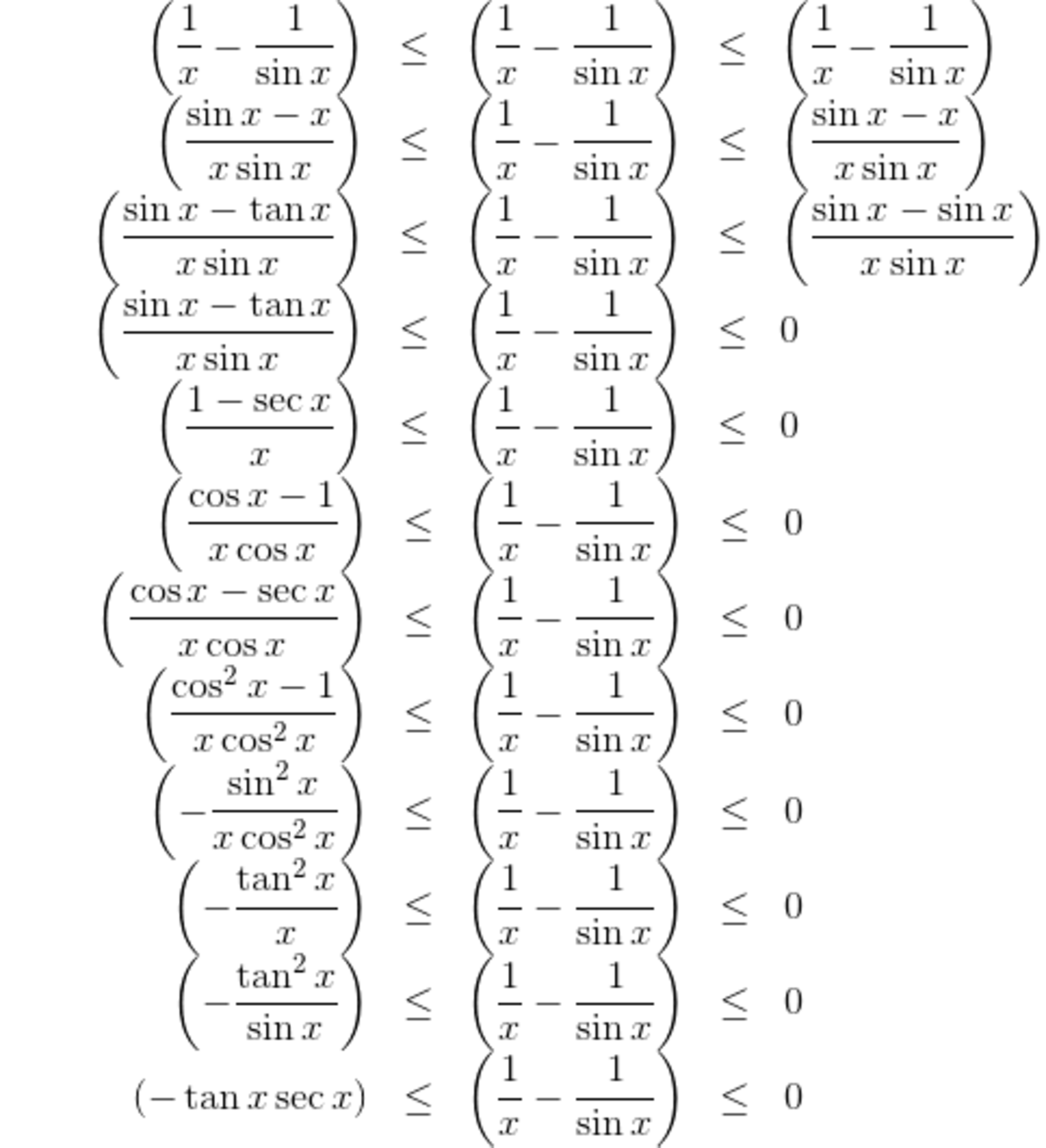
Substitute x = 0 to the left hand side to obtain:
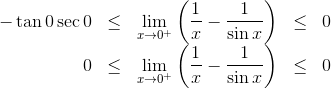
Therefore: x → 0 + lim ( x 1 − sin x 1 ) = 0
L'Hôpital rule:
-
Note that: ( x 1 − sin x 1 ) = x sin x sin x − x
-
Since both the numerator and the denominator of the fraction is zero when x = 0 , this rule can be used.
-
Differentiate both the numerator and the denominator to obtain: sin x + x cos x cos x − 1
-
Since both the numerator and the denominator of the fraction is zero when x = 0 , this rule can be used.
-
Differentiate both the numerator and the denominator to obtain: cos x + cos x − x sin x − sin x
-
The denominator is not zero anymore when x = 0 , so we can substitute x = 0 : cos 0 + cos 0 − 0 sin 0 − sin 0 = 0
Therefore: x → 0 lim ( x 1 − sin x 1 ) = 0
Notes:
-
In the squeeze theorem approach, I used these inequalities that are valid for 0 < x < 1 : sin x < x < tan x cos x < 1 < sec x
-
If instead, 0 > x > − 1 , then: sin x > x > tan x cos x < 1 < sec x
-
Note that the second inequality is unchanged.
All comments/questions/improvements are appreciated.
Here's another approach:
Let L = x → 0 lim ( x 1 − sin x 1 ) and let us assume that the limit exists.
Since the limit exists the left and right hand limits must both exist and equal to L .
∴ L = x → 0 + lim ( x 1 − sin x 1 ) . . . . . . . . . . ( 1 )
and
∴ L = x → 0 − lim ( x 1 − sin x 1 ) . . . . . . . . . . ( 2 )
Replacing x by − x in ( 2 )
L = x → 0 + lim ( − x 1 + sin x 1 ) . . . . . . . . . . ( 3 )
Adding ( 1 ) and ( 3 )
2 L = 0
∴ L = 0
N O T E : In order to use this method we must be sure that the limit exists and is finite.
Lim(x--0)[sin(x) - x]/xSin(x) = Lim[Sinx/xSinx - x/xSin] = Lim[Sinx/x 1/Sinx - 1/Sinx] = [ Lim Sinx/x * Lim (1/Sinx) - Lim (1/Sinx) ] = [ 1 Lim (1/Sinx - 1/Sinx) ] = 1* 0 = 0
Sir, you cannot combine lim sin x 1 − lim sin x 1 to form lim ( sin x 1 − sin x 1 ) .
I simply multiplied the whole term by x and as x tends to zero sinx/x =1 hence 1-1=0
Just for convenience to type, I leave out the lim operator.
[1/x - 1/sin(x)] = [sin(x) - x] / [x * sin(x)]
Using L'Hospital (remember there should be lim operator)
[sin(x) - x] / [x * sin(x)] = [cos(x) - 1] / [sin(x) + x * cos(x)] = [-sin(x) ] / [cos(x) + cos(x) - x * sin(x)]
by substituting x with 0
[-sin(0) / [cos(0) + cos(0) - 0 * sin(0)] = 0 / [1 + 1 - 0] = 0 / 2 = 0
Nice solution! I have edited the title of this question to encourage solving this problem without using L'hôpital Rule.
x 1 − sin ( x ) 1 = x sin ( x ) sin ( x ) − x = x 2 − 3 ! x 4 + o ( x 6 ) x − 3 ! x 3 + o ( x 5 ) − x = x 1 + o ( x ) − 3 ! 1 + o ( x 2 )
∴ x → 0 lim ( x 1 − sin x 1 ) = x → 0 lim ( x 1 + o ( x ) − 3 ! 1 + o ( x 2 ) ) = x → 0 lim x 1 − 3 ! 1 = 0