Harmonic motion timing
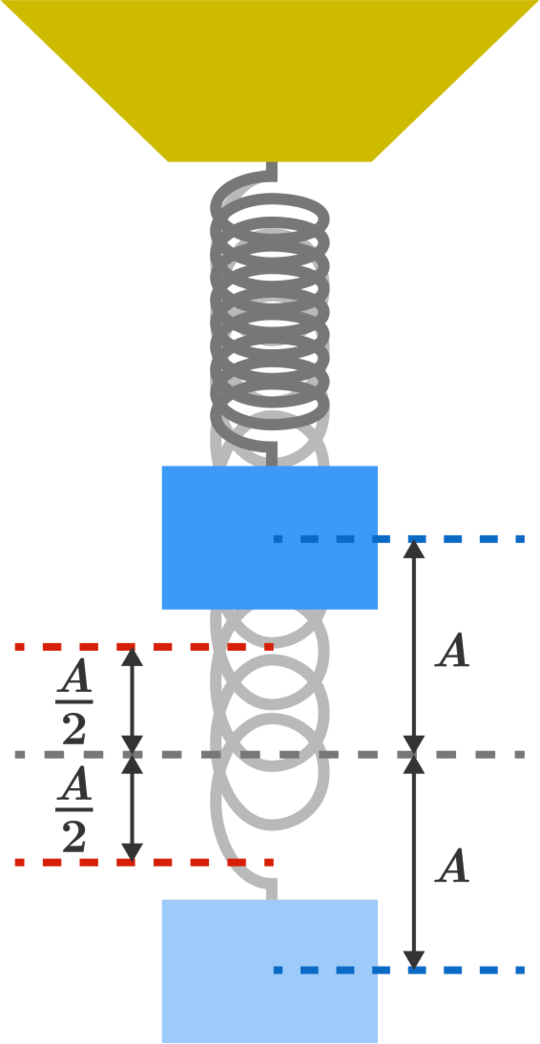
This block oscillates harmonically with amplitude A .
What is the probability of finding the block's center of mass between positions − 2 A and 2 A ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
In one complete oscillation, the block crosses the region -A/2 to A/2 twice making the total time spent in this region = 2T/3. Shouldn't the answer be 2/3.
Log in to reply
30º in one-fourth of the period times 4 is a total angle of 120º in a whole period, which is one-third of 360º, so the answer is 1/3.
The way you have explained this makes complete sense, but the way I looked at it doesn't correlate. I see it as the total amplitude between - A/2 and A/2 being half that of the entire amplitude (A), therefor, the centre of mass (regardless of the direction of movement in this case) spends half of its time traveling through - A/2 and A/2 meaning the answer would be 1/2 right? ("that's quick maths" lol). The only thing I can see that could alter this result would be a momentary pause in momentum at either end of A. Am I missing something? If a car was driving at exactly 30mph along a straight road from point A to D (passing through B and C, 1/4 of total distance each) with another car on the other side of the road ready to drive at 30mph in the opposite direction as soon as the first car arrived at D, would the total time both cars spent travelling through B and C not be 1/2 of the total journey time for both cars? Please school me if I am wrong or point me in the correct direction to learn more as I am 1st year engineering student and this would definitely be useful to know! Thanks in advance 👍🏼
Log in to reply
I think your misunderstanding is of harmonic motion. In simple harmonic motion, like the action of the oscillating block, not only does position vary over time, but so does velocity. In the middle of the block's path, the velocity is a maximum, and at the extremes it is zero where the block turns around. If the block's motion is that of a sine curve over time then its velocity is a cosine curve (d/dx sinx = cosx). So the problem with your car analogy is that the cars are going at constant speeds (linear motion rather than harmonic motion). This is why the block spends different amounts of time in equal lengths of its path.
As Zac Mann said, the speed is not constant in harmonic motion - the block moves fastest through the middle and slows down as it approaches the turning points at the top and bottom.
You can see this in the 1d animation of the spring in Gabriel Chacon's answer. Compare that to the 2d circular motion animation on the right, in which the speed of the green dot IS constant. That's one of the nice things about thinking of harmonic motion as a projection of uniform circular motion.
It made sense now, thanks!
I'm guessing a classic pendulum works the same way. It spends more time on either side than it does in the middle.
Log in to reply
You are right, the motion of a pendulum can be approximated to be similar to the motion of a spring when the amplitude of the pendulum is small.
from where are you getting that it will take 90 degrees to reach A in 1/4 of the period? I am having trouble seeing any of this in the original diagram
Log in to reply
I'm not sure it's possible to deduce from the diagram only. I believe Gabriel is using the fact that that block is oscillating harmonically; so it is undergoing harmonic motion, which can be modeled by a projection of uniform circular motion eg. a sine function. So in short you have to already know about harmonic motion to answer.
and if it spend 1/3 of its time between 0 and A/2 then how is the time it spends between A/2 and -A/2 still 1/3?
Log in to reply
It's within the range for 30 degrees in each quarter of the revolution, so (30 x 4)/(90 x 4) = 1/3.
Log in to reply
wouldn't that be the same as saying the time it spends between 30 degrees and 160 degrees if you are moving in the positive counterclockwise direction? -A/2 corresponds to 160 degrees, correct? just as A/2 corresponds to 30 degrees
Log in to reply
@Matthew Agona – A/2 corresponds to 30 degrees and 150 degrees, and -A/2 corresponds to 210 degrees and 330 degrees. This makes sense because the points half way between the centre and extremes are crossed twice per period (once when the object moves outwards and again as it comes back to the middle. ie in this image, the shaded areas are where it's between -A/2 and A/2 (Image ---> https://imgur.com/a/Y9IgHLq )
It moves faster when it is between 2 A and − 2 A compared to when it between A and 2 A , so it covers more distance in the same time.
Log in to reply
Could you explain this a bit further? I know when the weight is on its way back up its velocity will be increasing and reach a maximum at the instant it passes the 0 point (the equilibrium position) but then it begins slowing down. The interval 0 to A/2 is still between A/2 to -A/2, so how could it be moving faster in one and not the other?
Also, I cannot understand where you got that it would reach A/2 at 30 degrees
Log in to reply
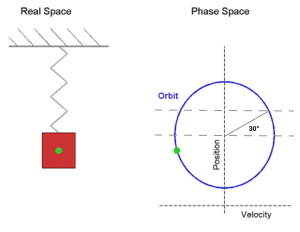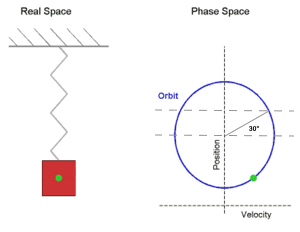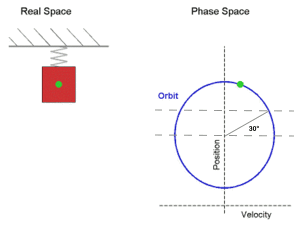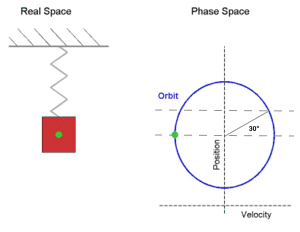
The amplitude (radius of the circle here) is A. At 30 degree, it would reach the amplitude A/2.
He's looking at the right triangle within the circle if you drop a line down from the point on the circle. The hypotenuse will be A (the radius of the circle) and the vertical side will be A/2. So sin(theta) = (A/2)/A = 1/2. So theta is 30 degrees.
The movement of the centre of mass over time produces a cos wave:
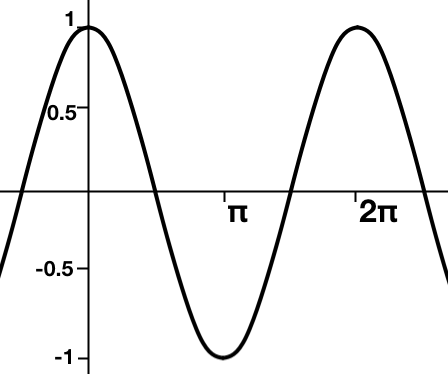(Vertical axis is position, horizontal is time).
To find the probability, we can divide the amount of time the centre of mass is between positions 0 . 5 and − 0 . 5 by the total amount of time. As the wave is uniform, we only need to consider the time between 0 and π to get the full picture.
π a r c c o s ( − 0 . 5 ) − a r c c o s ( 0 . 5 ) = 3 1
shouldn't position A/2 occurs at cos(x)=0.5? So the euqation have arccos(-0.5) and arccos(0.5) instead.
Log in to reply
Sorry, I get my shorthand from C#, so I was using acos instead of arccos.
What will happen if the movement of the centre of mass over time produces a sine wave?
Log in to reply
Sine and cosine only differ by phase, so it won't make a difference. The answer will remain the same. You would be doing π arcsin ( 0 . 5 ) − arcsin ( − 0 . 5 ) = π 6 π − 6 − π = 3 1
It basically does, just starting at a different point in time. I only chose to use Cos because it made the maths slightly easier to visualise.
shouldn't this be arccosine?
Log in to reply
I believe Binky denotes arccos by A c o s .
Sorry, I get my shorthand from C#, so I was using acos. I've edited it to avoid the misunderstanding.
The block will go from mean position to 0.5A in 6 w π time. ( The equation for harmonic motion is y = A s i n ( w t ) )
The block will reach the extreme position, come back to 0.5A, time from there back to mean position = 6 w π .
So, for half the time period, it has spent 3 w π time in the required interval. The same would happen in the other half.
The time period of a simple harmonic wave = w 2 π . Hence, the probability would be w 2 π 2 ⋅ 3 w π = 3 1 .
Isn't it cosine?
Log in to reply
Sine and cosine describe the same motion, just shifted in time by a quarter of the period. ( sin(x) = cos(90 - x) )
Log in to reply
a better explanation is that if the mass is at minimum displacement when t=0, its sine, if the mass is at its maximum displacement when t=0, use cosine, try drawing the graph yourself from the different points.
Yes I know, but, as shown in Binky Mh's solution, this begins from 0, and is more logical
I believe that A cos(wt) represents the velocity. If Asin(wt) is the original position, the 1st derivative is the velocity.
The problem has (should have) an implicit assumption that you are equally likely to find (look for) the block at all times. Then it becomes really simple math. Since the oscillation is harmonic, the angular motion is uniform. The motion is also symmetric about the mean position. That means it is sufficient to consider the region from 0 and +A/2. The block remains within 0 to +A/2 in the phase range [0, PI/6], and again from [5 PI/6, PI] within each half-period. Hence, the required probability = 2 (PI/6) / PI = 1/3.
(1/2)*3=(3/2) n (1/2)/(3/2)=1/3
A simple way of answering the question is realizing that harmonic motion is the projection of uniform circular motion. Starting at angle 0 (equilibrium position), it takes an angle of 30º to reach 2 A and 90º to reach A (in a fourth of the period). Since the angular motion is uniform, the body spends only 3 1 of the time between 0 and 2 A , and this is true also for the remaining three fourths of the period. So the answer is 3 1 .