Hawkeye's problem
Find the area of triangle having lengths of medians as 6 , 8 and 1 0 .
If you get this you will also get this problem .
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Another method :
The area of a triangle = 3 4 times the area of the triangle formed by it's medians
Log in to reply
Didn't Know that! Thanks!!!
i used ur method vaibhav.
Its*. 😉 Good to know that! Thanks!
awesome one nice observation man!
but how do we calculate area formed by medians??
Log in to reply
@Nithin Nithu , We take the lengths of the Medians to be the Sides of a triangle. And then Solve it Using Heron's formula :) :). For Example The triangle formed by the medians Of the given triangle Will have sides 6,8,10(Lengths of median).
Therefore the area of the triangle formed by the medians Is 1/2 8 6 = 24.(Because It is a right angled triangle.)
Therefore the area of the Triangle Is 4/3*24= 32.
I hope you get it now ⌣ ¨
I see it! Thanks!
Haha you didn't even change variables here Take it in good humour.
Log in to reply
Lol , but I read this formula in a book.Just a coincidence... xD
Log in to reply
Haha i searched for more formulaes about area of triangle and landed there and saw they were exactly same.Really funny coincidence.U must be laughing loud i can imagine.
Log in to reply
@Gautam Sharma – May be its a standard notation for median length.
@Gautam Sharma – formulae* xD
Log in to reply
@Nihar Mahajan – Another lol i didn't press 'e ' in formulaes it just got along with s.i wanted to write formulas.
Log in to reply
@Gautam Sharma – Well are you on facebook?
Log in to reply
@Nihar Mahajan – yeah i am on fb
Log in to reply
@Gautam Sharma – did you recieve my friend request? There are many sharmas on fb... even in Indian cricket team ... xD
This image was taken of another problem solved by
@Matt Enlow
. It is a proof without words.
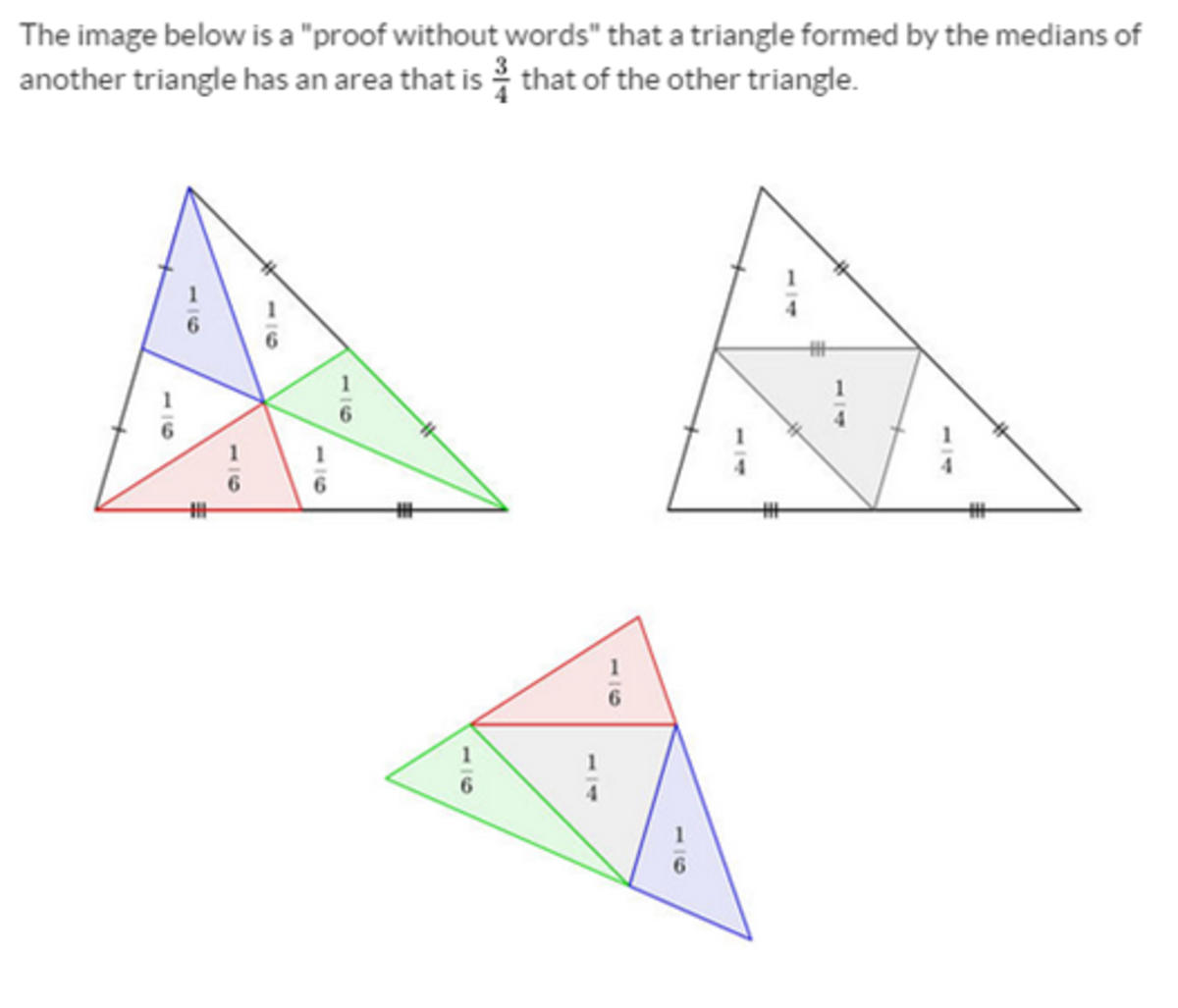
By the lenght of the sides we know that is a rectangle triangle so its area is 2 6 × 8 = 2 4 therefore triangles' area is 3 2 4 × 4 = 3 2
Amazing Proof!
Just use the formula when u have the lengths of all medians .. (4/3) * heron's formula
reference: http://math.stackexchange.com/questions/168701/finding-the-area-of-triangle-if-length-of-medians-are-given
still working from what planet did they get that formula :)
Area of triangle A B C where u , v , w are its medians is given by :
3 1 [ 2 ( u 2 v 2 + v 2 w 2 + u 2 w 2 ) − ( u 4 + v 4 + w 4 ) ]
When u = 6 , v = 8 , w = 1 0 , Area is 3 2 .
Mehul Arora