He was wrong too
You have a (solid) blue cube and an unlimited number of (solid) red cubes, all of which are of the same size. What is the largest number of red cubes that can touch the blue cube along its sides or parts of its sides?
Touching along edges or at corner points does not count.
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
- 9 on top and bottom. Place a cube directly on top, then rotate 45 degrees. This opens up the corners. Two cubes can now be placed on each corner. Repeat for the bottom face. Then two cubes on two opposing vertical faces, and one cube on each of the two remaining faces.
the problem with this solution is that when you put two cubes on two of the corners the edges stick out leaving no room for two on the other two corners.
Can you please explain exactly how to put 9 cubes on the top and bottom side? I don't see how to put more than 7 on top and bottom.
Log in to reply
I agree, see my reply to Ed Speers.
8 is possible, even with some space between those 8 cubes. See also https://math.stackexchange.com/questions/1085687/how-many-unit-squares-can-overlap-a-given-unit-square-without-overlapping-each-o
So you can do this on the top and bottom, and put at least 6 on the sides. Because there are also some gaps between those cubes on the top and bottom, maybe we can also squeeze 2 additional cubes on the sides, although this is not trivial to visualize properly...
Got it bracket Vo
the answer is wrong. The maximum you can get on one end is 7 not 9 then on the remaining sides 2 per side on 2 sides and 1 per side on the remaining 2. thus 7+7+2+2+1+1=20.
Log in to reply
I think you are right! you can only squeeze in 2 red blocks under or on top of two opposite uncovered blue corners but then on the other two sides they stick out so there you would not be able to place again two red blocks, only 1 on each of the two remaining uncovered blue corners, which indeed would give 7 for the top and 7 for the bottom, 2 for the front and 2 for the backside and one for each of the two remaining sides. Hence 7+7+2+2+1+1=20.
8 is possible, even with some space between those 8 cubes. See also https://math.stackexchange.com/questions/1085687/how-many-unit-squares-can-overlap-a-given-unit-square-without-overlapping-each-o
So you can do this on the top and bottom, and put at least 6 on the sides. Because there are also some gaps between those cubes on the top and bottom, maybe we can also squeeze 2 additional cubes on the sides, although this is not trivial to visualize properly...
no way you can place 9 cubes on a single face. maximum is 7, especially if you rotate the center one by 45° as you stated. My solution is 7+7+2+2+1+1=20
Log in to reply
8 is possible, even with some space between those 8 cubes. See also https://math.stackexchange.com/questions/1085687/how-many-unit-squares-can-overlap-a-given-unit-square-without-overlapping-each-o
So you can do this on the top and bottom, and put at least 6 on the sides. Because there are also some gaps between those cubes on the top and bottom, maybe we can also squeeze 2 additional cubes on the sides, although this is not trivial to visualize properly...
I think 24 cube solution should be one with many gaps and tilted cubes
I don't believe 9 on a single face is possible, but 8 is, so the answer could be 8+8+3+3+1+1=24 If you check elsewhere in the comments Samuel Li has replied to Rishy Fishy with a stackexchange link, which demonstrates that 7+7+6+2+1+1 is a possible solution, but potentially even 25 or 26 cannot be ruled out...
As you know guys in geometry a cupe has 6 faces , each face of the blue cube can maximum touch 4 parts of a red cube since all have a unique size . Then if each side of the blue cube touches 4 parts of the red one the blue cube will be touching 24 parts of the blue cube which is the maximum number(4*6=24)
I may be wrong, but I'm pretty sure the answer should be 20 ( 7 on two opposite sides, 2 on two opposite sides, and 1 each on the rest)
Moderator note:
20 is not correct.
You can create a 22 configuration by capping off the top and the bottom with just 1 cube, and then building a "wall" around the 4 faces, where each face intersects 5 squares. We can build to the top and bottom without disregard, and we avoid building to the left, so that the face on the left can build out. See Michael's comment for the configuration.
Rishy Fishy, here's a slightly neater arrangement for the same kind of solution
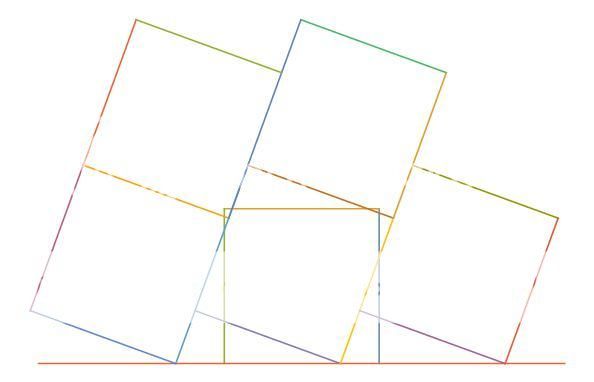
This leads to the 1+5+5+5+5+1=22 solution. Now, everybody seems to be trying to find out how to squeeze in that extra 2 more. I need to be gone for a couple of days now, and maybe on the road to Damascus, I'll get a vision of Jesus telling me how it can be done to get 24.
Log in to reply
Oh, that's much better than mine. I should have checked my rotations more. It's such tiny margins of error that I thought they did not pass through.
Ok maybe I am wrong but what if only touching the edges and corners of the blue cube does not count and touching the sides of the blue cube with the corners and edges of the red cube is a possibility? Than I think 24 is the solution.
I don't have a solution, but I'm sure the answer is 24.
See Guide to the Martin Gardner Papers and
And in this link , search for "24 cubes can face-touch, kiss, a central one of the same size".
Log in to reply
I have the book "Wheels, Life, and other Mathematical Amusements" (which is the one referenced by your links), the 1996 edition. In this book Gardner only gives the suboptimal solution with 20 cubes (7+7+2+2+1+1).
Okay, finally I'm back in town, and I think maybe there does exist a solution after all. A 1+5+6+5+6+1=24 configuration. It's 1:00 am right now and I'm going to sleep. In the morning, I'll see if I can put together a graphic to see if it's a real solution.
Edit: I have 2 critical lines to match in order to avoid an interference. In spite of working on it all morning, I can't seem to close the gap. This is the kind of thing that looks good when you draw a sketch, but computer generated reality shows you something else.
the extra 2 comes from the 2 remaining sides, we put 7 on the face, 7 on the back, then there is 4 more sides around, not just 2
This will not work unfortunately. You have drawn a 2D diagram representative of the optimal 5 cube to side model, however, in 3D space the volumes of the cubes become prohibitive to 4 sides having 5 cubes attached. I truly believe that you'll max out at 20. (7,7,2,2,1,1)
Log in to reply
Take a look at the animation I made below, to see how it all comes together.
Nope. 22 does work. try with your own ice cubes.
My 21 configuration that worked .
Michael Mendrin's 22 configuration .
I still don't know what the solution looks like cause all of my 2 4 's don't work.
Log in to reply
this is awesome. can you follow my thoughts and see what you can get? I think from the way the question is stated, you can have corners and edges of red cubes as long as they touch the sides of the blue cube. so if you put 4 red cubes on a side at the tips of the corners and angle them in so the 4 touch at the center axis of that side (with room to confirm side touching) and the same with variations for the other sides 4x6 I cant confirm because I don't have any cube like things and I don't want to write out the trig.
Log in to reply
Sorry, I don't really understand what you are pinpointing to. But if on each of the 6 faces, all 4 red cubes touch the center point of a side of the blue cube, the cubes will intersect each other.
The face (excluding corners and edges) of a red cube needs to touch the face (excluding corners and edges) of a blue cube.
Otherwise, we can have the standard 26 cube arrangement around a central cube.
Log in to reply
@Calvin Lin – i don't intend to have red edges or corners touch the blue edges or corners, i intend to have red edges and corners touch blue sides. the problem wasn't too clear about that.
Thank you so much for the graphic!
So I did not understand correctly that the blue cube should be completely covered? In the 22 solution there are bits of uncovered blue. If the blue cube needs to be covered the answer is 20.
Log in to reply
There is no requirement for the blue cube to be completely covered from view.
The only requirement is that the red cubes touche the blue cube.
Yea I got 20 as well.
 Solution
Solution
Log in to reply
I had the same answer but wan't able to post a response earlier. Tried various combinations of spin on levels one and three, but always came up with 20.
There is no reason why the cubes would need to be so "grid like". You might get more flexibility form having much looser base, and then having a middle layer that has more vertical variance to it.
Log in to reply
Please provide a visual illustration. I've reached the same answer as Viktor. and I think vertical variance in the middle layer will eat away from the top/bottom layers.
Since no red cube can simultaneously be in face contact with the blue cube in more than one place, any solution can be expressed as how the red cubes are partitioned. For example, the solutions offered here can be expressed as 7+1+2+1+2+7=20, which is not optimum. I know of a 1+5+5+5+5+1=22 solution, which is clear cut. Without actually giving away how the "correct" solution looks like, perhaps how it's partitioned can be revealed, and give others the chance to figure out the final form?
A 8+2+2+2+2+8=24 solution seems incredibly out of reach, and a 7+2+3+2+3+7=24 solution seems far out of reach as well. However, a 7+4+4+4+4+1=24 solution seems possible, while a 4+4+4+4+4+4=24 solution seems even more possible and less restrictive, but I've not been able to find any that works without interference somewhere.
It shouldn't have to be said that any solution cannot exceed 26, which is the kissing number for identical cubes. So a solution of 24 red cubes seems quite remarkable, if only face-to-face contacts are allowed.
Log in to reply
@Michael Mendrin – I do not know what the correct solution looks like.
The best that I have is also the 1+1+5+5+5+5 solution, in which you have to abandon the "grid like" nature of the squares, which is the point that I'm trying to make.
Are you able to get 8 on one face? I'm having difficulty doing so. Can you share a pic if that's possible?
Log in to reply
@Calvin Lin – No, that was a dead end, "8 on one face". After a while, I realized that even if I found such a solution, it wouldn't help get me that 24 overall anyway.
In fact, I think it's possible to have 8 red cubes touch on one face of the blue cube, but so? It won't help anything. If you are interested, I'll get a graphic of how this is done to you, but the solution is very messy and will need some time, and I'm already having to leave town for a couple of days.
Of all the approaches I've tried, only the 4+4+4+4+4+4=24 seems to offer any real hope. But nothing so far, once one gets to the actual calculations for interference.
I also have the same answer with @Viktor Raheem Pacis . Can you @Calvin Lin and @Pi Han Goh prove that the answer is 24?
Could someone explain to me how it is possible to get 24 cubes even if there is no solution found yet.
Solution for 24-cube is found on page 102 It's insane
Log in to reply
WOAHHHHH! @Michael Mendrin @Julian Poon @Viktor Raheem Pacis @Michal Forišek
Log in to reply
I can see how a 7+1+2+1+5+7=23 configuration, a variation of the 7+1+2+1+2+7=20 solution, can work, but I don't see how he squeezes in that extra cube to make it a 7+1+2+1+5+1+7=24 solution. Or is he including the center cube? I'll come back to this later.
The public cannot view the link provided above. The best proven solution, visible to this community so far, is from @Michael Mendrin at 1+5+5+5+5+1=22. Can this purported 24 solution be presented to this forum directly in any way? Until then, most of us are forced to consider it an unexamined assertion or conjecture when it could instead be a proof.
Log in to reply
I've finally got a peek at Martin Gardner's "Wheels, Life, and Other Mathematical Amusements" from which @Alex Li cites the purported 24 cube solution . Having seen it, I must conclude: 1) The passage provides examples of another 22 cube solution as well as a 23 cube solution that has me convinced. 2) These are given as solutions; even those submitted to him were submitted as solutions, and not as proofs. 3) Any reader who wishes to carefully account his conclusions should see that calling this "a 24 cube solution" is an editorial faux pas... The cube faces he counts provide a configuration of 7+7+1+2+1+5, yet across a split line (possibly as copied from its original submitters) he writes it as 7+7+1+1+2+1+5, and we all know that cubes have only six faces. Carefully accounting the touches he tallies prove a miscount: the solution has only ever provided 23 cubes.
How does it work? I'll try to summarize it with our red & blue colors, and note some limitations & inequalities he glosses past. I'll also use compass directions, hoping that aids visualization.
Start with the blue cube resting north against our first red cube. The second red cube will connect to the east face of the first. These two will always pivot on the corner surface of the blue's SE corner. They surface touch on a significant, but almost infinitesimally small, surface of blue. Now let's open "the mouth" between the SW corner of blue and NW of red by a tiny amount, say less than ten degrees, (Note, if it's opened beyond 15 degrees, the model falls apart before we get to the really interesting part.)
Another pair of reds will pivot on the blue's NE corner, and another pair on blue's NW corner. Notice that the first pairs displace the subsequent ones, so our original ten degree opening at blue's SW forces an opening at least twice that at blue's SE, which gets doubled-or-more again at blue's NE. This final angle, let's call it 'e,' is equal to the angle of the last/sixth red cube overhanging the blue cube's west face like a ballcap bill. We want to minimize this angle.
Since the mouth at blue's SW can be reduced to an arbitrarily small but positive amount, the subsequent angles can likewise be downsized to small but positive amounts, even though the final angle will be at least four times the size of the mouth. In the final configuration, the mouth may need to be as small as a single degree, depending on how infinitesimally small our pivot areas touch, and how narrow we need to reduce the ballcap bill's overhang.
Now that we have six red cubes curled around the back three corners of the blue, we're almost done with the top and bottom layers. Raising the blue cube one side unit to the second plane, we drop in a red cube, and rotate it against the first (southern) red cube, toward the east, the back of the mouth's acute angle. It's a tight fit, but whatever tiny area attaches the pair in the NE corner should only be a minor displacement. So long as that tiny area is not excessive, the seventh red's NW corner should match against the West face of the blue.
Layer three should match the angles and orientation of layer one. Now we have the blue cube alone on layer two, touching seven cubes on the layer below and seven more on the layer above. We're nearly there. Into layer two, slide one cube squarely against the north face, another against the south face, and two more straddling the east face.
Finally, we cover the blue's west face with the five cubes as configured in @Michael Mendrin 's 1+5+5+5+5+1 solution... but instead of the edge-limit-line being oriented to our south, it is rotated 180 degrees to come north against the ballcap bill.
This is why it is a difficult solution: There is a positive margin for five cubes to work at a height that is slightly smaller than the cube's height. The ballcap bill's overhang is reduced to an arbitrarily small, yet positive distance. Since that distance is within the margin of the five cubes, they can all touch the blue's west face without overlapping any other cubes. So the final configuration is 7+7+1+2+1+5=23.
*EDITED 2016-08-12: In the fourth paragraph, I've changed "last/seventh" to now read "last/sixth."
Since the link to the solution in one of the comments is now password-protected, the 24-cube solution is explained on the math Stack Exchange: http://puzzling.stackexchange.com/questions/36766/how-many-cubes-can-we-fit-in
I thought I got an orientation for 25 and got all excited. But when I simulated it it was wrong...
Log in to reply
Out of curiosity, what was the partitioning of your attempted solution of 25? Even if it didn't work out? See my comments above about classifying solutions by how the red cubes are partitioned.
Log in to reply
7 + 6 + 4 + 4 + 2 + 2 There was hardly any symmetry in my 2 5 arrangement and so I made an error visualising it.
The answer should be 22. I hope they did not consider edges intersection.. Then it would have 24 cubes, just as a rubik's cube have.
I think I have a solution for a 24 configuration, please correct me if I'm wrong. In the middle of the top face you place one cube but 45° rotated. So you have 4 small triangles near the vertices of that face where you can each place two additional cubes. So that would be 1+4×2=9 cubes for the top face. Do the same with the bottom face. Then the remaining 4 faces can be used for 6 additional cubes. So we have a total of 2×9+6=24 cubes touching the inner cube.
Log in to reply
You can't actually do that, the cubes will overlap. Max on 1 face is 8,
Let me see if someone can explain this to me. I can see the top and bottom being able to be touched by nine cubes each. The center one is a diagonal and you can add two to each side of that center one. (18) Then two sides can only be touched by two each. You can't angle these so there is no way to add more than two. So we now have 22 touching the blue cube. Two side remain. There is no room for more than one on each side. (2) This equals 24.
In order to get more cubes touching the blue cube the top and bottom each need to have more than nine and there is no way to do it.
Challenge Master is wrong. It is only possible to get seven on two sides then the wall allows on 1 or 2 tiles.
Help @Chase McCloskey
i got 24
9 at the top and bottom total 18 then 2 at two sides this makes total 22 and at last 1 on remaining two sides
Log in to reply
How can 9 be at the top? Mind if you provide a visual representation of your solution?
As you guys know "In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex."
So now we can take one square face ,like this...
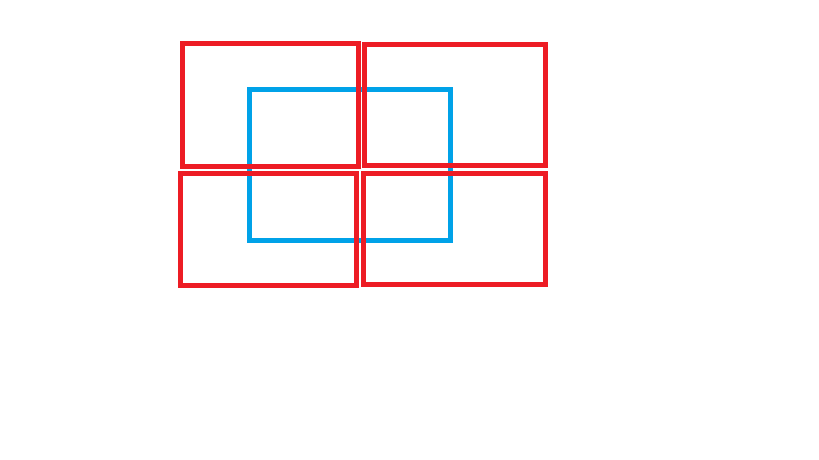 In above image you can see if you want to cover full surface of a blue square shape with red square shapes with maximum number of red squares ...The count will be 4 in this case.
So now we know already that a cube has 6 faces like this so by visualizing this in 3-Dimensions we can say the total number will be 24(4*6)!!
In above image you can see if you want to cover full surface of a blue square shape with red square shapes with maximum number of red squares ...The count will be 4 in this case.
So now we know already that a cube has 6 faces like this so by visualizing this in 3-Dimensions we can say the total number will be 24(4*6)!!
Note: I have visualized this already but I don't know how to help you guys in that .So my advise is first just think about 2-D shape and then go for 3-D...! Feel free to correct me !!
The cubes would intersect each other, since on each face, the cubes extend outwards over the edge of the block, on all 4 sides. The thing that makes this problem so hard is that visualising in 2D and then simply generalising it in 3D by having copies of the 2D design would not work since the interactions of the cubes on each face has to be considered.
By your argument, it is possible to create a configuration of 7 × 6 = 4 2 . See Viktor Raheem Pacis's comment on that.
Log in to reply
Thanks for your recommendation about Viktor Raheem Pacis's comment, but as I see it won't help in this problem. Apparently we can't any generalization in case of these type of problems, here the only thing which can help is visualizing things only! Happy to hear more from you!
I thougt it the same way as Samand. We put 4 cubs on two opposite sides. Then 2 on the adjacent sides, and finally only 1 on each of the two others. I got 14, but seems wrong..
If we have 4 on 2 sides. We can only have 2 on the adjacent sides and will be left with space for 1 only on the sides left over. I thought 14 is the answer.
The answer should be 14. 4 on 2 opposite sides (8) 2 on 2 different opposite sides (12) and 1 on each remains side (14). You can't have 4 cubes touching each side because it would create barriers making it impossible to have 4 cubes touching on all 6 sides!
2 faces each 4 as in picture = 8, then 2 opposing faces each 2 = 4 then last 2 opposing faces with 1 each = 2 Totalling 14
Ok... this does not not work the way it is explained... you can place 4 cubes touching 1 side.. that is true but notice they exceed the bounds of the cube... which means that the red cubes facing the perpendicular would collide with the other cubes... so you could only stack 4 on 2 of the blue faces.. also the way this question is phrased is bad.. saying that corners do not count is bad because where a corner begins and ends is subjective
14 should be correct as if you tried to put four red cubes on each side of the blue cube, the red cubes would interfere with each other preventing them from touching the blue cube. You could place 4 on top and bottom sides (visualize like on a die, sides 1 & 6), 2 on the front and back sides ( die faces 2 & 5), but only 1 each on the left and right sides ( die faces 3 & 4 )
The answer should be 14 . . . . first put 4 red cubes (try it with dice) in a square on the table then put the blue cube in the center. now you will find out it is not possible to put 4 red cubes on the side, you can only put 2 red cubes on 2 sides touching the blue cube and 1 on the 2 other sides (once the space is occupied you can not use it). Now take 4 red cubes in a square and put them on top of the blue cube. Now you used 14 cubes (dices) . If anybody can get 24 red cubes to touch the blue cube (by the rules above) send me a video of it.
i think the max no of red square which can cover blue square is 7 not 4.. since 7 is greater than 4
Log in to reply
Here I didn't intend the literal meaning for the maximum number of red square, I used it for just visualizing things. Try to make some adjustment in mind for the each facets at the same time then you will get the answer. I hope I had helped in this ! Happy to help anytime, so can ask again if you don't get this!
The maximum amount of cubes you can have on any given face is 4, there are 6 faces of a cube so you times 4 by 6 to reach the answer of 24.
Your solution is wrong, because the cubes will intersect with each other.
6 faces and each faces by 4 red cubes. check by drawing a square and divide into 2 square and rectangle or 4 squares and these can only fit the cubes. you fit 4 cubes touching it's face