Hedral

You've got a tetrahedron and four different colors, say- Red, Green, Blue and Yellow. Each face has to be painted with a different color.
How many total number of distinct possibilities of painting the tetrahedron are there ?
Details : The tetrahedron has four equilateral triangular faces and six equal edges.
Hint : Do consider the symmetry.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
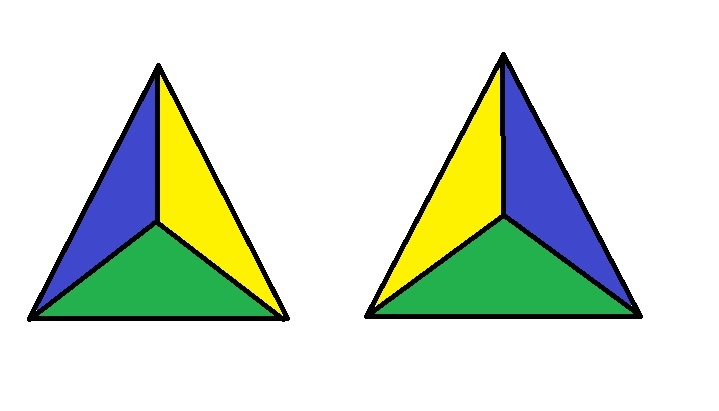
Considering the symmetry, we can always keep one face with a particular color downwards.
Now we assume that the colors are A , B , C a n d D
I take color A at the bottom(you can take any color of your choice, it won't affect the result). So, I get a similar looking geometry (looking from the top) :
Now there are three empty faces (which we can assume as three empty places in a circle to be filled) and three colors to be filled. So total number of ways to fill them = 2 ! = 2
One would say that he will take all the other faces at the bottom, calculate the number of ways and sum them up. This is not going to work. You can try taking different colors at bottom. The two results by taking any color at bottom would be identical respectively.
These are the two cases that would be generated if we take red at the bottom.