Hemisphere E-Field (Quantitative)
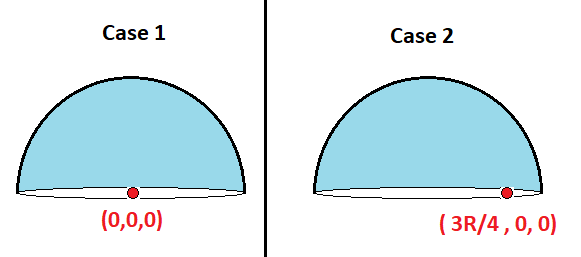
A hollow hemispherical shell of radius R with uniform area charge density has the center of its base at the origin in the x y z coordinate system. Its base is parallel to the x y plane.
In Case 1, there is a test point at ( x , y , z ) = ( 0 , 0 , 0 ) . In Case 2, there is a test point at ( x , y , z ) = ( 4 3 R , 0 , 0 ) .
Let E 1 be the magnitude of the electric field at the test point in Case 1. Let E 2 be the magnitude of the electric field at the test point in Case 2.
Consider the following ratio:
α = E 1 E 2
What is the value of α ?
The answer is 1.342.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Greetings. Thanks for the solution. Is there a singularity at u = 1?
Log in to reply
I would imagine not, although I would expect there to be a discontinuity in E at that point. I would expect the electrostatic potential to be continuous.
@Steven Chase , Can you please tell me a good physics book where i can practice (learn techniques) more questions of this kind? It would be very helpful.
Log in to reply
What aspect do you want to know more about? There is nothing special about the physics here. It's just field superposition from a bunch of tiny elements. Regarding the math, you can either do it analytically (as per Mark's solution), or numerically with a computer.
Log in to reply
@Steven Chase – @Steven Chase , I want to learn more about elemental physics. Questions in which i have to take elements and integrate it.
Log in to reply
@Priyanshu Mishra – One of the first things I did along those lines was to derive all the moments of inertia listed in my high school physics textbook
Log in to reply
@Steven Chase – Can you suggest one of them? Is springer engineering mechanics 3 good one?
Log in to reply
@Priyanshu Mishra – It's been awhile since I've been in school, but I'd say just about any textbook is probably fine. I think you'll learn even more from thinking of your own exercises (or by doing problems on this website).
Log in to reply
@Steven Chase – @Steven Chase , ok
can you please tell any website where i can draw physics diagrams and use them in posting questions at brillliant?
@Mark Hennings , I am not familiar with the three expression written in brackets in integration process. What does that mean?
Can't i do this problem without polar coordinates?
Log in to reply
I am integrating vectors, and inside the brackets are the relevant vector components.
Note that ∫ 0 π ( 1 6 2 5 − 2 3 cos θ ) 2 3 sin θ ( cos θ − 4 3 ) d θ = 1 6 ∫ 0 π ( 2 5 − 2 4 cos θ ) 2 3 sin θ ( 4 cos θ − 3 ) d θ = 1 6 ∫ − 1 1 ( 2 5 − 2 4 x ) 2 3 4 x − 3 d x = 3 8 ∫ − 1 1 [ ( 2 5 − 2 4 x ) 2 3 7 − ( 2 5 − 2 4 x ) 2 1 1 ] d x = 9 2 [ 2 5 − 2 4 x 7 + 2 5 − 2 4 x ] − 1 1 = 0 With a suitable system of polar coordinates, we have E 1 = ∫ 0 π d θ ∫ 0 π d ϕ 4 π ε 0 σ R 2 sin θ R 2 1 ⎝ ⎛ sin θ cos ϕ sin θ sin ϕ cos θ ⎠ ⎞ = 4 π ε 0 σ ∫ 0 π ⎝ ⎛ 0 2 sin θ π cos θ ⎠ ⎞ sin θ d θ = 4 π ε 0 σ ⎣ ⎡ ⎝ ⎛ 0 θ − 2 1 sin 2 θ 2 1 π sin 2 θ ⎠ ⎞ ⎦ ⎤ 0 π = 4 ε 0 σ j On the other hand E 2 = ∫ 0 π d θ ∫ 0 π d ϕ 4 π ε 0 σ R 2 sin θ R 2 ( 1 6 2 5 − 2 3 cos θ ) 2 3 1 ⎝ ⎛ sin θ cos ϕ sin θ sin ϕ cos θ − 4 3 ⎠ ⎞ = 4 π ε 0 σ ∫ 0 π ( 1 6 2 5 − 2 3 cos θ ) 2 3 sin θ ⎝ ⎛ 0 2 sin θ 2 π ( cos θ − 4 3 ) ⎠ ⎞ d θ = 4 π ε 0 σ ∫ 0 π ( 1 6 2 5 − 2 3 cos θ ) 2 3 2 sin 2 θ d θ j = π 1 2 8 ∫ 0 π ( 2 5 − 2 4 cos θ ) 2 3 sin 2 θ d θ E 1 so that α = π 1 2 8 ∫ 0 π ( 2 5 − 2 4 cos θ ) 2 3 sin 2 θ d θ This integral can be evaluated in terms of elliptic functions, obtaining α = 9 π 8 ( 2 5 K ( − 4 8 ) − E ( − 4 8 ) ) = 1 . 3 4 1 1 9 It is worth noting that a generalisation of these arguments shows that the electric field is E ( u ) = 2 π ε 0 σ { u 2 ( 1 + u ) 1 + u 2 K ( ( 1 + u ) 2 4 u ) − u 1 + u E ( ( 1 + u ) 2 4 u ) } j at a point on the x y -plane a distance u R from the origin. The singularity in this expression at u = 0 is removable.