Hemisphere Mechanics |20-09-2020|
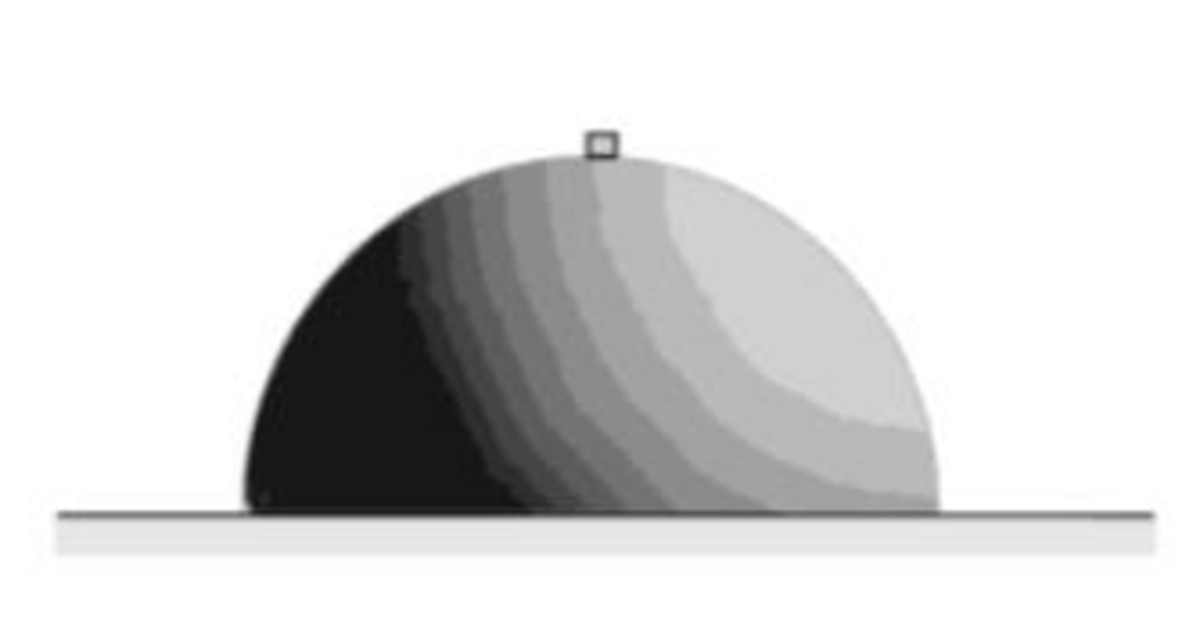 A hemispherical bowl is placed on a frictionless horizontal floor and a small disc is placed on the top of the bowl as shown in the figure. The disc and the bowl are of equal mass and there is no friction between them. The disc is slightly pushed horizontally so that it starts sliding down the bowl with a negligible speed. At what angular displacement of the disc measured from a vertical line through the centre of the bowl will the disc lose contact with the bowl?
A hemispherical bowl is placed on a frictionless horizontal floor and a small disc is placed on the top of the bowl as shown in the figure. The disc and the bowl are of equal mass and there is no friction between them. The disc is slightly pushed horizontally so that it starts sliding down the bowl with a negligible speed. At what angular displacement of the disc measured from a vertical line through the centre of the bowl will the disc lose contact with the bowl?
Answer comes in the form of
c
o
s
−
1
α
Type
α
=
?
||row 1 col 1||row 1 col 2||
||row 2 col 1||row 2 col 2||
The answer is 0.732.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This can be solved analytically by solving the above set of linear equations for θ ¨ , then using the conservation of momentum along X and conservation of energy to solve for θ ˙ and finally using th0se expressions to solve for θ after equating N to zero. Please try yourself and share your attempt.
@Karan Chatrath Thank you so much for solution.
@Karan Chatrath Yes I will share my attempt within 2-3 hour.
@Karan Chatrath By the way , why they have taken small disc? Can't they say a small particle.
Log in to reply
It does not matter, because the question specifies that the small disk slides on the hemisphere. If it said '(purely)rolled down' the hemisphere, then it would have mattered.
Log in to reply
@Karan Chatrath
Exactly, as I expected.
By the way in the topic Rotation i have little bit confusion regarding rolling problems .
Are you comfortable with rolling question?, so I will post that type question.
Log in to reply
@Talulah Riley – I may not be able to solve a very difficult one, but I will try if you post.
@Karan Chatrath I think this is a more comprehensive solution. Thanks; I did it a little more like Lil Doug, actually.
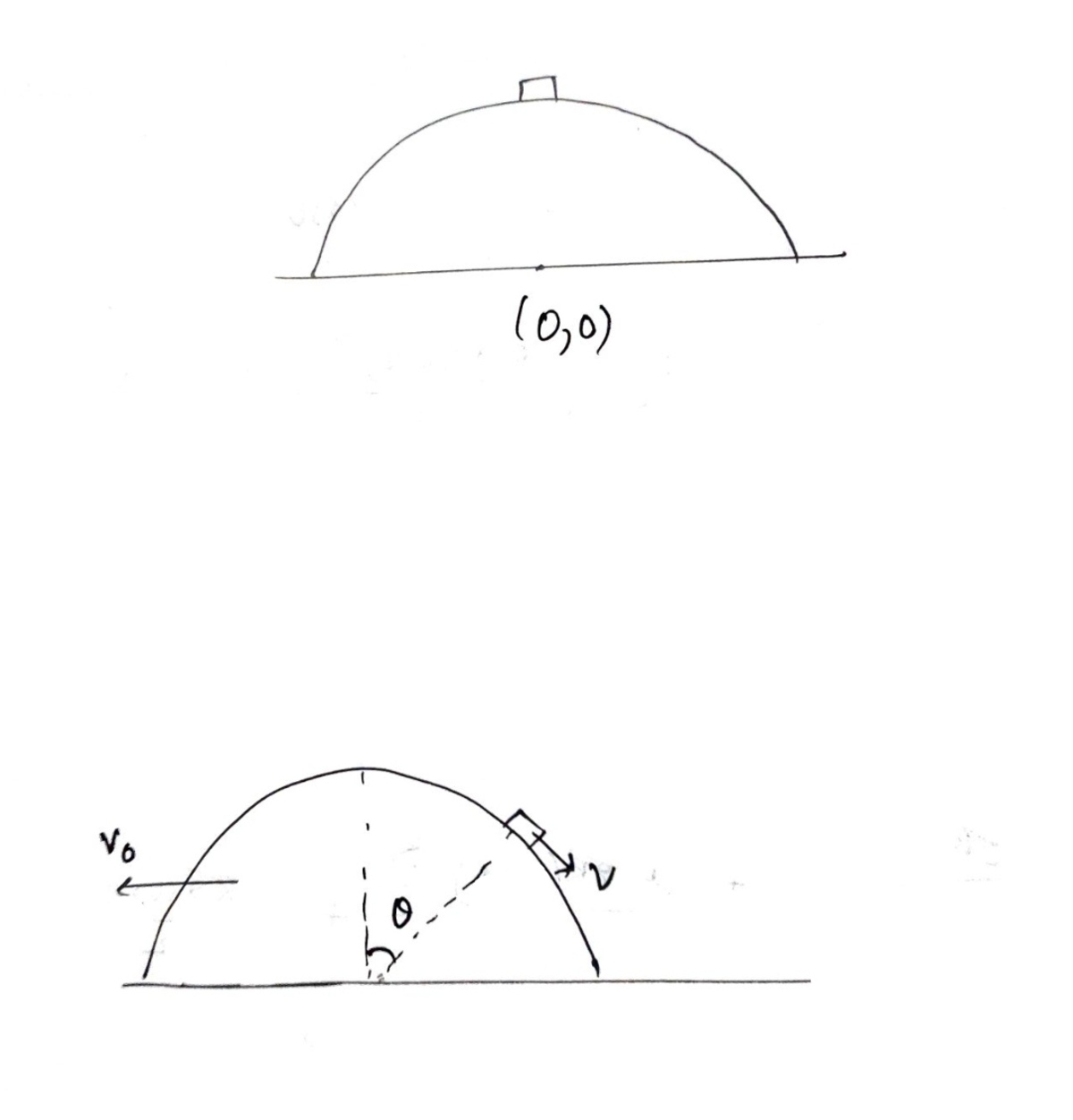
The velocity of that small disc
v
is with respect to hemisphere frame .
And the velocity of that
v
0
of that hemisphere is in ground frame.
So,
F
x
=
0
So let's conserve momentum in
x
direction
0
=
−
m
v
0
+
m
(
v
cos
θ
−
v
0
)
After this conserving energy as always
m
g
R
=
2
1
m
v
0
2
+
2
1
m
(
v
0
2
+
v
2
+
2
v
v
0
cos
(
π
−
θ
)
)
+
m
g
(
R
−
R
cos
θ
)
And the last equation normal to the inclined plane when it losses contact normal reaction will be zero
N
=
0
Which gives the equation
R
m
v
2
=
m
g
cos
θ
After solving these 3 equations patiently gives
cos
θ
=
3
−
1
,
2
,
−
1
−
3
The only reasonable value of
cos
θ
seems to be
c
o
s
θ
=
3
−
1
i got 2/3. how isn't it 2/3?
Numerical solution this time. Let the coordinates of the hemisphere and disc be respectively:
x h = s y h = 0 x d = s + R sin θ y d = R cos θ
Let the reaction force radially outward acting on the disk be N . Drawing a free body diagram and applying Newton's second law gives:
m x ¨ h = − N sin θ m x ¨ d = N sin θ m y ¨ d = N cos θ − m g
Crunching out derivatives, plugging them above and re-writing the equations in a matrix form gives:
⎣ ⎡ m m 0 0 m R cos θ − m R sin θ sin θ − sin θ − cos θ ⎦ ⎤ ⎣ ⎡ s ¨ θ ¨ N ⎦ ⎤ = ⎣ ⎡ 0 m R θ ˙ 2 sin θ m R θ ˙ 2 cos θ − m g ⎦ ⎤
⟹ ⎣ ⎡ s ¨ θ ¨ N ⎦ ⎤ = ⎣ ⎡ m m 0 0 m R cos θ − m R sin θ sin θ − sin θ − cos θ ⎦ ⎤ − 1 ⎣ ⎡ 0 m R θ ˙ 2 sin θ m R θ ˙ 2 cos θ − m g ⎦ ⎤
s ( 0 ) = s ˙ ( 0 ) = θ ( 0 ) = 0 θ ˙ ( 0 ) = 1 0 − 4
Taking m = R = 1 and g = 1 0 the following simulation code is prepared: