Heronian Triangle Dissection B
A Heronian triangle of sides ( 1 9 5 , 2 1 0 , 2 2 5 ) is dissected by a blue line.
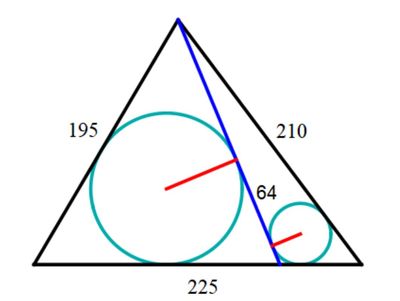
A circle is inscribed in each of the smaller triangles.
The distance between the two tangent points on the blue line is 6 4 .
What's the length of the blue line?
Note: Many thanks to those that have reported a mistake with this problem, which has been fixed.
The answer is 182.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Let the 2 2 5 side be split into lengths of x and 2 2 5 − x , and let the length of the blue line be s . Then the distance from the top vertex to the meeting point of the blue line with the left incircle is 2 1 ( 1 9 5 + s − x ) , while the distance from the top vertex to the meeting point of the blue line with the right incircle is 2 1 ( 2 1 0 + s − ( 2 2 5 − x ) ) = 2 1 ( s + x − 1 5 ) , so that 6 4 = 2 1 ( s + x − 1 5 ) − 2 1 ( 1 9 5 + s − x ) = x − 1 0 5 and hence x = 1 6 9 . The Cosine Rule gives the left-hand angle as having cosine 6 5 3 3 , and hence s = 1 8 2 .
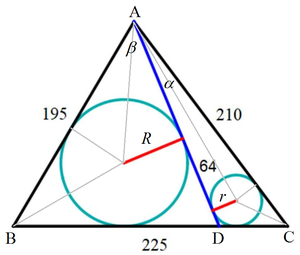
Label the figure as shown. Let ∠ D A C = α and ∠ B A D = β , the radius of the big and small circles be R and r respectively. We note that:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ tan 2 α r − tan 2 β R = 6 4 tan 2 α r + tan 2 C r = 2 1 0 tan 2 β R + tan 2 B R = 1 9 5 ⟹ r = tan 2 α + tan 2 C 2 1 0 tan 2 α tan 2 C ⟹ R = tan 2 β + tan 2 B 1 9 5 tan 2 β tan 2 B . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
Then ( 1 ) becomes tan 2 α + tan 2 C 2 1 0 tan 2 C − tan 2 β + tan 2 B 1 9 5 tan 2 B = 6 4 . . . ( 1 a ) .
Using cosine rule : 1 9 5 2 = 2 1 0 2 + 2 2 5 2 − 2 × 2 1 0 × 2 2 5 cos C , we get cos C = 5 3 . Using half-angle tangent substitution , 1 + tan 2 2 C 1 − tan 2 2 C = 5 3 ⟹ tan 2 C = 2 1 . Similarly, we get tan 2 B = 7 4 and tan 2 A = 3 2 . Since 2 α + 2 β = 2 A , ⟹ tan 2 β = 1 + 3 2 tan 2 α 3 2 − tan 2 α = 3 + 2 tan 2 α 2 − 3 tan 2 α . Let t = tan 2 α ; then equation ( 1 a ) becomes:
2 t + 1 2 1 0 − 2 − t 6 0 ( 3 + 2 t ) 5 6 t 2 + 4 4 1 − 5 6 ( 8 t − 1 ) ( 7 t + 5 6 ) ⟹ tan 2 α = 6 4 = 0 = 0 = 8 1 Rearrange As t = tan 2 α > 0
By sine rule , the length of the blue line A D is given by:
sin C A D ⟹ A D = sin ( 1 8 0 ∘ − α − C ) 2 1 0 = sin ( α + C ) 2 1 0 sin C = 6 5 1 6 × 5 3 + 6 5 6 3 × 5 4 2 1 0 × 5 4 = 1 8 2 Note that sin ( 1 8 0 ∘ − θ ) = sin θ and sin α = 1 + t 2 2 t = 6 5 1 6
A beautiful solution of this problem was given by Chris Lewis . The only change is in the distance between the two tangent points. Following him, we get the final equation connecting the length of the blue line l as 2 2 5 l 2 = 2 2 5 ( 1 9 5 2 + 1 6 9 2 ) − 1 6 9 ( 1 9 5 2 + 2 2 5 2 − 2 1 0 2 ) = 7 4 5 2 9 0 0 , or l = 2 2 5 7 4 5 2 9 0 0 = 1 8 2 .
I hope Chris Lewis will post his solution again. I'm sorry I had to take it down the first time around. I feel bad about that.
Log in to reply
Thanks both - now posted!
Log in to reply
Finally you were able to draw the diagramme. How to draw these?
Log in to reply
@A Former Brilliant Member – I just copied the original diagram into MS Paint and added the labels. @Michael Mendrin , what software did you use for the original?
Log in to reply
@Chris Lewis – Mathematica, which does have some downsides.
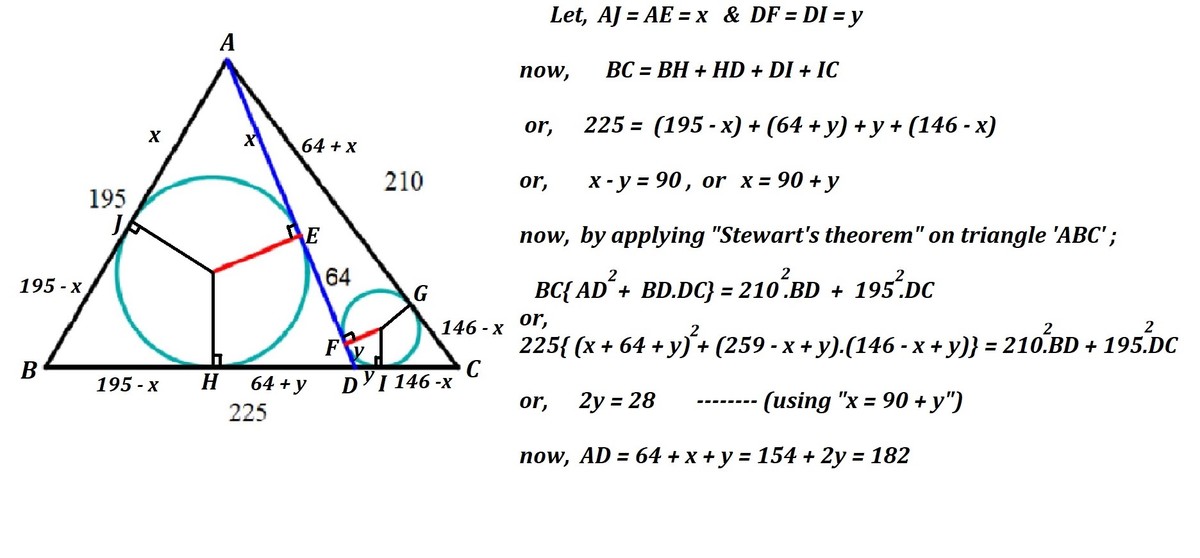
Per the diagram below, let the triangle be A B C , with A B = 1 9 5 , B C = 2 2 5 , C A = 2 1 0 , and let the point the blue line meets B C be D .
Further, let the tangency point of the incircle of Δ A B D on B D be E and the tangency point of the incircle of Δ A C D on C D be F .
Now, the distances to the tangency points along A D are equal to D E and D F (using this property) - that is, D E − D F = 6 4 .
We have D E = 2 1 ( A D + B D − A B ) and D F = 2 1 ( A D + C D − C A ) .
Subtracting, we get D E − D F = 2 1 ( B D − C D + C A − A B ) .
Substituting in, this is 6 4 = 2 1 ( B D − C D + 2 1 0 − 1 9 5 ) , so that B D − C D = 1 1 3 .
Also, B D + C D = B C = 2 2 5 ; so B D = 1 6 9 and C D = 5 6 .
Using the cosine rule in triangles Δ A B C and Δ A B D , we find
cos B = 2 A B ⋅ B C A B 2 + B C 2 − C A 2 = 2 A B ⋅ B D A B 2 + B D 2 − A D 2
Solving, we find A D = 1 8 2 . A nice bonus fact is that both Δ A B D and Δ A C D are also Heronian.