Straightedge and compass - Hexagon
How many moves does it take to construct 6 points in the shape of a regular hexagon?
For example, to get 3 points in the shape of an equilateral triangle you only need two moves:
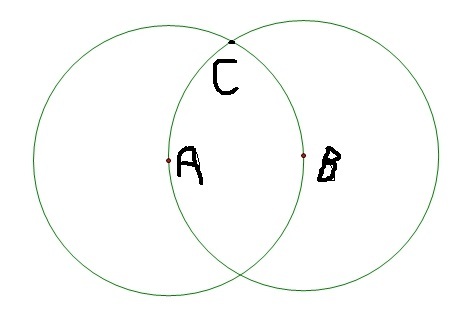
That's two circles drawn.
All terminology in this question is explained in the first note of my straightedge and compass set. More straightedge and compass constructions can be found there.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I took into account that we had to start from scratch. Please, change this, Wen! @Wen Z
Log in to reply
Starting from scratch, it does take 4 moves. I don't see the issue.
Log in to reply
I see my problem! I thought it was collapsible compasses, not incollapsible!
Log in to reply
@Sharky Kesa – As my solution shows, it doesn't matter even if the compass is collapsible.
Thanks for defending . For better presentation, I have modified.
Sorry. I saw it now only. Thank you. I have now given all steps plus a diagram.
I cannot prove that it cannot be constructed with less than 4 moves, but I can prove that 4 moves are enough.
- Construct a circle ω 0 centered at O .
- Pick a point on ω 0 , call it A . Construct a circle ω 1 centered at A with radius A O .
- Construct the line A O . It intersects ω 0 on A and a new point, D .
- Construct a circle ω 2 centered at D with radius D O .
Let the intersections of ω 0 and ω 1 be B and F . Let the intersections of ω 0 and ω 2 be C and E so B and C are on the same side of A D . The hexagon is A B C D E F .
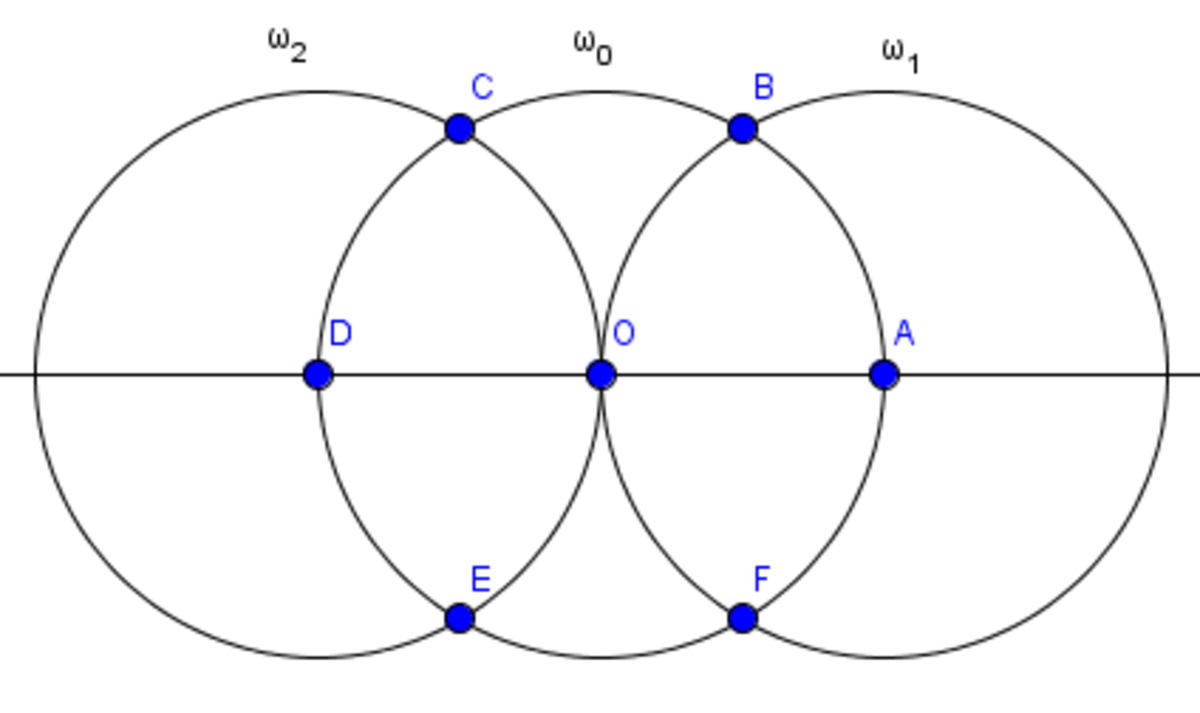
Actually, we can do this in 4 steps with compass alone, no need for straightedge at all. I'll follow Ivan Koswara's diagram:
Step 1 and 2 same as Ivan's.
Step 3. Use B as center, BF as radius draw an arc, it'll intersect circle O at D
Step 4. Use A as center, BF as radius draw an arc, it'll intersect circle O at C and E
Now we are done!
(2) From a point A on the circumference of this circles, draw another circle radius r.
................Name the top point of intersection as C and the bottom as G.
(3) From B draw a line through A to intersect the left circle at E.
(4) With center E, radius r, draw a circle to intersect the left circle at D on top, F at bottom.
BCDEFG is the Hexagon. r=length of the side of the Hexagon.