Hexagon and a circle
Does there exist a hexagon whose 6 vertices lie on a circle, and whose internal angles are 7 0 ∘ , 9 0 ∘ , 1 1 0 ∘ , 1 3 0 ∘ , 1 5 0 ∘ , 1 7 0 ∘ in some order?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
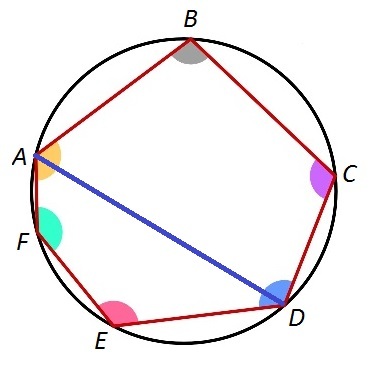Assume that such polygon exists. Without loss of generality, let us draw
A
D
. We see that we have two cyclic quadrilaterals:
A
B
C
D
and
A
D
E
F
. Now, for cyclic quadrilaterals, the sum of the measures of opposite angles are supplementary. Thus
∠
B
A
D
+
∠
C
∠
F
A
D
+
∠
E
=
1
8
0
∘
=
1
8
0
∘
Since
∠
A
=
∠
B
A
D
+
∠
F
A
D
, then adding the two equations gives
∠
A
+
∠
C
+
∠
E
=
3
6
0
∘
Here,
3
6
0
≡
0
(
m
o
d
2
0
)
. Now, each of the angles
{
7
0
∘
,
9
0
∘
,
1
1
0
∘
,
1
3
0
∘
,
1
5
0
∘
,
1
7
0
∘
}
is
≡
1
0
(
m
o
d
2
0
)
, so that the sum of any three of them is
1
0
+
1
0
+
1
0
=
3
0
≡
1
0
(
m
o
d
2
0
)
, a contradiction. Thus, such polygon
is not possible
.
Moderator note:
Note that while the given angles sum to 720 degrees, and it is indeed a necessary condition to have a cyclic hexagon, this answer demonstrates it is not sufficient .
Another necessary condition, as the answer explains, is that alternating angles sum to 360 degrees.
In addition, another necessary condition is that each angle of a cyclic polygon is less than 180 degrees. This is satisfied in the problem.
It is clear that this condition (A+C+E = 360) is necessary. Is this condition also sufficient for a cyclic hexagon?
Log in to reply
In fact, another requirement is that none of the angles is greater than 180 (do you see why?). I suspect this is sufficient. Let me list out my initial working.
Claim: If α 1 ≤ α 3 ≤ α 5 < 1 8 0 ∘ , α 2 ≤ α 4 ≤ α 6 < 1 8 0 ∘ with α 1 + α 3 + α 5 , α 2 + α 4 + α 6 = 3 6 0 ∘ , then there exists a cyclic hexagon with α i as the internal angles.
Proof: We will construct such a cyclic hexagon with vertices V i , where the angle at center is ∠ V i O V i − 1 = θ i > 0 . In order for ∠ V i − 1 V i V i + 1 = α i . we require that ∠ V i − 1 V i V i + 1 = ∠ V i − 1 V i O + ∠ O V i V i + 1 = 1 8 0 ∘ − 2 θ i + θ i + 1 .
This gives us the equations θ i + θ i + 1 = 2 ( 1 8 0 − α i ) . Now, let's set 2 ( 1 8 0 ∘ − α i ) = β i . The given conditions are equivalent to β 1 ≥ β 3 ≥ β 5 > 0 , β 2 ≥ β 4 ≥ β 6 > 0 , β 1 + β 3 + β 5 = β 2 + β 4 + β 6 = 3 6 0 ∘ .
(This is where I get stuck with showing that there are positive solutions to the equations. We have essentially 5 linearly independent equations (removing θ 6 + θ 1 = β 6 , because that is guaranteed by β 1 + β 3 + β 5 = β 2 + β 4 + β 6 .)
There is nothing that states that the diagram is to scale. If the sum of internal angles of a polygon is 180(n - 2) then the sum of the interior angles of a hexagon is 720 degrees. All angles are colored (although one is gray which is a color). 70 + 90 + 110 + 130 + 150 + 170 = 720 The sum of the angles COULD be 720.
If this is not the intention of this problem, then the question is poorly constructed.
Log in to reply
You are missing the point of the question. Yes, a necessary condition is that "sum of internal angles of a hexagon is 720". However, that conditions is not sufficient .
This solution points out that another necessary condition is "sum of alternate internal angles of a hexagon is 360". This condition is not satisfied in the problem.
Note: I am asking if this condition is sufficient for a cyclic hexagon.
How do you know angle C and angle E are exactly 90 degrees. Can you explain more, thank you.
Log in to reply
The answer doesn't state that. It just uses supplementary angles, and then combines the equations to note that three of the angles must add to 360 degrees. Since there is no trio of values in the possible angles where this is true, the polygon is not possible.
What is actual solution of this question please provide me
Log in to reply
This solution is complete. What is your concern?
{This is not complete solution}
The solution of this problem is based on the following rule:
In any cyclic n -gon with even n , the sum of one set of alternate angles (the first, third, fifth, etc.) equals the sum of the other set of alternate angles.
It's then easy to conclude that polygon with such angles cannot exist. But, let's derive above statement for cyclic hexagon:
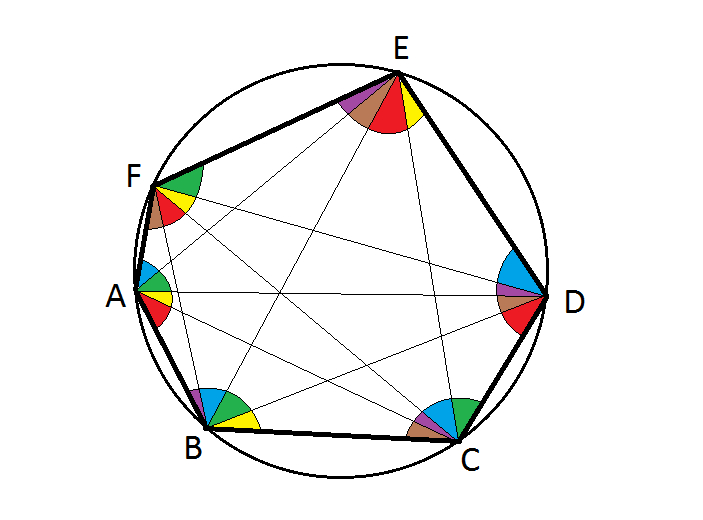
Applying the rule which states that angles subtended by chord on same segment are equal, we come to the following expression:
4 ( R e d + Y e l l o w + G r e e n + B l u e + P u r p l e + B r o w n ) = 7 2 0 ∘
or
2 ( R e d + Y e l l o w + G r e e n + B l u e + P u r p l e + B r o w n ) = 3 6 0 ∘
Notice that three alternate angles added up have 2 angles of every color. Hence, their sum is 3 6 0 ∘ .
By similar method or by induction, above-mentioned rule can be proven for any other even n .
Great generalization!
An easier way to show this is to relate the angle to the "measure" of the arc. (Fill in the details) If the circle has radius 1, how is angle ABC related to the major arc AFEDC? In this way, the alternating angles correspond to angles ABC, CDE, EFA, and hence are related to the major arcs AFEDC, CBAFE, EDCBA, and we've gone around the circle exactly twice!
No. Since one of the angle is 90°, the two adjacent angles have to be on the diameter and the acute angle 70° can neither be in the same semi-circle which contains 90° nor in the semicircle opposite to it. So the 70° angle is adjacent to 90° and is on the diameter. Since the chord joining angles 1 of 90° and the other angle adjacent to 70° is subtending angle 70° on one side, the angle subtended on circle on the other side will be 110°. But there are three angles on the other side of chord subtending 70°, so each will be more than 110° , leaving the angle 110° to be the angle adjacent to 70°. Having determined the position of angles 90, 70 and 110, let us call them angles 1, 2 and 3 in the anticlockwise direction. Continuing to move anticlockwise, the chord joining angles 2 and 4, subtending angle 110 at angle 3, will subtend angle 70° at angle 1, leaving the balance of 90-70=20° to be subtended by chord joining angles 4 and 6 and thereby necessitating the angle 5 to be
180 - 20=160°. But there is no angle of 160°, hence the proposed hexagon is not possible.
The internal angles of a polygon add up to 180 times the number of triangles in the polygon: a triangle is 180, Square=360, pentagon=540 and hexagon=720. The angles given sum to less than 720 so such a hexagon is not possible.
Moderator note:
To clarify, this solution is incorrect.
The given angles do sum up to 720 degrees, indicating that it's possible to form a hexagon. However, we do not yet know if we can form a cyclic hexagon .
That's why I got it wrong. They do add up to 720.
Log in to reply
A necessary condition is that "sum of internal angles of a hexagon is 720". It is true that the given angles sum up to 7 2 0 ∘ . However, that condition is not sufficient for us to obtain a cyclic hexagon . (We can form a hexagon with such angles, but such a hexagon might not be cyclic)
This top solution points out that another necessary condition is "sum of alternate internal angles of a hexagon is 360". This condition is not satisfied in the problem.
They sum to 720, and I failed the answer
Me too - shall look at the 'why it isn't' solutions when I'm feeling less busy
I got it wrong too because I simply added up the angles and as they equalled 720 assumed it ticked the box of possibly being an irregular hexagon. I didn't think about whether all the apexes lay on a circle.
However, after reading all of these solutions you are all missing the point. Re-reading the question:
"Six points on a circle form a hexagon, AS SHOWN IN THE DIAGRAM. Is it possible that the measures of the colored angles are..."
No it obviously isn't. I don't need a protractor to see at a glance that none of the angles shown are less than 90 degrees. No clever maths is needed.
Log in to reply
The question isn't asking if the angles match those of the example hexagon. It's asking if it's possible for a circumscribed hexagon to have those internal angles.
If the angles were revised to be 90, 110, 110, 130, 130, 150, which, at first glance, is closer to the diagram, it still wouldn't be possible.
If you had hexagon with angles 60, 80, 120, 130, 160, 170, that hexagon could be circumscribed. (In case you were trying to suggest a hexagon with acute internal angles can't be circumscribed).
In the interest of full disclosure, I also did the quick internal angle sum and got this question wrong.
Log in to reply
Then the picture and question are misleading.
"the measures of the coloured angles" suggests that a protractor is one possible way of answering this.
I initially thought it was the simpler case of checking the sum of the angles which I expected would have not been 720 but then it did turn out to be.
What I hate about some of these problems is that you need a law degree to solve them rather than maths. But in this case "Six points on a circle form a hexagon, as shown in the diagram" can mean nothing else than that the picture shows the actual hexagon in question and it clearly does not have an acute angle hence the provided angles do not match in any order.
The question (as is being answered by most others) should not have had the words "as shown in the diagram" and the picture should definitely have been omitted which would force it to be a much more interesting question requiring more than simple maths - which is why we are here.
Because of the fact that there is an angle of 90 degrees there must be two angles less than 90 degrees. And this is not so.
Can you explain why we must have 2 angles that are less than 90 degrees?
A regular hexagon can be inscribed in a circle, and all of the angles are 1 2 0 ∘ , which refutes your claim that "there must be 2 angles less than 90 degrees".
Can you explain why?
Total sum is 720 and it is hexagon
Log in to reply
If you look at the top solution, showing that "total sum is 720" only allows us to conclude that we have a hexagon. We did not know if this hexagon is cyclic .
What is wrong then
Not in this figure
