Hexagon in Circle in Hexagon
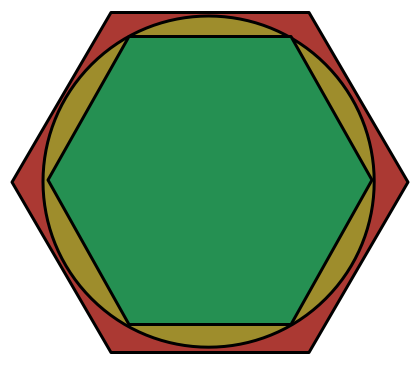 A yellow circle circumscribes a green regular hexagon and is inscribed in a red regular hexagon.
A yellow circle circumscribes a green regular hexagon and is inscribed in a red regular hexagon.
What is the ratio of the areas of the green hexagon to the red hexagon?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
It took me some time to understand what you wrote. I think its far simpler if you would put your word into action like exam paper does.
Label the six vertexes of the red hexagon with A , B , C , D ,E , F
pick any two of them that is adjacent to each other , eg : AB and mark the midpoint as Z
midpoint Z is where the yellow triangle and red hexagon meet by tangent.
-------------------------------------.
draw a line from Z to the origin point of the circle. (OZ)
draw a line from A to the origin point of the circle (OA)
draw a line from B to the origin point of the circle (OB)
-------------------------------------.
given OA , OB , AB are equal length and is equilateral triangle.
Now , you can let AB with any value and attempt to find the OZ
-------------------------------------..
use OZ to calculate area of green hexagon
use AB to calculate area of red hexagon
-------------------------------------..
A r e a o f H e x a g o n = 2 3 3 ( l e n g t h A B )
final ratio 3 : 4
Log in to reply
Yes, you can add that as your own solution!
Log in to reply
It is still the same as Ameya solution. I don't think duplicate this as an individual solution is a good idea.
its like let (x+y = z) as (a+b = c) and claim that (c) is MY unique answer. Maths dont work this way.
Save the solution spaces for other unique solutions. Tq for your kindness tho!
You eyeball the diagram kindly provided, and say, "yeah, that looks like about 3:4"
But if you have to do the math, it's the square of 2 1 3 , which is the ratio of the height and side of an equilateral triangle.
Here is a visual proof: It's probably the "most obvious" dissection scheme. Rotate the green hexagon so that it's touches the red hexagon at the points of tangency. We then easily see how to split the the hexagons up into 1 2 0 ∘ − 3 0 ∘ − 3 0 ∘ triangles.

Yes, looking at the ratio of the height to the hypotenuse is a good way.
Find another "several-line" solution which avoids having to know trigonometry.
Log in to reply
Log in to reply
That's along the right track, but it still requires more seeing/understanding, and ultimately words to express what you're thinking.
Hint: Rotate the green hexagon slightly.
Log in to reply
@Calvin Lin – Here's a graphic with the smaller hexagon rotated

From this one can not only see the 2 1 3 ratio of the height and side of an equilateral triangle, but the method of dissection into 4 identical triangles as suggested by my other graphic, as well (by drawing in some more lines).
Do we observe that the smaller equilateral triangle can be dissected into 3 triangles identical to that small obtuse isosceles triangle, which is another method of dissection?
Log in to reply
@Michael Mendrin – This approach is unique to the hexagon. The issue with the "dissection into 4 identical triangles", is that it doesn't suggest why the remaining red and yellow area is equal to 1 of those triangles.
Almost immediate hint: Draw the center of the equilateral triangle
Log in to reply
@Calvin Lin – "Draw the center of the equilateral triangle"? Are you referring to the other method of dissection I talked about? Hold on for the graphic.
Here it is. It's probably the "most obvious" dissection scheme.

It should be said that the method of dissecting that half of an equilateral triangle into 4 identical right triangles is also unique "to the hexagon". One cannot divide an arbitrary right triangle into 4 identical triangles.
Why can't an arbitrary right triangle be dissected into 4 identical [right] triangles [in the fashion as shown]? Should I ask for a proof of this in a note?
Log in to reply
@Michael Mendrin – Wait, any triangle can be dissected into 4 identical triangles, by connecting up the midpoints. Unless you need them to be oriented the same way?
Did you mean "into 3 identical triangles"? If so, that is a good problem to work on.
Log in to reply
@Calvin Lin – aw you're right about that, fixed it as per your comments
anyway let me try to post a new problem sometime today
If you think about one piece of triangles of the hexagons (one green triangle and one red one) and try to compare it (as the hexagon is regular, so the triangles will be equal), then it will be simple enough. To compare one green triangle w.r.t. one red triangle, you need to express the formula by using a common team (radius of the circle here).
In the green triangle, every side is equal and it's value is equal to the radius of the circle. Don't get it? The two sides of the green triangle is equal to radius of the circle for sure, and the hexagon is regular ... which means, every angle is equal. Got it? Okay, in this case you can get the area of the green triangle easily. Now think about the red triangle, which is also equilateral for sure. Now think the side of the triangle is 'a' and calculate the area. Try to figure out the relationship between 'a' and radius of the circle. It's easy ... huh ?
The ratio of the areas is also the ratio of the squares of the side lengths.
Let's just calculate half the side length as the ratio is unchanged and it's easier to find.
We can calculate the side lengths with a little bit of trig by drawing a line through the centre of the circle and perpendicular to one of the sides of both hexagons.
We have created two right angle triangles. They share the same angle of 6 π radians.
l 1 = r sin ( 6 π )
l 2 = r tan ( 6 π )
∴ A 2 A 1 = l 2 2 l 1 2 = cos 2 ( 6 π ) = 4 3
r is the radius although it doesn't change anything. l 1 represents half the length of one side of the smaller hexagon. l 2 represents half the length of one side of the larger hexagon.
Bonus : generalise for regular polygons with n sides.
There is a "one-line" solution to this problem :)
Log in to reply
What is that one-line??
Log in to reply
I was trying all last night to find it. After seeing the beautiful triangle solution where you rotate one triangle, I tried to do the same thing here but couldn't do it. I would love to be enlightened by Calvin.
Log in to reply
@Isaac Buckley – I was referring to this image that Michael drew

You can see how 1/6 of the green hexagon corresponds to 3 1 2 0 ∘ − 3 0 ∘ − 3 0 ∘ triangles, while 1/6 of the red hexagon corresponds to 4 of them.
Log in to reply
@Calvin Lin – Yes :) I just noticed it. Very nice!
Let Side of big hexagon is A Then side of small hexagon will be A√3/2 Then the ratio of area 3:4
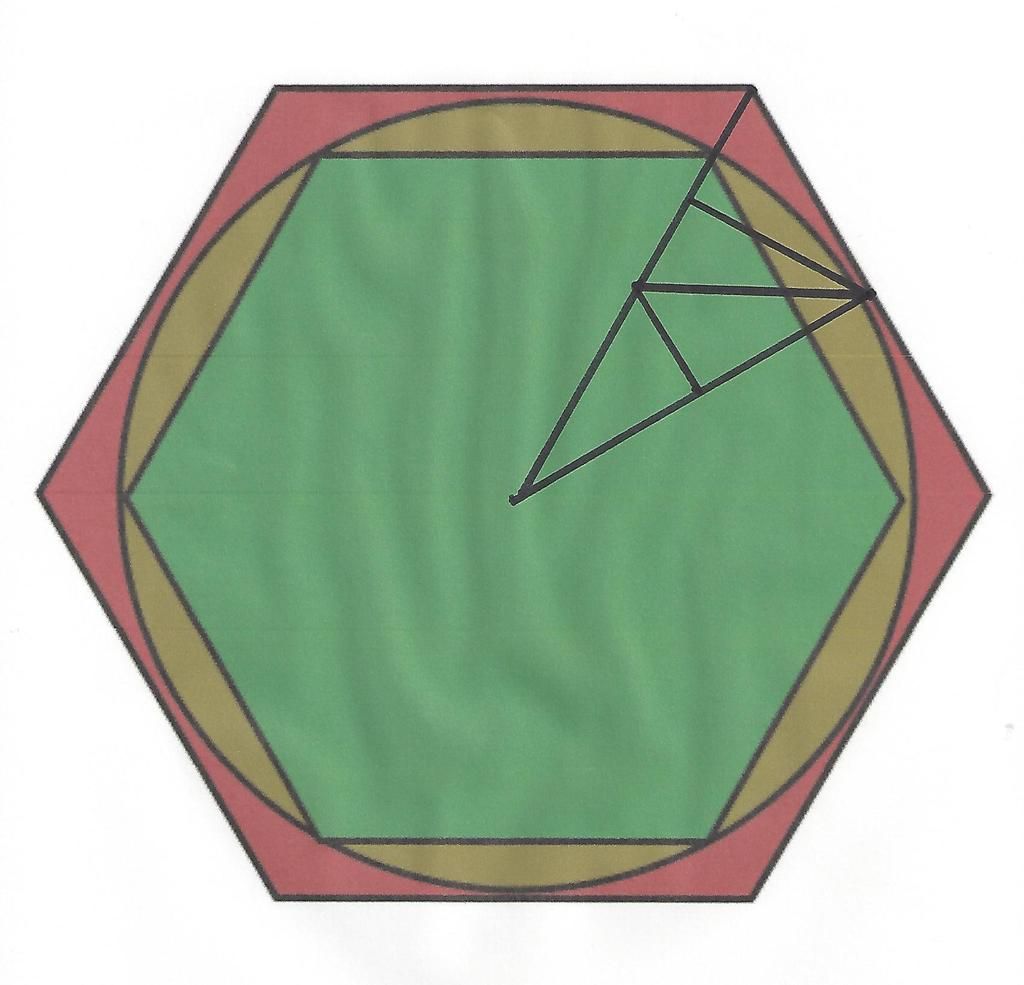
just a simple solution.. can do it orally...
the hexagons are regular all the sides and the line joining the center to any vertex are equal...
so, the area of hexagon will be area of 6 equilateral triangles... the, side of the green hexagon will be equal to the radius of the circle which forms a right angle triangle with the side of the red hexagon as it's hypotenuse...
so, ratio will be ,