Hexagon in Triangle
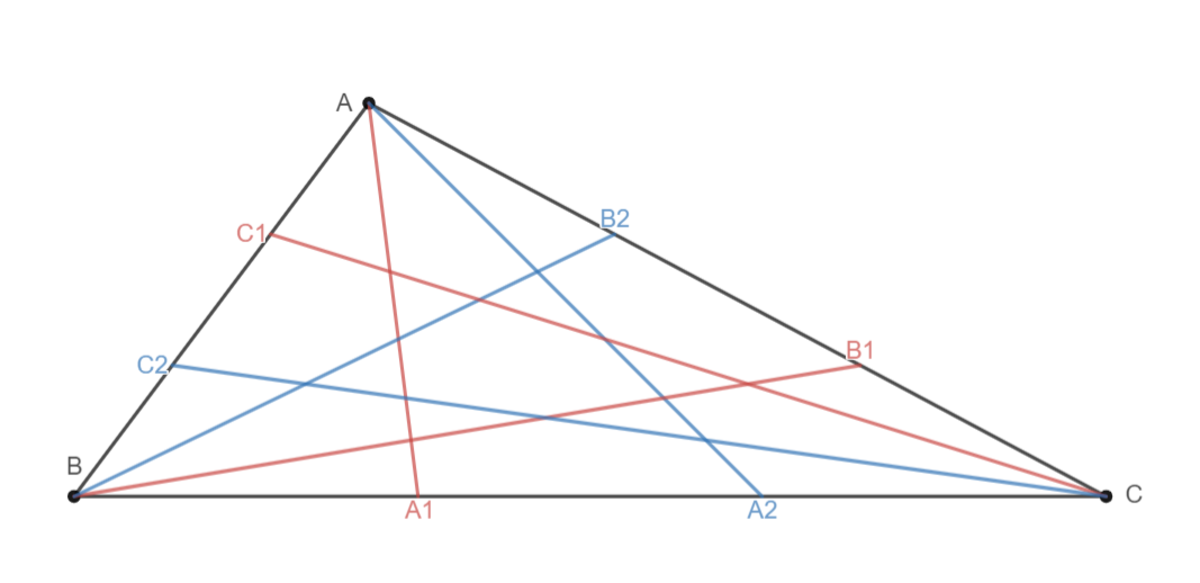 Six cevians are drawn as shown in figure above. These cevians form a hexagon in the middle of triangle. Cevians are such that
Six cevians are drawn as shown in figure above. These cevians form a hexagon in the middle of triangle. Cevians are such that
B C B A 1 = C A C B 1 = A B A C 1 = p
B C B A 2 = C A C B 2 = A B A C 2 = q with 0 < p < q < 1
If for p = 0 . 1 and some q ,
area of △ A B C area of hexagon = 0 . 7
Find q and submit ⌈ 1 0 0 0 0 0 q ⌉
The answer is 97429.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
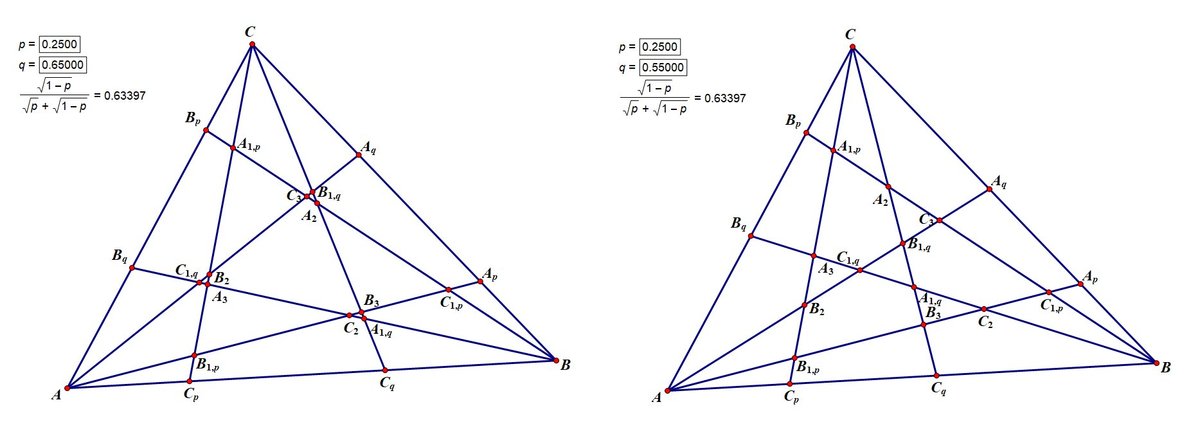
Great solution using trilinear coordinates. Your expression of area of hexagon in terms of p and q is correct. But I think condition for existence of hexagon is wrong. You said for any given p , q must be such that p + 1 1 < q < 1 for the existence of hexagon. But take an example of p = 0 . 2 5 and q = 0 . 6 5 , hexagon is formed but this p and q do not satisfy your condition. I don't know how to post photos in comment otherwise I would have shown it to you. But I am giving you a link of desmos graphing calculator - https://www.desmos.com/calculator/lrrnzwoxjg . You can see there how hexagon is varying with p and q .
Log in to reply
You are right. I have corrected the critical value for q to its actual value of p + 1 − p 1 − p . The following pictures show what happens either side of the critical value for p = 0 . 2 5 .
Log in to reply
There is also an upper bound on q in terms of p. Try to find out.
Log in to reply
@Shikhar Srivastava – Fixed that one, too. Of course, we need all six "little" triangles in order to have a hexagon.
Log in to reply
@Mark Hennings – Yaah! Now that's correct. Well your approach of using trilinear coordinates is good. I have used only elementary geometry which was quite time taking.
Log in to reply
@Shikhar Srivastava – It is worth noting that one implication of the inequality giving the valid range of q is that p < 2 1 .
Log in to reply
@Mark Hennings – Yes, and if we remove the constraint p < q then we see that for any given p value of should be in between 1 − p + p 1 − p and ( 1 − p ) 2 + p 2 ( 1 − p ) 2 . First expression is the lower bound of q when p < 2 1 and upper bound of q when p > 2 1 . Similarly the second expression is upper bound when p < 2 1 and lower bound when p > 2 1 . This is described in the figure below.
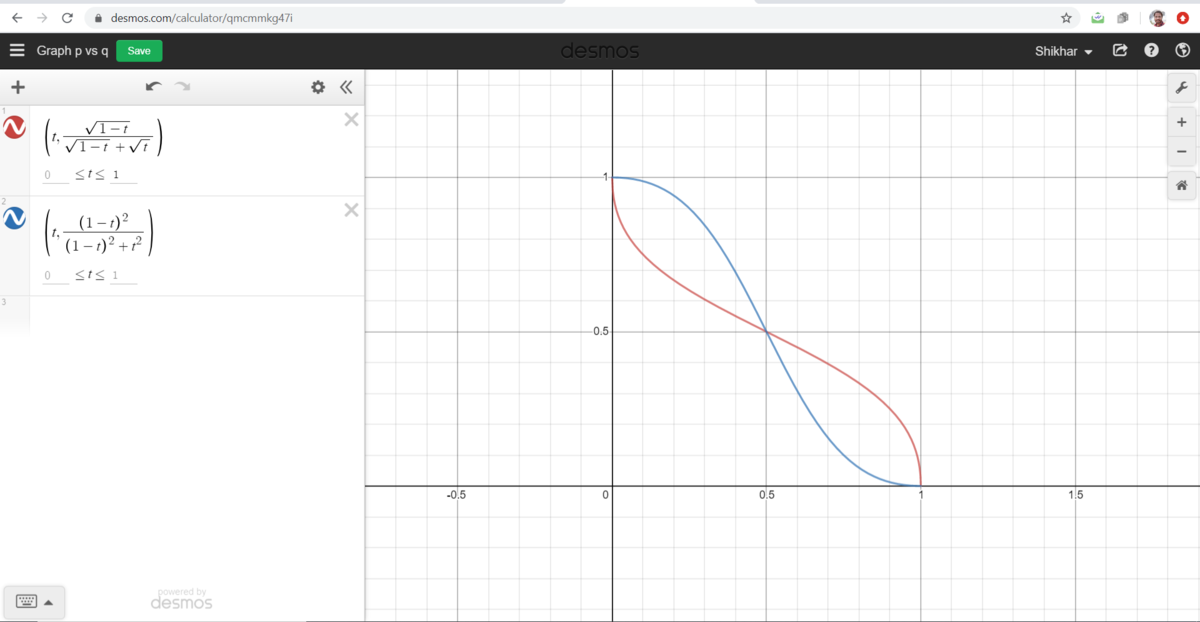
In the graph x axis is p , y-axis is q and curves are the limit. We also infer that p and q cannot be both less than 2 1 and cannot be both greater than 2 1 .
The only way I know to post a picture in a comment is to open up one of your own solutions, post a picture there, copy the resulting hyperlink, get out of your own solution, and paste the hyperlink into the comment!
There exists an analytical method for finding out q . The value of q is 7 3 9 7 2 0 .
Log in to reply
Of course, since the necessary equation is simply a quadratic in q , and we can ignore the second solution of q = 1 .
This problem is extremely suitable for the use of
Routh's theorem
.
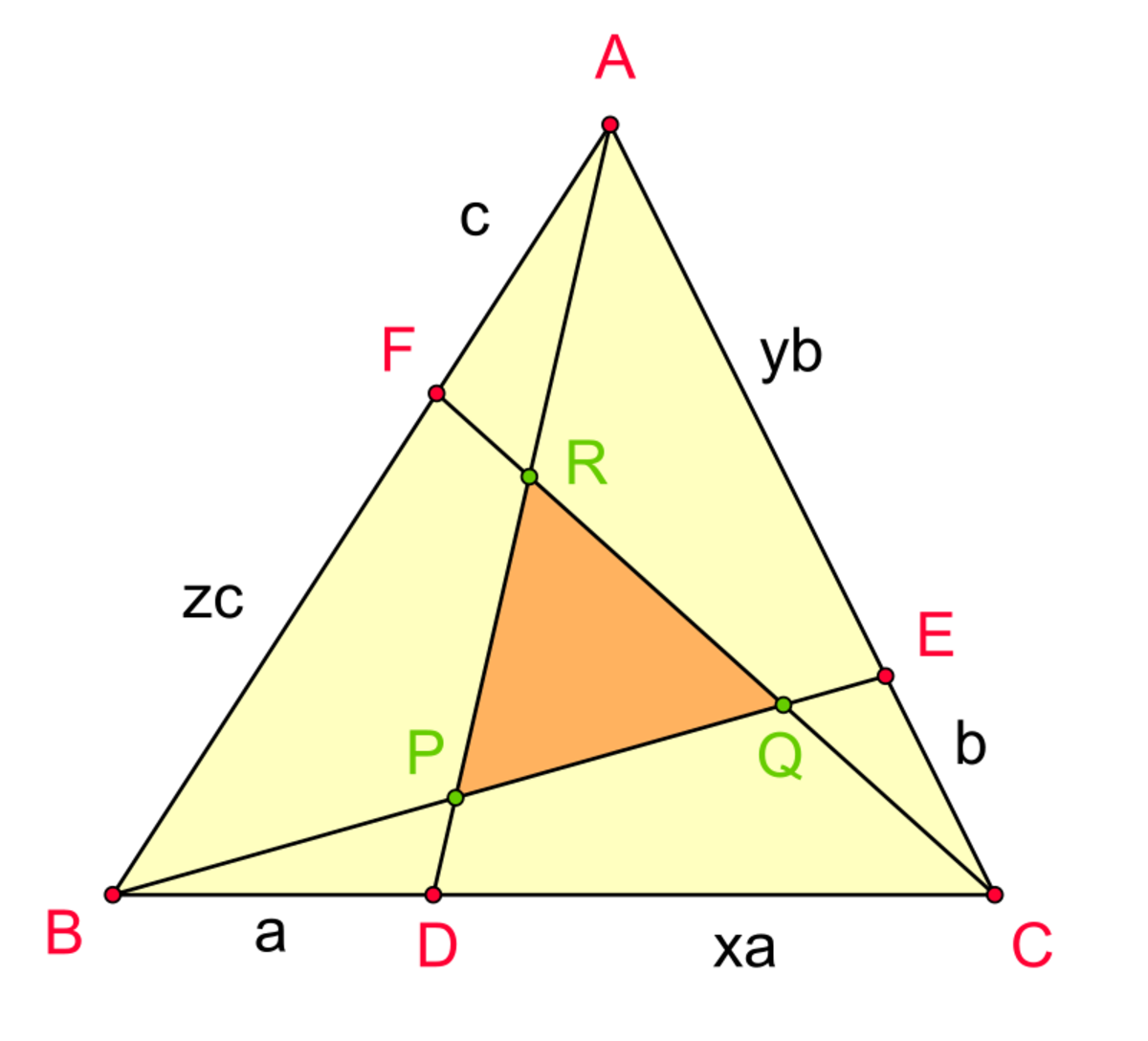 Routh's theorem
Routh's theorem
The ratio of the area of a cevian triangle to the original triangle depicted above is ( x y + y + 1 ) ( y z + z + 1 ) ( z x + x + 1 ) ( x y z − 1 ) 2
Now, let's go back to the triangle of our problem. We will first find the area of the red triangle and then subtract the areas of of the smaller triangles around its vertices to get the area of the hexagon. It should be noted that the three smaller triangles whose areas are to be subtracted have equal areas.
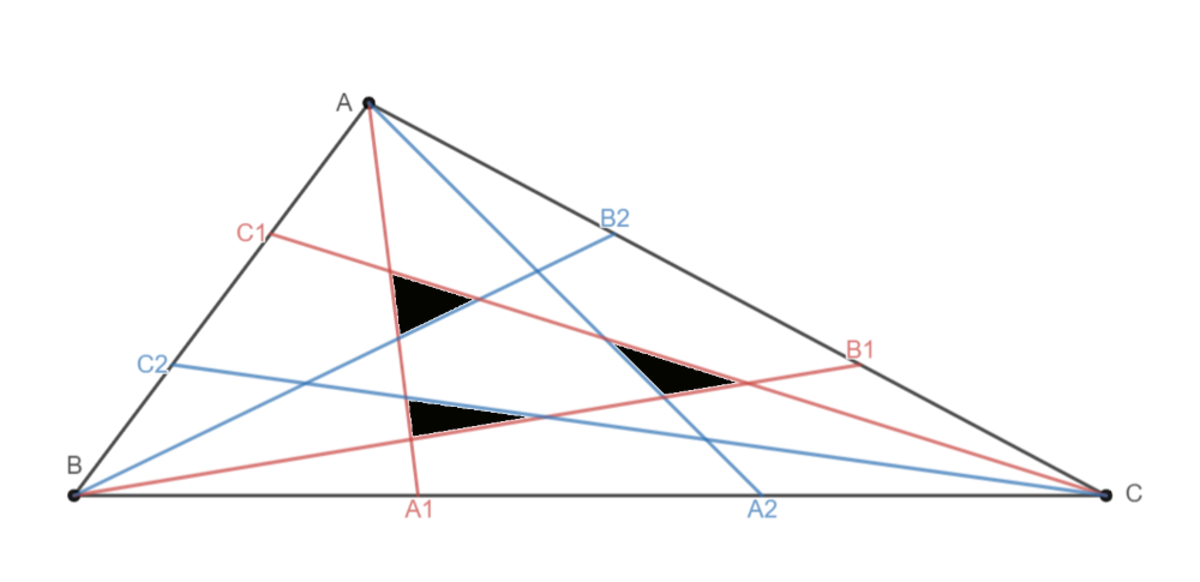 Our problem
Our problem
Here, B C B A 1 = 1 0 1 ⟹ B A 1 A 1 C = 9
Let's assume B A 2 A 2 C = x ⟹ B C B A 2 = q = 1 + x 1
Now, we get the following equation. ( 9 2 + 9 + 1 ) 3 ( 9 3 − 1 ) 2 − ( 9 x + 1 0 ) ( 8 1 + 1 0 ) ( 1 0 x + 1 ) 3 ( 8 1 x − 1 ) 2 = 1 0 7 This simplifies to x = 7 2 0 1 9
Therefore, q = 1 + x 1 = 7 3 9 7 2 0
Nice solution.You genius
Brilliant Solution. Short and simple.
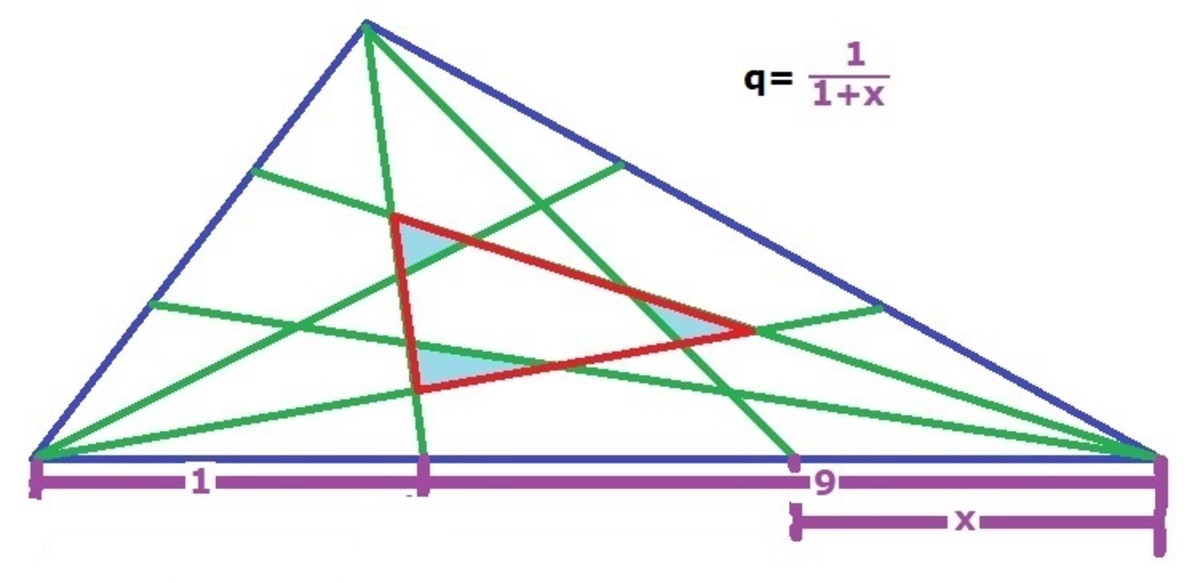 Just to make it easy.
Just to make it easy.
The triangle can be stretched and skewed to an equilateral triangle with unit sides and still preserve the ratio of areas. Placing B at the origin and C at ( 1 , 0 ) , then A is ( 2 1 , 2 3 ) , O is ( 2 1 , 6 3 ) , A 1 is ( 1 0 1 , 0 ) , A 2 is ( q , 0 ) , B 1 is ( 2 0 1 9 , 2 0 3 ) , C 1 is ( 2 0 9 , 2 0 9 3 ) , and C 2 is ( 2 1 ( 1 − q ) , 2 3 ( 1 − q ) ) .
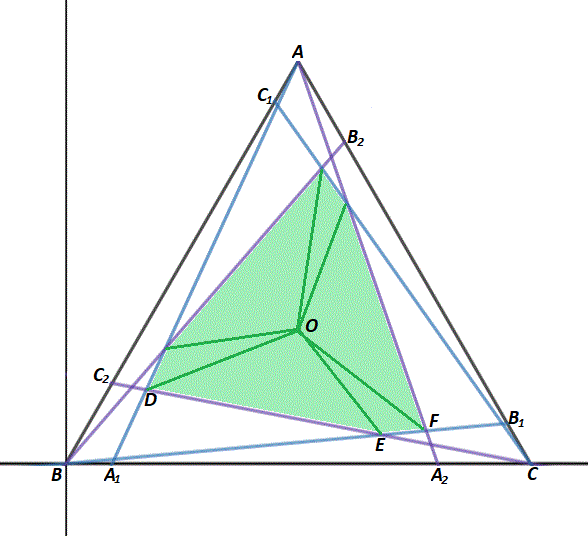
The equation of the line B B 1 is y = 2 3 x , the line C C 2 is y = q + 1 3 ( q − 1 ) ( x − 1 ) , the line A A 1 is y = 4 5 3 ( x − 1 0 1 ) , and the line A A 2 is y = 1 − 2 q 3 ( x − q ) .
A A 1 and C C 1 intersect at D ( 2 q + 1 8 9 − 7 q , 2 q + 1 8 9 3 − 9 3 q ) , A A 1 and B B 1 intersect at E ( 1 8 q − 2 0 1 9 q − 1 9 , 1 8 q − 2 0 3 q − 3 ) , and A A 2 and B B 1 intersect at F ( 2 q + 1 8 1 9 q , 2 q + 1 8 3 q ) .
The area of △ D O E is A △ D O E = 2 1 ( ( D x − O x ) ( E y − O y ) − ( E x − O x ) ( D y − O y ) ) = 1 0 8 q 2 + 8 5 2 q − 1 0 8 0 1 6 4 3 q 2 − 2 4 4 3 q + 8 1 3 and the area of △ E O F is A △ D O E = 2 1 ( ( E x − O x ) ( F y − O y ) − ( F x − O x ) ( E y − O y ) ) = 2 7 q 2 + 2 1 3 q − 2 7 0 1 6 3 q 2 − 3 6 3 q + 1 8 3 .
The area of △ A B C is A △ A B C = 4 3 and by symmetry the area of the hexagon is 3 ( A △ D O E + A △ E O F ) , and since area of △ABC area of hexagon = 0 . 7 , we have 4 3 3 ( 1 0 8 q 2 + 8 5 2 q − 1 0 8 0 1 6 4 3 q 2 − 2 4 4 3 q + 8 1 3 + 2 7 q 2 + 2 1 3 q − 2 7 0 1 6 3 q 2 − 3 6 3 q + 1 8 3 ) = 1 0 7 , which rearranges to 7 3 9 q 2 − 1 4 5 9 q + 7 2 0 = 0 and solves to q = 7 3 9 7 2 0 for q < 1 .
Therefore, ⌈ 1 0 0 0 0 0 q ⌉ = ⌈ 1 0 0 0 0 0 ⋅ 7 3 9 7 2 0 ⌉ = 9 7 4 2 9 .
This question is most easily handled using trilinear coordinates. The triangle vertices A , B , C have coordinates A : 1 : 0 : 0 B : 0 : 1 : 0 C : 0 : 0 : 1 while the points A p , A q . B p , B q , C p , C q where B A p = p B C and B A q = q B C (and similarly for the other four points) have coordinates A p : A q : 0 : ( 1 − p ) c : p b 0 : ( 1 − q ) c : q b B p : B q : p c : 0 : ( 1 − p ) a q c : 0 : ( 1 − q ) a C p : C q : ( 1 − p ) b : p a : 0 ( 1 − q ) b : q a : 0 The points A 1 , p , A 1 , q , B 1 , p , B 1 , q , C 1 , p , C 1 , q can now be calculated. A 1 , p is the intersection of B B p and C C p , while A 1 , q is the intersection of B B q and C C q , with the other four points similarly defined. Solving the trilinear equations for the intersection of these lines, we obtain the coordinates A 1 , p : B 1 , p : C 1 , p : p ( 1 − p ) b c : p 2 a c : ( 1 − p ) 2 a b ( 1 − p ) 2 b c : p ( 1 − p ) b c : p 2 a b p 2 b c : ( 1 − p ) 2 a c : p ( 1 − p ) a b A 1 , q : B 1 , q : C 1 , q : q ( 1 − q ) b c : q 2 a c : ( 1 − q ) 2 a ( 1 − q ) 2 b c : q ( 1 − q ) b c : q 2 a b q 2 b c : ( 1 − q ) 2 a c : q ( 1 − q ) a b Similarly, the points A 2 , A 3 , B 2 , B 3 , C 2 , C 3 can be determined, where A 2 is the intersection of B B p with C C q , while A 3 is the intersection of B B q with C C p (and the other four points are similarly defined). We obtain A 2 : B 2 : C 2 : p ( 1 − q ) b c : p q a c : ( 1 − p ) ( 1 − q ) a b ( 1 − p ) ( 1 − q ) b c : p ( 1 − q ) a c : p q a b p q b c : ( 1 − p ) ( 1 − q ) a c : p ( 1 − q ) a b A 3 : B 3 : C 3 : ( 1 − p ) q b c : p q a c : ( 1 − p ) ( 1 − q ) a b ( 1 − p ) ( 1 − q ) b c : ( 1 − p ) q a c : p q a b p q b c : ( 1 − p ) ( 1 − q ) a c : ( 1 − p ) q a b
This construction will not result in a central hexagon unless q is large enough. A hexagon will be formed so long as A 1 , q lies inside the triangle A B A p , B 1 , q lies inside the triangle B C B p and C 1 , q lies inside the triangle C A C p . Symmetry gives us that these three things either all occur at the same time, or none occur. Thus the critical case to consider is when A 1 , q lies on the line A A p , which occurs when A 1 , q = B 3 = C 2 . This implies that p ( 1 − q ) = λ p q , p q = λ ( 1 − p ) ( 1 − q ) and ( 1 − p ) ( 1 − q ) = λ ( 1 − p ) q for some λ > 0 , which tells us that q = p + 1 − p 1 − p Equally well, for there to be an internal hexagon, the point A 1 , p has to lie in the triangle A A q C , the point B 1 , p has to lie in the triangle B B q A , and the point C 1 , p has to lie in the triangle C C q B . Again, these three things either all happen, or none of them happen; the critical case to consider is when A 1 , p lies on A A q , which occurs when A 1 , p = B 2 = C 3 . The condition for this is q = p 2 + ( 1 − p ) 2 ( 1 − p ) 2 We only have an internal hexagon when p + 1 − p 1 − p < q < p 2 + ( 1 − p ) 2 ( 1 − p ) 2 . Note that this requires that 0 < p < 2 1 . Then the area of the internal hexagon is equal to the area of the triangle A 1 , p B 1 , p C 1 , p minus the areas of the triangles A 1 , p B 2 C 3 , B 1 , p C 2 A 3 and C 1 , p A 2 B 3 . Standard formulae for the areas of triangles given by trilinear coordinates tell us that the last three triangles all have the same area, and that the area of the internal hexagon is ( 1 − p + p 2 ) 3 Δ ∣ ∣ ∣ ∣ ∣ ∣ p ( 1 − p ) ( 1 − p ) 2 p 2 p 2 p ( 1 − p ) ( 1 − p ) 2 ( 1 − p ) 2 p 2 p ( 1 − p ) ∣ ∣ ∣ ∣ ∣ ∣ − ( 1 − p + p 2 ) ( 1 − p + p q ) ( 1 − q + p q ) 3 Δ ∣ ∣ ∣ ∣ ∣ ∣ p ( 1 − p ) ( 1 − p ) ( 1 − q ) p q p 2 p ( 1 − q ) ( 1 − p ) ( 1 − q ) ( 1 − p ) 2 p q ( 1 − p ) q ∣ ∣ ∣ ∣ ∣ ∣ which simplifies to give ( 1 − p + p q ) ( 1 − q + p q ) − 2 + 5 ( p + q ) − 3 ( p 2 + 4 p q + q 2 ) + 8 p q ( p + q ) − 8 p 2 q 2 Δ for p + 1 − p 1 − p < q < p 2 + ( 1 − p ) 2 ( 1 − p ) 2 , where Δ is the area of the original triangle A B C .
If we consider the expression for the area of the internal hexagon with p = 0 . 1 and for 0 . 9 + 0 . 1 0 . 9 = 4 3 < q < 8 2 8 1 = 0 . 1 2 + 0 . 9 2 0 . 9 2 , we obtain, solving a quadratic equation for q - thank you, @Atomsky Jahid ) a relative area of 0 . 7 for the internal hexagon when q = 7 3 9 7 2 0 , and hence ⌈ 1 0 5 q ⌉ = 9 7 4 2 9 .