Hexagonal Checkers 2
In an infinitely large triangular peg board game, the goal is to get a peg into the top space on the board through a series of moves. A move consists of a peg jumping over an adjacent peg, which eliminates the peg which was jumped over.
It is possible to get a peg into the top space when all the starting pegs are below the 2 nd row. This starting orientation is shown below.
What is the largest possible n such that we can get a peg into the top space when all the starting pegs are below the n th row?
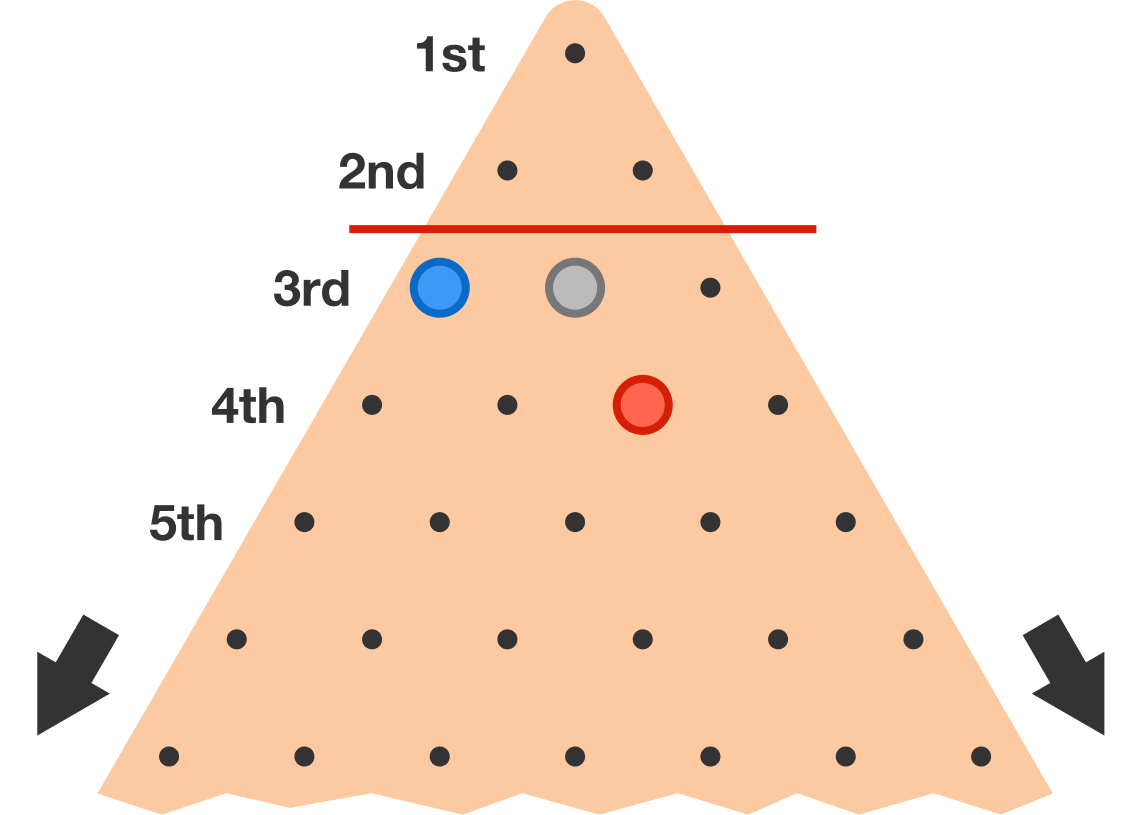 Red jumps Grey, then Blue jumps Red. This puts Blue into the top space.
Red jumps Grey, then Blue jumps Red. This puts Blue into the top space.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
can you give detailed explanation? i thought of so many ways to solve this problem. but i could not succeed.
Log in to reply
Which part of my proof did you not understand?
Log in to reply
thanks. now i understood. just i want to know how did you get this idea. i feel it is impossible to solve this unless someone has done something similar before. there may be some extraordinary people who can get it without any previous experience of solving something similar. thanks for the solution.
Log in to reply
@Srikanth Tupurani – Yes, this proof is hard to come by out of the blue. This might be the thought process of someone trying to solve this. We need to notice that checkers down low are somehow less helpful than checkers up high (because it takes two low checkers to make a high one). Specifically a checker on the nth row must somehow be equivalent to one on the n+1th row and one on the n+2nd row. We can guess that we can use a monoinvariant to quantify how useful (or how high we can get) a given state of the game is. We need to further guess that our monoinvariant will be the sum of all the "usefulness values" of checkers on the board where the usefulness of a checker is large near the top and smaller near the bottom. Our usefulness values also have to get small quickly enough such that the infinite sum of all usefulness values needs to converge. One way to do this would be to use a geometric series according to the row that each checker is in. In order for our monoinviariant to be of any use, we need to choose a common ratio such that r n = r n + 1 + r n + 2 . This tells us that a common ratio of the inverse golden ratio might work. From there it is straightforward. I hope this helps you better understand how this proof was come about. Numberphile has a video on a similar type of proof that may be helpful. https://www.youtube.com/watch?v=Or0uWM9bT5w
Log in to reply
@John Ross – thanks for explanation. this is an amazing problem.
Log in to reply
@Srikanth Tupurani – Thank you. I like this problem too.
There are two entertaining videos on numberphile solving the harder problem known as 'Conway's checkers'. If you watch them first it will be easy to understand John's proof.
For this problem, is the number of checkers unlimited?
"Finding the solution backwards" is the easiest way to deal with this. We are reasonably confident that there is sufficient space, and just need to keep on pushing downwards. If we were unable to keep on pushing downwards, then this will introduce some new constraint, which we can use to update the values of the cell.
Here is one solution for n = 6:
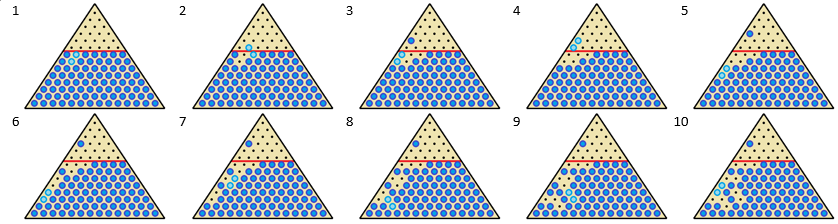
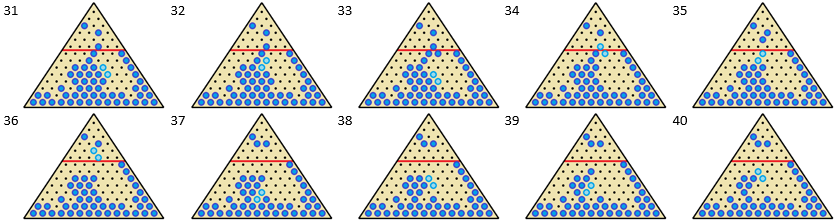
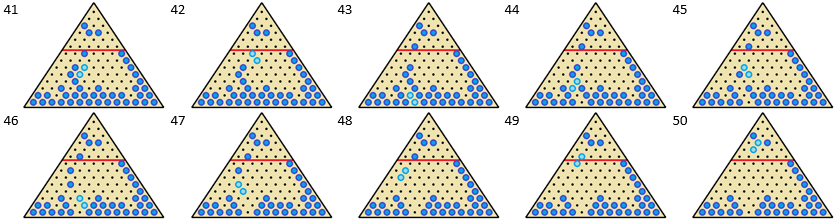

This is the Pablito's army variant of Conway's soldiers . The maximum number of empty rows for this variant is 6 .
Thank you for pointing that out. I made this variation up on my own, so I didn't know that it already had a name. I saw a proof of Conway's Soldiers and played around with different versions, until I found this variation. I am curious about this type of problem, so I will try to do some more research about solved variations. Do you know if my other variation already has a name? (link in my solution)
thanks. it is amazing
Thanks! Always happy to have a name to go along with a problem.
This is not a full solution, and is designed to expand on John Ross's solution. We want to put an number in each position such that the sum of all positions is finite, and yet, when you take the sum of all populated positions, making any move strictly increases, or strictly decreases the sum. This sum will then take on the role of a characteristic value, which we can use to prove impossibility.
The easiest way to populate the cells with these numbers is to put 1 at the top, and then for each subsequent row, put the value of any individual position on the previous row, multiplied by some x, where ∣ x ∣ < 1 . Now, suppose that we make a move that takes a peg from two rows and places it on the row above. We can define our numbers such that doing this does not alter the characteristic value. In this case, it follows that x 2 + x = 1 . Solving with the quadratic equation gives us two candidate solutions, x = 2 5 − 1 and x = 2 − 5 − 1 . Looking back to our restriction, ∣ x ∣ < 1 we can discard the second possibility, leaving just one possible x value, 2 5 − 1 . This value may look familiar, as it is related to the golden ratio - in fact, it is the reciprocal of phi.
To check that the characteristic value is valid, we consider all possible moves. Moving up does not change the characteristic value, but moving sideways or down will decrease the characteristic value, which means that it can be used to prove impossibility.
To start, we place the number r n − 1 into each cell, where n is the row that the cell is in and r = 2 5 − 1 . We then define the characteristic value of each state of the game to be the sum of all the cells that have a checker on them. Notice that for each move, the characteristic value either stays the same or decreases (this is true because r n + 2 + r n + 1 = r n .) In other words the characteristic value at the beginning of a game will be greater than or equal to the characteristic value at the end of the game. The characteristic value of the desired state (a checker in the top cell) is 1 . We notice by the formula for the arithmetico-geometric sequence that the characteristic value for a checkerboard with all the cells filled would be 2 7 + 3 5 ≈ 6 . 8 5 4 If the line were below the seventh row, the maximum possible characteristic value for the beginning state would be 2 − 8 1 + 3 1 5 ≈ . 8 6 7 Therefore it is impossible to get a checker into the top cell when n = 7 . The n = 6 case can be shown by example. See also a variation on this problem: Hexagonal Checkers .
Note: Unfortunately, when I found the n = 6 case by hand, it took me too many moves to be short enough to share here. If you would like to verify the n = 6 case for yourself please go ahead and do so. I would recommend finding the solution backwards (i.e. starting with the top cell filled and replacing one checker with two checkers in the appropriate manner until you get all checkers below the sixth row). Also, if you find it easier, you can notice that the game on a triangular board is equivalent to the game on one quadrant of a square board.
Edit: The question has been rephrased from checkers on a triangular checkerboard to pegs in a triangular pegboard, so that is why my solution uses the original terminology.