HexaRatio
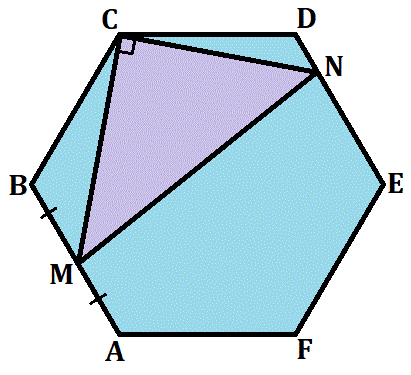
If right △ M C N is inscribed in regular hexagon A B C D E F such that M is the midpoint of A B , then the ratio of the perimeters of pentagon A M N E F to hexagon A B C D E F is b a for relatively prime positive integers a and b .
Find a + b .
Challenge: Solve without using trigonometry.
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Good solution. I think there is a typo: "reflect △ M B C " instead of " △ A B C ".
My approach was based on 3D coordinate geometry. Why 3D? Because this enables us to simplify the numbers based on the fact that, if you cut a cube in half perpendicularly to a vertex axis, the cross-section so produced is a regular hexagon.
So let the coordinates be as follows: A = ( 0 , − 2 , − 2 ) B = ( − 2 , 0 , − 2 ) C = ( − 2 , 2 , 0 ) D = ( 0 , 2 , 2 ) E = ( 2 , 0 , 2 ) F = ( 2 , − 2 , 0 ) M = ( − 1 , − 1 , − 2 ) N = ( t , 2 − t , 2 ) The dot product of non-zero vectors is zero if and only if they are perpendicular. Thus we can solve: C M . C N = 0 ⇒ ⎝ ⎛ 1 − 3 − 2 ⎠ ⎞ . ⎝ ⎛ t + 2 − t 2 ⎠ ⎞ = 0 ⇒ ( 1 ) ( t + 2 ) + ( − 3 ) ( − t ) + ( − 2 ) ( 2 ) = 0 ⇒ 4 t − 2 = 0 ⇒ t = 2 1 This gives N = ( 2 1 , 2 3 , 2 ) .
Now we can calculate the perimeters of the two shapes. Perimeter of hexagon: h = 6 A F = 6 8 = 1 2 2 Perimeter of pentagon: p = A M + M N + N E + E F + F A = 2 + 2 7 2 + 2 3 2 + 2 ( 2 2 ) = 1 0 2 Ratio: p h = 1 0 2 1 2 2 = 5 6 .
Wow, nice out-of-the-box (or maybe I should say out-of-the-cube) solution!
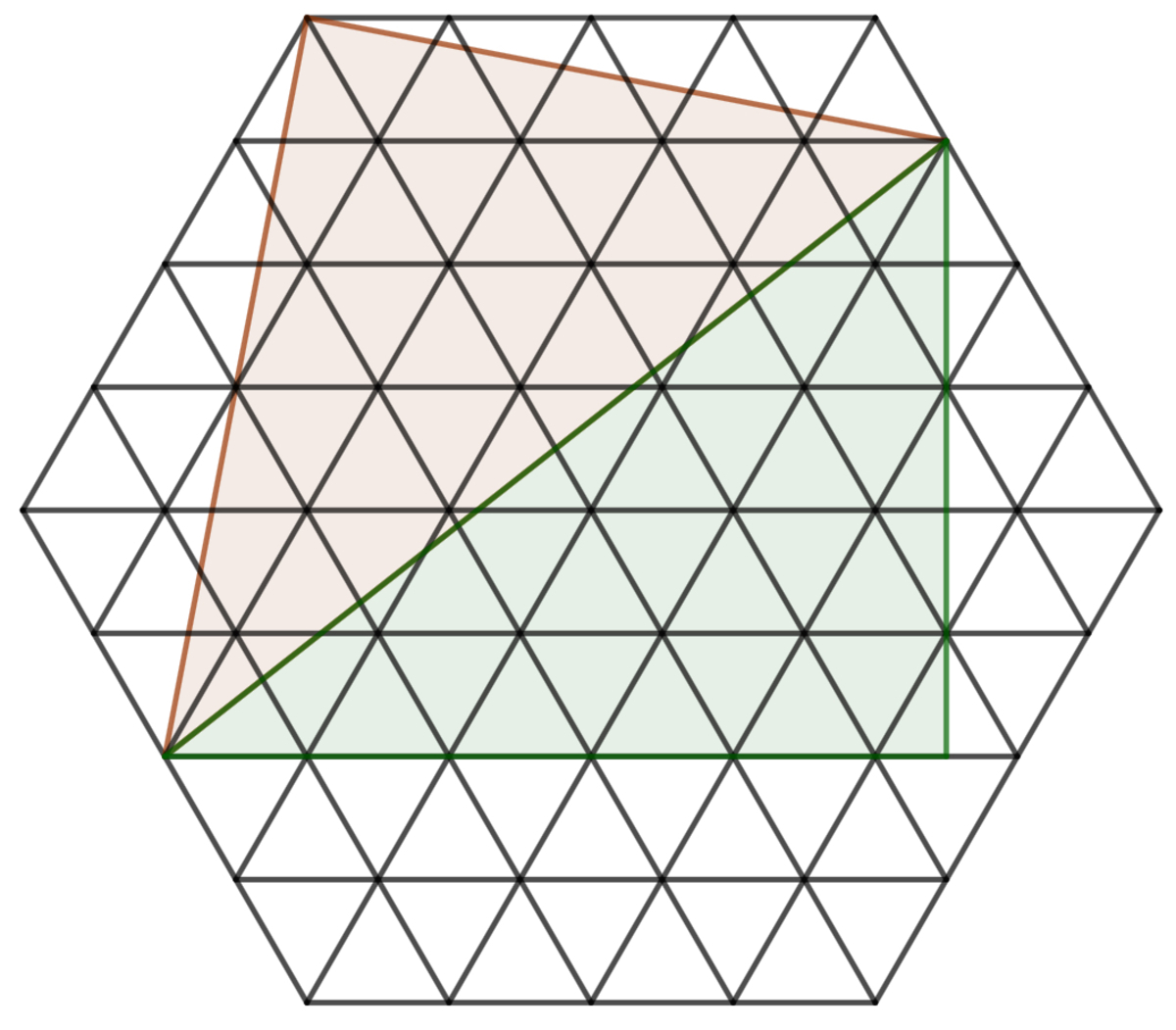
The unit hexagon can be presented in the lattice points of unit equilateral triangle as shown above. Notice that by extending the leg perpendicular to one of the segments, we have a right green triangle with leg lengths 2 1 1 and 2 5 3 . Following Pythagorean’s Theorem, ( 2 1 1 ) 2 + ( 2 5 3 ) 2 = 7 . Therefore,
Perimeter of 6-gon Perimeter of 5-gon = 4 × 6 2 + 3 + 4 + 4 + 7 = 6 5
which returns us a + b = 5 + 6 = 1 1 .
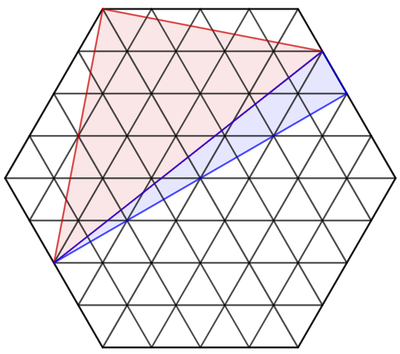
Note that if we extend the segment as shown above, it is easier to see that the right triangle of side lengths 1 and 2 3 × 8 = 4 3 = 4 8 has the hypotenuse 4 9 = 7 .
From the tell of the diagram I provided, there exists different ways of proving the hypotenuse length of the given right triangle is 7 . I have updated my solution, which includes the alternate way of noticing the side length 7 . It appears that some original/fresh question ideas popped up in my head after I inspected my own solution! What a luck!
Here is the follow-up problem I posted. It adds some nice twist from my solution. :)
@Michael Huang - Hi Michael! In both your solution you take for granted that the brown triangle (red in the second solution) formed by the specific three vertex points is indeed a right triangle. Isn't it necessary to prove this? Do I miss something obvious here?
Log in to reply
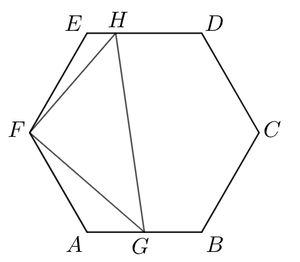
Ah. That is a good question. The diagrams I showed are some interpretations of the problem. There is some combinatorial billiard feeling to the problem, but if suppose we use elementary geometry, it is good enough to prove that given G is a midpoint of A B , ∣ E H ∣ ∣ A G ∣ = 2 (I set my variables for this one), which is rational. In this case, as we are considering a regular hexagon, we can extend triangular lattice points.
Log in to reply
I see, but how to prove that this ratio equals 2? Check my solution, based on elementary euclidean geometry.
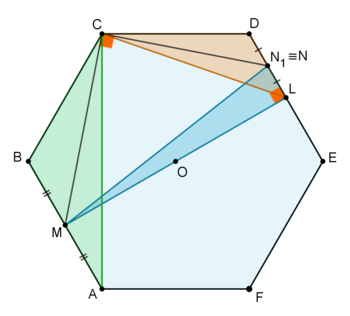 For simplicity we scale
A
B
C
D
E
F
to a unit hexagon. Then
A
C
is the side of an equilateral triangle inscribed in the hexagon’s (unit) circumsircle, thus,
A
C
=
3
.
Let
L
be the midpoint of
D
E
and
N
1
the midpoint of
D
L
.
For simplicity we scale
A
B
C
D
E
F
to a unit hexagon. Then
A
C
is the side of an equilateral triangle inscribed in the hexagon’s (unit) circumsircle, thus,
A
C
=
3
.
Let
L
be the midpoint of
D
E
and
N
1
the midpoint of
D
L
.
First we prove that
N
1
in fact is the given point
N
.
By
Apollonius's Theorem
on
△
A
B
C
,
C
B
2
+
C
A
2
=
2
{
C
M
2
+
(
2
A
B
)
2
}
from which we get
C
M
2
=
4
2
C
B
2
+
2
C
A
2
−
A
B
2
=
4
2
×
1
2
+
2
×
3
2
−
1
2
=
4
7
Similarly, for the median
C
N
1
of
△
C
D
L
,
C
N
1
2
=
4
2
C
D
2
+
2
C
L
2
−
D
L
2
=
4
2
C
D
2
+
2
C
M
2
−
D
L
2
=
4
2
×
1
2
+
2
×
4
7
−
(
2
1
)
2
=
1
6
2
1
By Pythagorean theorem on right
△
M
L
N
1
,
M
N
1
2
=
M
L
2
+
L
N
1
2
=
(
2
O
L
)
2
+
(
2
D
L
)
2
=
(
2
⋅
2
3
)
2
+
(
4
1
)
2
=
1
6
4
9
thus
M
N
1
=
4
7
We notice that
C
M
2
+
C
N
1
2
=
4
7
+
1
6
2
1
=
1
6
4
9
=
M
N
1
2
Hence, by the converse of Pythagorean theorem (
Euclid's Elements, Book I, Proposition 48
),
∠
M
C
N
1
=
9
0
∘
and this proves that
N
1
coincides with given point
N
.
The perimeter P 5 of pentagon A M N E F is P 5 = A M + M N + N E + E F + F A = 2 1 + 4 7 + 4 3 + + 1 + 1 = 5 and the perimeter P 6 of the regular hexagon is 6, hence, P 6 P 5 = 6 5 For the answer, a = 5 , b = 6 , thus, a + b = 1 1 .
Original (trig) solution in a comment below.
Say the hexagon has unit sides. Note that
A
B
and
D
E
are parallel. To make things a bit easier to see, rotate the image so that these lines are horizontal:
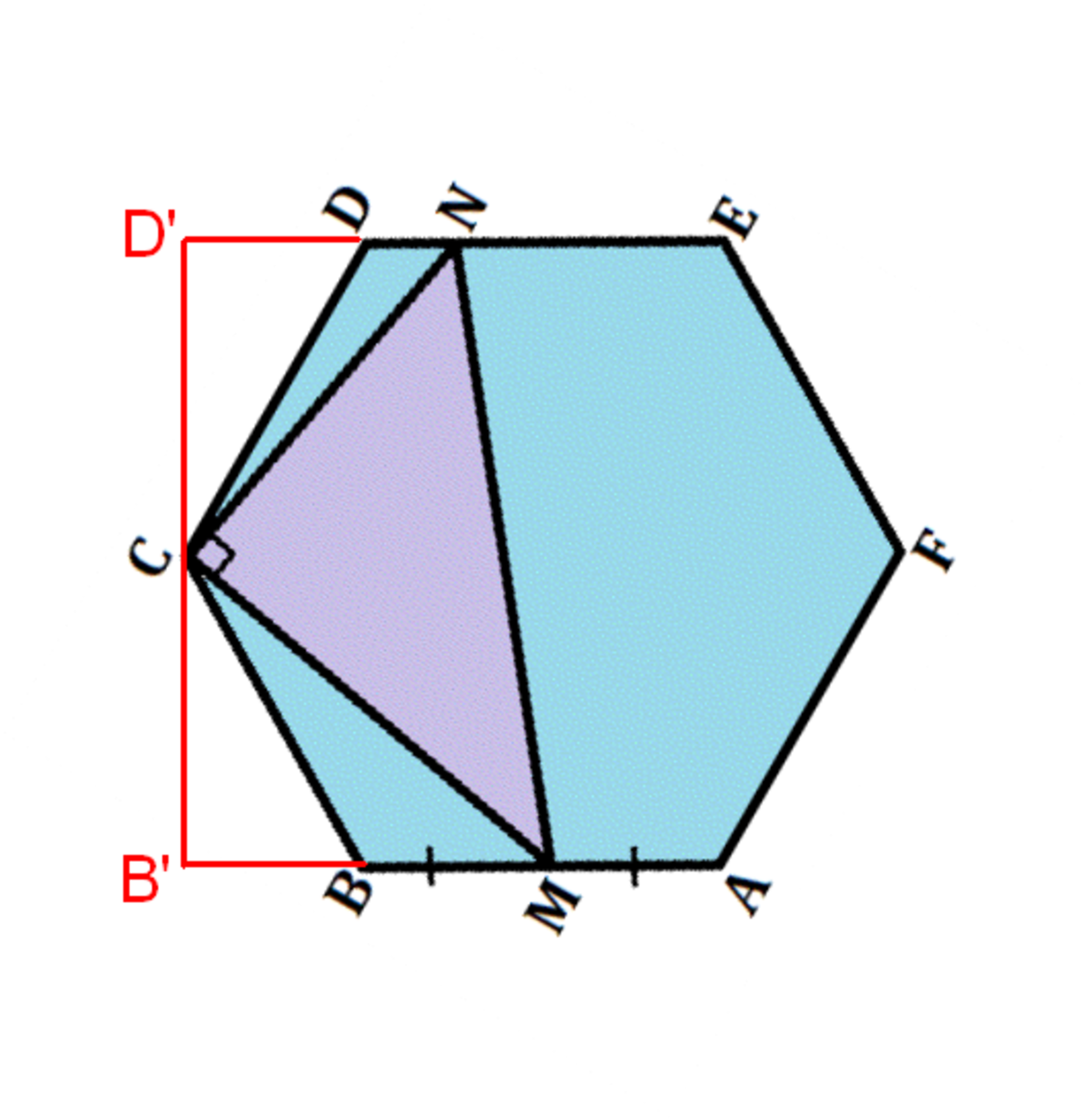
Point D ′ lies on the extension of line D E so that D D ′ C is a right-angle; point B ′ is defined similarly. D D ′ = B B ′ = 2 1 and B ′ C = C D ′ = 2 3 .
Since the triangles B ′ C M and D ′ C N are similar, B ′ C D ′ N = B ′ M C D ′
so B ′ M ⋅ D ′ N = B ′ C ⋅ C D ′ = 4 3 .
By Pythagoras... M N 2 = C M 2 + C N 2 = ( B ′ C 2 + B ′ M 2 ) + ( C D ′ 2 + D ′ N 2 ) = 2 3 + B ′ M 2 + D ′ N 2 = 2 B ′ M ⋅ D ′ N + B ′ M 2 + D ′ N 2 = ( B ′ M + D ′ N ) 2 = ( 1 + B M + D N ) 2
so M N = 1 + B M + D N = 1 + ( 1 − A M ) + ( 1 − E N ) = 3 − A M − E N .
Hence the perimeter of A M N E F is A M + M N + N E + E F + F A = A M + ( 3 − A M − N E ) + N E + 1 + 1 = 5
so the ratio is Perimeter 6-gon Perimeter 5-gon = 6 5
...which doesn't depend on the position of M along A B !
Nice solution! You'll be interested to know that there is also a non-trigonometric solution for this problem, can you find it?
Log in to reply
I am interested in that...and I've just noticed the ratio is independent of the position of M along A B ! Right, back to the drawing board...
I finally got it! I am going to update the solution once I am done eating.
Spoiler : It has to do with unit equilateral triangular lattice points.
Log in to reply
@David Vreken - was this the way you meant?
@Michael Huang - no time for eating! ;-) Although I think you might have done this yet another way...I hope I haven't just found a different ugly solution!
Log in to reply
@Chris Lewis – I have posted the solution.
@Chris Lewis – I love both your and @Michael Huang 's solutions, but I actually had a different method! I'll post it soon.
Alternative trig solution in a reply to this...
Log in to reply
Assume the hexagon has unit sides.
In triangle Δ M B C , M B = 2 1 , B C = 1 and ∠ M B C = 1 2 0 ∘ . By the cosine rule, we get M C 2 = M B 2 + B C 2 − 2 M B ⋅ B C ⋅ cos ∠ M B C = 4 7 so M C = 2 7 .
By the sine rule, M B sin ∠ M C B = M C sin ∠ M B C so sin ∠ M C B = 2 1 7 3 . We also get cos ∠ M C B = 2 7 5 .
Now, in triangle Δ C D N , C D = 1 , ∠ C D N = 1 2 0 ∘ and ∠ D C N = 1 2 0 ∘ − 9 0 ∘ − ∠ M C B = 3 0 ∘ − ∠ M C B . It follows that ∠ C N D = 3 0 ∘ + ∠ M C B .
Using the sine rule again, sin ∠ D C N D N D N = sin ∠ C N D C D = sin ( 3 0 + ∠ M C B ) sin ( 3 0 − ∠ M C B ) = 4 1 (where I've left out some trig expansion and substitution)
Also, using whatever rule we want now, we get C N = 4 2 1 .
By Pythagoras, M N = C N 2 + M C 2 = 4 7
Now we have everything we need; the perimeter of A B C D E F is 6 and the perimeter of A M N E F is A M + M N + N E + E F + F A = 2 1 + 4 7 + 4 3 + 1 + 1 = 5
so the ratio is Perimeter 6-gon Perimeter 5-gon = 6 5
Let each side of the regular hexagon be s , so that its perimeter is P A B C D E F = 6 s , and reflect △ M B C along M C and △ C D N along C N :
Since ∠ B C M + ∠ N C D = ∠ B C D − ∠ M C N = 1 2 0 ° − 9 0 ° = 3 0 ° , and ∠ B C M = ∠ B ′ C M and ∠ N C D = ∠ N C D ′ , then ∠ B ′ C M + ∠ N C D ′ = ∠ B C M + ∠ N C D = 3 0 ° , so ∠ B ′ C D ′ = ∠ M C N − ( ∠ B ′ C M + ∠ N C D ′ ) = 9 0 ° − 3 0 ° = 6 0 ° .
Since B C = B ′ C = C D = C D ′ = s , and since ∠ B ′ C D ′ = 6 0 ° , △ B ′ C D ′ is an equilateral triangle, which means B ′ D ′ = s .
Also, A M + M B ′ = A M + M B = s , and D ′ N + N E = D N + N E = s .
That means the perimeter of A M N E F is P A M N E F = ( A M + M B ′ ) + B ′ D ′ + ( D ′ N + N E ) + E F + A F = s + s + s + s + s = 5 s .
The ratio of the perimeters is then P A B C D E F P A M N E F = 6 s 5 s = 6 5 .
Therefore, a = 5 , b = 6 , and a + b = 1 1 .