Hey! What's that?
Let f be a double differentiable function and satisfy the condition f ( 0 ) = 0 , f ( 1 ) = 0 and d x 2 d 2 ( e − x f ( x ) − x 2 ) > 0 ∀ x ∈ ( 0 , 1 )
Then the sum of values of x ∈ ( 0 , 1 ) such that f ( x ) − 3 = ( x 2 − x ) e x is ϕ
The number of ordered pair(s) ( x , y ) of real numbers satisfying equation 1 + x 4 + 2 x 2 sin ( cos − 1 y ) = 0 is ζ .
Calculate ζ + ϕ .
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
upvote and like !!
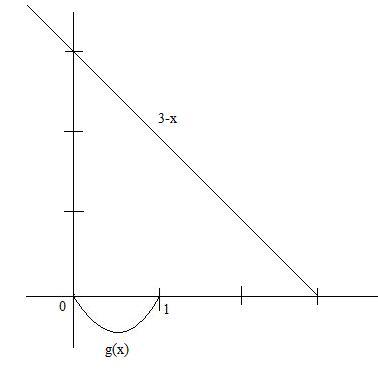
Lets take a function g(x)= e − x f ( x ) − x 2
Clearly from graph ϕ =0
Now sin ( c o s − 1 y ) = − 2 x 2 1 + x 4
from AM-GM sin ( c o s − 1 y ) ≤ -1
But sin ( c o s − 1 y ) ≥ 0
Hence ζ =0
what say @Kartik Sharma , @Pranjal Jain
Log in to reply
Yeah! Nicely done. But I must tell you that if this problem is given to me now(~10 months later), then I will also very probably try it the way you did(at least the 2nd sub-problem). Obviously, I will never use a graphical approach for some differential equation problem(probability of it being the correct approach is very less, I believe), though.
Log in to reply
Sometimes graphical method does help a lot. But yes, it requires being extremely carefull.
and you must try this
Nice problem! Little underrated!
1 As we know f(0) = 0, f(1) = 0. The function can be written as a multiple of x ( x − 1 )
We can also assume that the function is a multiple of an always positive multiple - e x . Hence, f ( x ) = e x x ( x − 1 ) ( x − c ) . Let us only assume that it is a 3rd degree polynomial at first.
e − x e x x ( x − 1 ) ( x − c ) − x 2 = x 3 − ( c + 2 ) x 2 + c x
d x 2 d 2 ( x 3 − ( c + 2 ) x 2 + c x ) = 6 x − 2 ( c + 2 )
6 x − 2 ( c + 2 ) > 0
Now, c can be − 3 , − 4 , − 5 . . . . .
f ( x ) = e x x ( x − 1 ) ( x + 3 + a ) for any non-negative integer a.
Now, we need to find the values of x such that
e x x ( x − 1 ) ( x + 2 + a ) = 3
But we know that in the interval ( 0 , 1 ) , it will be non-positive due to the term x − 1 ) . Therefore, there are no solutions.
2 1 + x 4 + 2 x 2 s i n ( c o s − 1 y ) = 0
Let c o s a = y ⇒ 1 − c o s 2 a = 1 − y 2 ⇒ s i n a = 1 − y 2
1 + x 4 + 2 x 2 1 − y 2 = 0
Let x 2 = b
b 2 + 2 b 1 − y 2 + 1 = 0
By quadratic formula,
b = 2 − 2 1 − y 2 ± 4 − 4 y 2 − 4
is complex until or unless y = 0 and 1 = ± 1
But then, for b = -1, x is complex and for b = 1, x = 1.
So, (1,0) can be a solution because 4 = ± 2
@Pranjal Jain
Log in to reply
- Are you sure 4 = ± 2 ?
- I think sin 2 a = 1 − y 2 ⇒ sin a = ± 1 − y 2
- I don't think you are supposed to "ASSUME" that f ( x ) is a 3 degree polynomial. You cannot even assume that it is a polynomial function.
- Try substituting (1,0) in the equation.
Log in to reply
That's a problem from AITS Full Test 3.
Log in to reply
@Ronak Agarwal – Yeah! I usually post question solving which gives me pleasure!
Hmm. Well, yes I get it. Thanks! BTW, can you post the solution of the 1st one?
I also tried solving differential equation. But I have no idea of a 2nd order differential.
Log in to reply
@Kartik Sharma – ( f ( x ) − 3 ) e − x = x 2 − x ⇒ e − x f ( x ) − x 2 = 3 e − x − x
You can try it now... Its almost done!
Log in to reply
@Pranjal Jain – Can you elaborate the solution more
Relevant wiki: Applying Differentiation Rules to Exponential Functions
Shamefully i spent approx. 30 mins.on the problem and 27 mins. figuring out what is f(x) and then i thought f(x) isn't really needed and the question was done :) now, since d x 2 d 2 ( e − x f ( x ) − x 2 ) > 0 ∀ x ∈ ( 0 , 1 ) now since differentials can be separated , we get to know that f(x) is a concave upwards and the graph of f(x)-3 will be shifted 3 units down , if l.h.s. is equated to r.h.s , then their graphs must intersect , now if we look at the function in r.h.s and differentiate it we will get the lowest value of it will be -0.14 something , and the max. value of f(x)-3 is -3 , the graph will not be close enough,let alone intersection . so , no of x satisfying it will be 0. now for the second part , the only way it is possible to have he equation satisfied is to have sin ( cos − 1 y ) = - 1 which is not possible , since the principal value branches of both function coincide only in first quadrant , and none of the function is -ve in first quadrant ! @Pranjal Jain i loved the problem that's why i wrote such a long solution :P