Hey! I have seen that before
2 , 6 , 1 2 , 2 0 , 3 0 , … , a n
Above shows the first few numbers of an increasing series. If the sum of these numbers equals 32430, find the value of the last term, a n .
The answer is 2070.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
Your work is very neat, I like that you incorporate colours into your work. Great job!
Bonus question: Instead of triangular numbers, we are given the sum of the first n smallest pentagonal numbers is 4200. Can you find the value of n ?
Challenge Master : Thank you! // The value of n is 20.
Log in to reply
Challenge Master: The value of n is 20, then!
Yeah! A good solution
How you do that Sir? The 2nd question is harder i thought.
Log in to reply
General sequence of pentagonal number is 1 , 5 , 1 2 , 2 2 , 3 5 , …
And general term of pentagonal number is p n = 2 3 n 2 − n
For sum of pentagonal number is,
1 + 5 + 1 2 + 2 2 + … + p n = 2 3 ( 1 2 ) − 1 + 2 3 ( 2 2 ) − 2 + 2 3 ( 3 2 ) − 3 + 2 3 ( 4 2 ) − 4 + … + 2 3 n 2 − n = i = 1 ∑ n ( 2 3 i 2 − i ) = 2 3 i = 1 ∑ n i 2 − 2 1 i = 1 ∑ n i = ( 2 3 ) ( 6 n ( n + 1 ) ( 2 n + 1 ) ) − ( 2 1 ) ( 2 n ( n + 1 ) ) = 4 2 n 3 + 3 n 2 + n − 4 n 2 + n = 2 n 3 + n 2 = n 3 + n 2 − 8 4 0 0 = ( n − 2 0 ) ( n 2 + 2 1 n + 4 2 0 ) = n = 4 2 0 0 4 2 0 0 4 2 0 0 4 2 0 0 4 2 0 0 4 2 0 0 4 2 0 0 0 0 2 0
Challenge Master: the value of n is 20
That's right the answer for this bonus question is 20. Good work @Krishna Ramesh , @Ikkyu San , @Kartik Sharma !
Yes, we will get n n (n+1) = 8400. This gives n = 20
An alternate method: Notice that a n + 3 − 3 a n + 2 + 3 a n + 1 − a n = 0 for any n . (The binomial coefficients here are not a coincidence! I think that the easiest way to prove it is to just bash the algebra, though...) Using this, we could sum this similarly to a geometric series: Call the sum S . Write down S , − 3 S , 3 S , and (S) in such a way to use the above identity, and... well, you'll see, I'm fairly certain it all works out in the end.
Log in to reply
On that identity: It's weird.
If a n is constant, then we have a n + 1 − a n = 0 .
If a n is linear, then we have a n + 2 − 2 a n + 1 + a n = 0 .
If a n is quadratic, then we have a n + 3 − 3 a n + 2 + 3 a n + 1 − a n = 0 .
If a n is cubic, then we have a n + 4 − 4 a n + 3 + 6 a n + 2 − 4 a n + 1 + a n = 0 .
Notice the similarities to the polynomials ( a − 1 ) 1 , ( a − 1 ) 2 , ( a − 1 ) 3 , … . The pattern continues, but I'm not sure I know the simplest way to prove this.
Log in to reply
Nice observation! Sketch out the pascal triangle, and you can see why.
Log in to reply
@Pi Han Goh – After writing that, I realized it could be proven easily by induction.
(I wonder if it works for fractional orders, similar to Newton's generalized binomial theorem?)
Log in to reply
@Akiva Weinberger – POST PROOF HERE! Fractional orders too? how?
Log in to reply
@Pi Han Goh – Wait, I don't know how to prove it for fractional orders (EDIT: "degrees"). I just wondered if it could be true.
For the induction thing, just notice that f ( n + 1 ) − f ( n ) brings the degree of f down one. Applying this transformation to a n repeatedly, we get the identities above.
Great solution.
2 + 6 + 1 2 + 2 0 + 3 0 + … + a n = 3 2 4 3 0 2 ( 1 + 3 + 6 + 1 0 + 1 5 + … + 2 a n ) = 3 2 4 3 0 Using the sum for triangular series formula, 2 ( 6 ( n ) ( n + 1 ) ( n + 2 ) ) = 3 2 4 3 0 ( n ) ( n + 1 ) ( n + 2 ) = 9 7 2 9 0 ⟹ n = 4 5 Since a n = n ( n + 1 ) a n = 4 5 ( 4 6 ) a n = 2 0 7 0
Moderator note:
Yes, a slight variation. To make this solution clearer, you could convert the triangular numbers in terms of binomial coefficients. Nevertheless, great work!
A Tetrahedral number is the sum of the first triangular numbers. One could easily obtain its identity by the hockey stick identity: ( 2 2 ) + ( 2 3 ) + ( 2 4 ) + … + ( 2 n + 1 ) = ( 3 n + 2 )
Just Ikkyu San method with little modification.
i
=
1
∑
n
(
i
2
+
i
)
=
6
n
(
n
+
1
)
(
2
n
+
1
)
+
2
n
(
n
+
1
)
=
2
n
(
n
+
1
)
∗
3
2
n
+
4
=
3
n
(
n
+
1
)
(
n
+
2
)
=
3
2
4
3
0
.
∴
3
(
n
+
1
)
3
≈
3
2
4
3
0
.
⟹
n
=
4
4
.
9
9
.
.
.
.
.
T
a
k
e
n
=
4
5
,
3
4
5
∗
4
6
∗
4
7
=
3
2
4
3
0
.
⟹
n
=
4
5
,
a
n
=
4
5
2
+
4
5
=
2
0
7
0
.
Moderator note:
Wow, a quick way to force out a solution. Nicely done! One should note that 3 n ( n + 1 ) ( n + 2 ) is an increasing function, so there's only one unique value when it's positive.
The sum of the sequence is : 2 + 6 + 1 2 + . . . . = 2 ( 1 + ( 1 + 2 ) + ( 1 + 2 + 3 ) + . . . . + ( 1 + 2 + . . . n ) )
The problem is : how much is 2 S Let's find S S = ( 1 + ( 1 + 2 ) + ( 1 + 2 + 3 ) + . . . . . . + ( 1 + 2 + . . . . n ) )
Let' draw a picture!
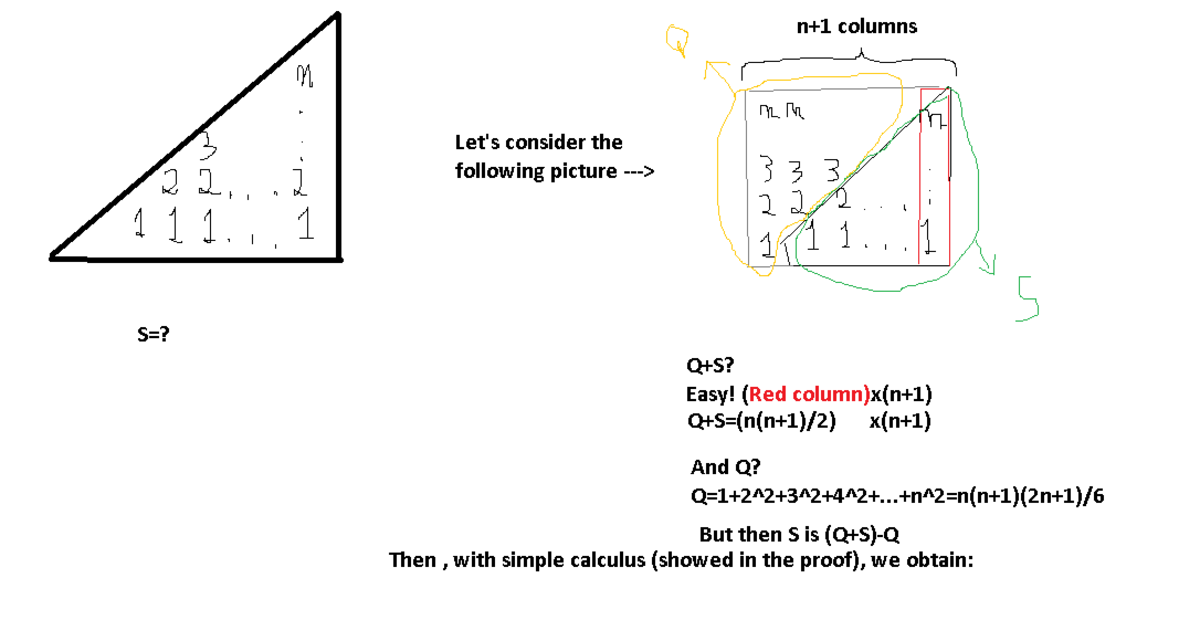
Q + S = 2 n ( n + 1 ) 2 Q = 1 2 + 2 2 + 3 2 + . . . + n 2 = 6 n ( n + 1 ) ( 2 n + 1 ) And so S = ( Q + S ) − Q = 2 n ( n + 1 ) 2 − 6 n ( n + 1 ) ( 2 n + 1 ) = 6 n ( n + 1 ) ( n + 2 )
From this , we obtain 2 S = 3 n ( n + 1 ) ( n + 2 ) = 3 2 3 4 0 Notice that n ( n + 1 ) ( n + 2 ) ∼ n 3 . 3 3 2 3 4 0 ∗ 3 ∼ 4 5 . We try n = 4 4 and it works
Then a n = n ( n + 1 ) = 2 0 7 0
For me, it's easier to see a pattern with recursive loops, so using a bit of python to help me. Although, it is much easier to do Ikkyu's method if you notice the pattern.
1 2 3 4 5 6 7 8 9 |
|

2 + 6 + 1 2 + 2 0 + … + a n = ( 1 2 + 1 ) + ( 2 2 + 2 ) + ( 3 2 + 3 ) + ( 4 2 + 4 ) + … + ( n 2 + n ) = i = 1 ∑ n ( i 2 + i ) = i = 1 ∑ n i 2 + i = 1 ∑ n i = 6 n ( n + 1 ) ( 2 n + 1 ) + 2 n ( n + 1 ) = 6 2 n 3 + 3 n 2 + n + 3 n 2 + 3 n = 3 n 3 + 3 n 2 + 2 n = n 3 + 3 n 2 + 2 n − 9 7 2 9 0 = ( n − 4 5 ) ( n 2 + 4 8 n + 2 1 6 2 ) = n = 3 2 4 3 0 3 2 4 3 0 3 2 4 3 0 3 2 4 3 0 3 2 4 3 0 3 2 4 3 0 3 2 4 3 0 0 0 4 5
From sequence 2 , 6 , 1 2 , 2 0 , 3 0 , . . . → 1 2 + 1 , 2 2 + 2 , 3 2 + 3 , 4 2 + 4 , 5 2 + 5 , . . .
Therefore, a n = n 2 + n → a 4 5 = 4 5 2 + 4 5 = 2 0 2 5 + 4 5 = 2 0 7 0