High Fives!

Calculus Level 4

$\Large \prod_{n=1}^{\infty}\dfrac{(1+\frac{1}{n})^5}{1+\frac{5}{n}} = \, ?$

The answer is 120.

5 solutions

Brian Charlesworth
Jan 12, 2016

The infinite product definition of the gamma function is $\displaystyle\Gamma(z) = \dfrac{1}{z} \prod_{n=1}^{\infty}\dfrac{(1 + \frac{1}{n})^{z}}{1 + \frac{z}{n}}$ .

Thus the given expression is $5 * \Gamma(5) = 5*4! = \boxed{120}.$

@Otto Bretscher , @Brian Charlesworth Can you tell me how to improve my Calculus and I want to start from very basic to very high level?

Department 8 - 5 years, 5 months ago

I used to ask the same question to myself few months back...

In calculus you need some knowledge! I can suggest a youtube channel for gamma + zeta function.You can set the digamma in the brilliant wikis!

zeta function

gamma function

Laplace transform

other basics can be learnt at khanacademy

Hope this helps!

Aareyan Manzoor - 5 years, 5 months ago

Well thanks it helps a lot!

Department 8 - 5 years, 5 months ago

I would first study a solid introduction to the calculus, like Courant's "Differential and Integral Calculus" (I learned from this one), Hardy's "A Course of Pure Mathematics", or Spivak's "Calculus". Some of the modern American calculus texts are too dumbed down to be useful or interesting to the intellectually curious reader.

Otto Bretscher - 5 years, 5 months ago

Thank you sir

Department 8 - 5 years, 5 months ago

@Department 8 – Let us know how it goes! Enjoy!

I have often seen students, even here on Brilliant, who may know some fun facts about some obscure functions, but who lack an understanding of the basics and the "big picture" of calculus. It's important to study the basics first, in a solid way!

Otto Bretscher - 5 years, 5 months ago

@Otto Bretscher – Yeah I am one of the students.

Department 8 - 5 years, 5 months ago

@Otto Bretscher – Sir you may try this problem.

Department 8 - 5 years, 5 months ago

Yes, this is the right approach for those who know the properties of the gamma function! (+1)

Otto Bretscher - 5 years, 5 months ago

Adrian Castro
Jan 12, 2016

$\prod_{n=1}^{\infty}\frac{(1+\frac{1}{n})^5}{1+\frac{5}{n}}=\prod_{n=1}^{\infty}\frac{(\frac{n+1}{n})^5}{\frac{n+5}{n}}=\prod_{n=1}^{\infty}\frac{(n+1)^5}{n^4\cdot(n+5)}=\frac{2^5}{1^4\cdot6}\cdot\frac{3^5}{2^4\cdot7}\cdot\frac{4^5}{3^4\cdot8}\cdot\frac{5^5}{4^4\cdot9}\cdot\frac{6^5}{5^4\cdot10}\cdot\cdot\cdot$ Let $a_{n}=\frac{(n+1)^5}{n^4\cdot(n+5)}$ note that $\lim_{n\rightarrow\infty}a_n=1$ $\therefore\prod_{n=1}^{\infty}a_n=\frac{2^5}{1^4\cdot6}\cdot\frac{3^5}{2^4\cdot7}\cdot\frac{4^5}{3^4\cdot8}\cdot\frac{5^5}{4^4\cdot9}\cdot\frac{6^5}{5^4\cdot10}\cdot\frac{7^5}{6^4\cdot11}\cdot\frac{8^5}{7^4\cdot12}\cdot\cdot\cdot 1=1\cdot2\cdot3\cdot4\cdot5=\boxed{5!}$

Perhaps the best thing to do with this solution method is to evaluate the partial product, so $\begin{array}{rcl} \prod_{n=1}^N \big(1 + \tfrac{1}{n}\big)^5 & = & \prod_{n=1}^N \frac{(n+1)^5}{n^5} \; = \; \left(\frac{(N+1)!}{N !}\right)^5 \; = \; (N+1)^5 \\ \prod_{n=1}^N \big(1 + \tfrac{5}{n}\big) & = & \prod_{n=1}^N \frac{n+5}{n} \; = \; \frac{(N+5)!}{5! N!} \end{array}$ so that $\begin{array}{rcl} \displaystyle\prod_{n=1}^N \frac{\big(1 + \frac{1}{n}\big)^5}{1 + \frac{5}{n}} & = & \displaystyle\frac{5! N! (N+1)^5}{(N+5)!} \; = \; \frac{120 (N+1)^5}{(N+1)(N+2)(N+3)(N+4)(N+5)} \\ & = & \displaystyle\frac{120(N+1)^4}{(N+2)(N+3)(N+4)(N+5)} \end{array}$ so that the limit $\prod_{n=1}^\infty \frac{\big(1 + \frac{1}{n}\big)^5}{1 + \frac{5}{n}} \; = \; \lim_{N\to\infty} \frac{120 (N+1)^4}{(N+2)(N+3)(N+4)(N+5)} \; = \; 120$ is obvious.

Infinite products are a little cranky; the fact that $\lim_{n\to\infty} a_n = 1$ is not enough to ensure that the infinite product $\prod_{n=1}^\infty a_n$ exists, as your last line seem to imply. Consider the difference between $a_n = 1 + \tfrac{1}{n}$ and $a_n = 1 + \tfrac{1}{n^2}$ , for example; the first product diverges, but the second converges

Mark Hennings - 5 years, 5 months ago

True, it's not formally rigorous but in my solution I would think it sufficed to show intuitively first that the term a_n does not approach zero therefore knowledge of how the first few terms cancel out combined with this fact essentially tells us how all the terms would behave logically. In other words, we know the /(n-1/)th term and the limit tells us the nth term to infinity necessary to complete the logic of the solution. However, I completely see your point and in fact find your solution very interesting.

Adrian Castro - 5 years, 5 months ago

There is always a risk inherent in just showing what happens for the first few terms. Ask yourself: "what are the next two terms in the sequence $1,2,4,8,\ldots$ ?" Then check on Conway's Soldiers to see why " $20,\infty$ " is an unexpected answer!

Mark Hennings - 5 years, 5 months ago

I think that Adrian's solution (the last line of work) nicely illustrates what you are doing more formally, Dr. Hennings. Adrian finds the partial product $\frac{5!\times 8^4}{9*10*11*12}$ , or, more generally, $\frac{5!\times (n+1)^4}{(n+2)(n+3)(n+4)(n+5)}$ , with a limit of 5!.

I had asked Adrian to add a few more terms to show this pattern more clearly. By my informal standards, this will suffice.

Otto Bretscher - 5 years, 5 months ago

Adrian's proof is, in essence, the same as mine. What I was pointing out to him was the need for precision in analysis. The finite product argument identities exactly the same pattern as Adrian did, but is absolutely clear about what happens in the limit.

I am, perhaps, being pedantic, but there is a good place for care begin taken in analysis. Seeing terms cancel in a pattern only gets you so far. The argument $\prod_{n=1}^\infty \big(1 + \tfrac{1}{n}\big) \; =\; \prod_{n=1}^\infty \tfrac{n+1}{n} \; = \; \frac{2}{1} \times \frac{3}{2} \times \frac{4}{3} \times \frac{5}{4} \times \cdots \; = \; 1$ is clearly faulty, but it follows from saying that every integer in a numerator cancels with the denominator of the following fraction, so that only the initial $1$ in the first denominator remains uncancelled. This on the face of it plausible argument is only scotched by showing that the product of the first $n$ terms is $n+1$ , with one large uncancelled term in the numerator! (Absolutely convergent) infinite series are fairly robust, in that they can be manipulated, rearranged, and so on with a fair degree of impunity; this is not the case with infinite products.

My main objection was the statement that $\lim_{n\to\infty}a_n=1$ implied the convergence of the infinite product. To be sure of the infinite product being convergent, we can either:

observe that $a_n-1 = O(n^{-2})$ as $n\to\infty$ , so that $\sum_n |a_n-1| \,<\, \infty$ ; this guarantees that the infinite product converges,
rely on the Gamma function formula, trusting that someone else has done the convergence analysis,
calculate the finite product, as I did.

I know which solution I think is nicer!

Mark Hennings - 5 years, 5 months ago

@Mark Hennings – If I had not been too lazy to write a solution myself, I would have written Adrian's first line, with two more terms in the product, and then said: We can see that the partial product, which is , $\frac{5!\times (n+1)^4}{(n+2)(n+3)(n+4)(n+5)}$ , tends to $\boxed{5!}$ . While this argument is informal, it is rigorous.

As you may have noticed, I hate to write solutions that involve more than two lines, and I find that is rarely necessary to make them longer on Brilliant ;)

Otto Bretscher - 5 years, 5 months ago

@Otto Bretscher – That would have been fine! You would have evaluated the partial product. I would be quite happy (since the pattern is pretty obvious) to leave the confirmation of the value of the partial product to the interested reader; the proof should state it.

Mark Hennings - 5 years, 5 months ago

Yes, very nicely explained "from first principles". I would write one or two more factors in the last row. $\frac{7^5}{6^4 \times 11} \frac{8^5}{7^4 \times 12}$ , so that people can really see how things cancel out from 6 on up.

Otto Bretscher - 5 years, 5 months ago

Thank you Otto! And yes, you're right about the last row, I'll add it right now.

Adrian Castro - 5 years, 5 months ago

Very nice solution!

Ramón Martins - 5 years, 5 months ago

Thanks man.

Adrian Castro - 5 years, 5 months ago

Akshay Sharma
Jan 13, 2016

Here is the solution: 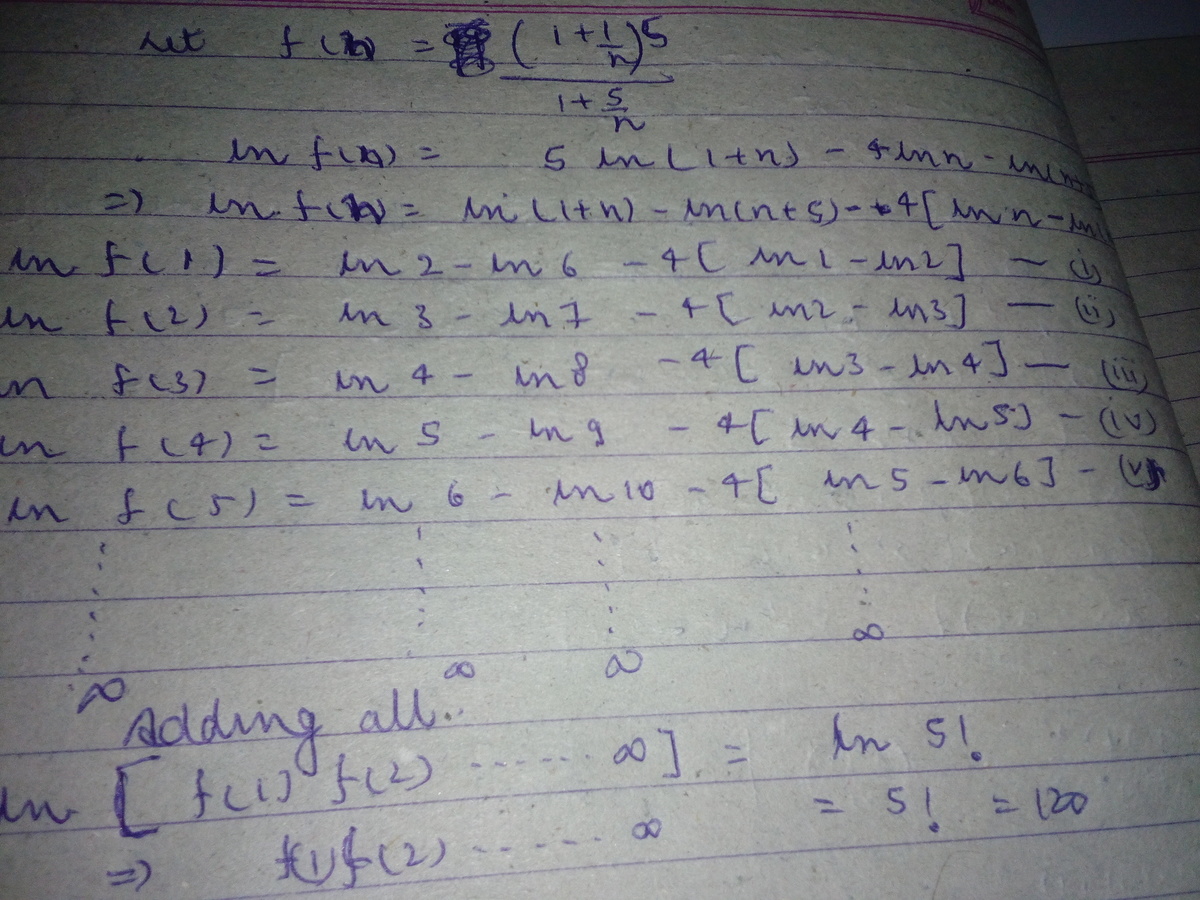Actually I don't know how to use LaTex. So I prefer to write solution this way.

Ramiel To-ong
Jan 20, 2016

i love this one.

Maharnab Mitra
Jan 18, 2016

$\prod_{n=1}^{\infty}\frac{(1+\frac{1}{n})^5}{(1+\frac{5}{n})}=\frac{\prod_{n=1}^{\infty}(1+\frac{1}{n})^5}{\prod_{n=1}^{\infty}(1+\frac{5}{n})}=\frac{(\prod_{n=1}^{\infty}(1+\frac{1}{n}))^5}{\prod_{n=1}^{\infty}(1+\frac{5}{n})}$

Let's look at the numerator first.

$\prod_{n=1}^{\infty}(1+\frac{1}{n})=(1+\frac{1}{1})(1+\frac{1}{2})(1+\frac{1}{3})(1+\frac{1}{4})....$ $=(2)(\frac{3}{2})(\frac{4}{3})(\frac{5}{4})....$ $=1$

Now the denominator.

$\prod_{n=1}^{\infty}(1+\frac{5}{n})=\prod_{n=1}^{\infty}(\frac{n+5}{n})=\frac{\prod_{n=1}^{\infty}(n+5)}{\prod_{n=1}^{\infty}(n)}=\frac{6\times 7\times 8\times 9\times ....}{1\times 2\times 3\times 4\times ....}=\frac{1}{5!}$

So, $\frac{1^5}{\frac{1}{5!}}=5!=120$

High Fives!

The answer is 120.

5 solutions

0 pending reports