Hit for the cycle
Suppose A B C D is a cyclic quadrilateral with side A D being a diameter of length d , sides A B and B C both having length a and side C D having length b such that a , b , d are all positive integers with a = b .
Determine the minimum possible perimeter of A B C D .
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I made this wrong -_- don't know why but I got a 2 = b d anyways this goes to my favorites :D
Log in to reply
I'm glad you liked it. I was thinking of inscribing a circle in ABCD as the last step, but I figured that would be excessive. :)
Log in to reply
I m getting 1.5288... For inradius is it correct?
Log in to reply
@Krishna Sharma – This is interesting. Not every quadrilateral has an incircle, (i.e., an inscribed circle tangent to all four sides). A necessary and sufficient condition for a quadrilateral to be "tangential", i.e., have an incircle tangent to all four sides, is that the pairwise sums of opposite side lengths are equal. But in this case we have 8 + 2 = 7 + 2 , so our quadrilateral is not tangential and hence cannot have an incircle or inradius. I did a calculation as if it were tangential and got a value of 1 9 8 1 4 = 1 . 5 7 5 . . . . So judging from your value of 1 . 5 2 8 8 . . . it would appear that you know all this and calculated the radius of the largest circle which can be inscribed in ABCD, a circle which in fact is only tangent to three of the sides. Is this assumption correct?
So now we have to take the sides in sets of three and determine the largest circle that is tangent to each of those sides, (only certain sets will yield a fully inscribed circle, though). I did this with the sides length 7, 8 and 2, where the side length 2 was adjacent to the side length 7, and found a radius of 1 . 5 0 6 . . . . . We could also look at the set involving side lengths 2,2,7; is this the one you found your value of 1.5288.... for?
This has all the makings for a good question to post. :)
Log in to reply
@Brian Charlesworth – Wow! I never realised this much could have been done with incircle...I forgot pitot's theorem -_- I didn't assumed anything(such a noob) and just used the formula r = S Δ , Now I m thinking that is this value 1.5288.... Is correct or not? Since the formula was specified for incircle and no incircle can be inscribed I think this value could be incorrect.
How you calculated the values like 1.506...? Is there any formula or way to do this? If yes then please share it.
I m sure that you know this
Δ c y c l i c q u a d = ( S − a ) ( S − b ) ( S − c ) ( S − d )
Where S = 2 a + b + c + d
Where you got 1 9 8 1 4 have you used the above formula? If yes then it comes out to be 3 8 1 5 1 5 = 1 . 5 2 8 8 . . .
Log in to reply
@Krishna Sharma – Oh, right, Brahmagupta's formula; I remember now learning that one from you some time ago. For some reason I forgot and ended up using Bretschneider's formula and must have made a mistake in my calculation. So yes, if ABCD had been tangential than the inradius would have been 1 . 5 2 8 8 . . . . .
What I did to get the 1 . 5 0 6 . . . . value was extend the sides of B C and A D so that they would meet at a point P , thus creating Δ P C D for which I then calculated the inradius in the usual way. I'm pretty sure this will be the largest possible radius for an inscribed circle, but there is one other possibility that is proving harder to make a calculation for.
Really Tough... and cool problem as always ! Thanks Sir ..I couldn't solve it .. but understand after your solution !
I missed to prove that with d = 8 we indeed get the least perimeter. If a higher value of d would have yielded a lesser perimeter, I would have certainly banged my head for an extra hour...
Simple yet tricky problem...
Very nice problem. It took me two tries to solve it because I wasn't thinking on my first try. I used this formula on integral square roots.
Luckily, I found the generalized case for all quads of this type with two sides equal and one as the diameter. I'll post my own problem on this leave it up to you to solve it :3.
Btw, I began the problem the EXACT same way as you lol.
Log in to reply
Haha. Your problem took me two tries because I can't add, apparently. :)
Log in to reply
Haha, I have that trouble too. I'm curious as to how you did it (I'll have my solution up in a few hours).
Btw, hope you don't mind the picture I added. You can remove it if you prefer not to have it.
A little use of ptolemy's theorem and componendo-dividendo also gives the result.
Oh so you did it like this! Nice! Mine was not as good as yours. I took the value of d from the quadratic formula and then did some bashing. Yeah this one is better! But still I think it's actually overrated.
Log in to reply
Brian Sir doesn't decide points..... it was decided by staff according to write or wrong number of attempts ... Brian sir can just put it as Level-5 which is off-course deserve by this question....So i don't think that it is overrated ....!
Log in to reply
I know that! It maybe that it is not overrated but that would be just perspective. It's just of ~350 points because of the solved %.
Its not at all overratted ! -_-
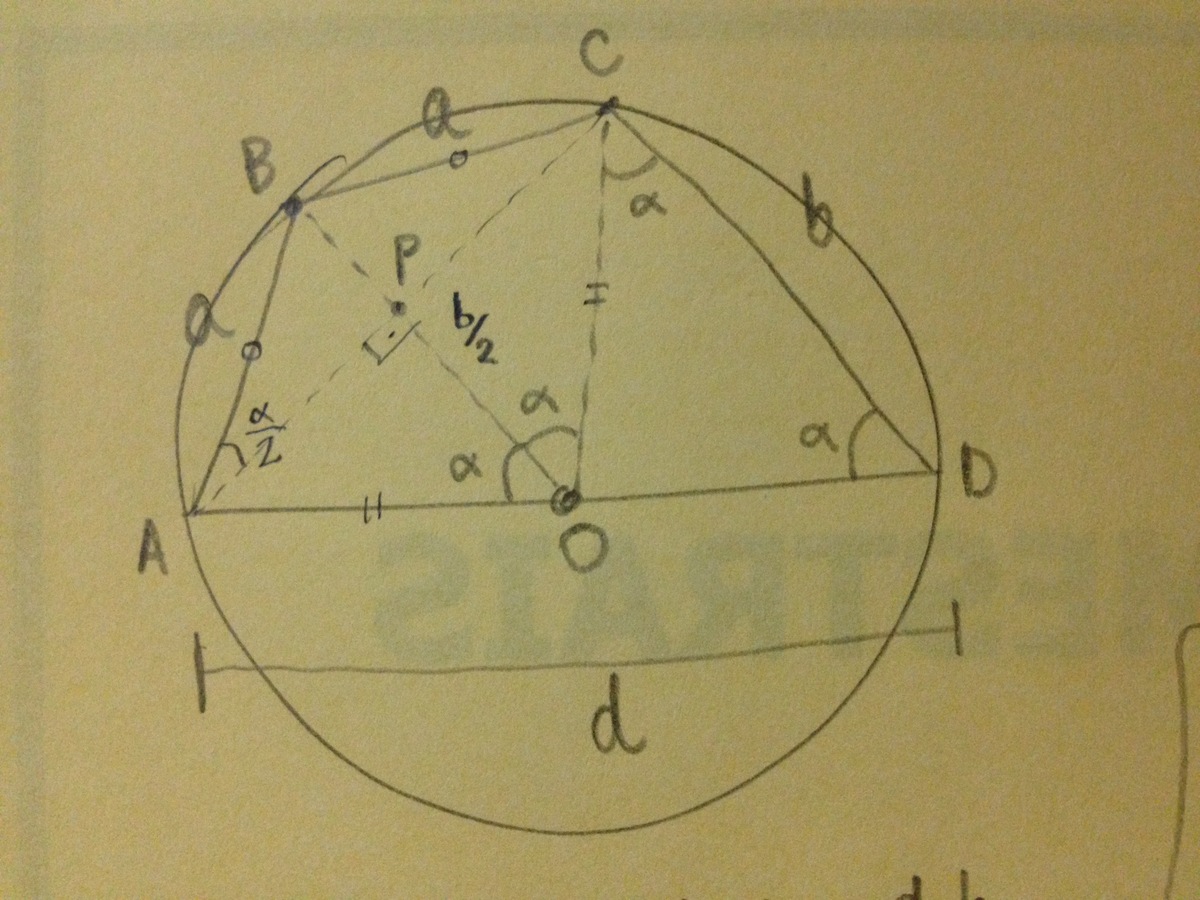
∠ A O B = ∠ B O C = ∠ O D C because central and inscribed angles.
∠ O C D = ∠ O D C because △ C O D is isosceles. So, B O is parallel to C D . O is midpoint of A D , so O P = 2 b (please refer to draw above)
B O = A O = D O = 2 d . Then, B P = B O − P O = 2 d − b
△ B A P is right because ABCO is a kite and its diagonals are perpendicular. It gives us s i n ( 2 α ) = 2 a d − b
△ A C D is right too and gives us c o s ( α ) = d b
Now is time to remember this trigonometric formulae for double angles: c o s ( α ) = 1 − 2 s i n 2 ( 2 α )
Using it, we have: d b = 1 − 2 ( 2 a d − b ) 2 . Doing easy math, we get d ( d − b ) = 2 a 2 .
As a, b, d are integer and (a + a + b + d) the minimum possible, I started with a = 1, then d ( d − b ) = 2 → d = 2 and b = 1 but we cannot have a = b.
Next try was a = 2 and then d ( d − b ) = 8 → d = 8 and b = 7 .
Others tries show me larger perimeters, so the minimum one is 2 + 2 + 7 + 8 = 1 9 .
Congratulations for the beautiful problem. Was very nice to solve it.
Great solution. I'm glad you enjoyed working on the problem. :)
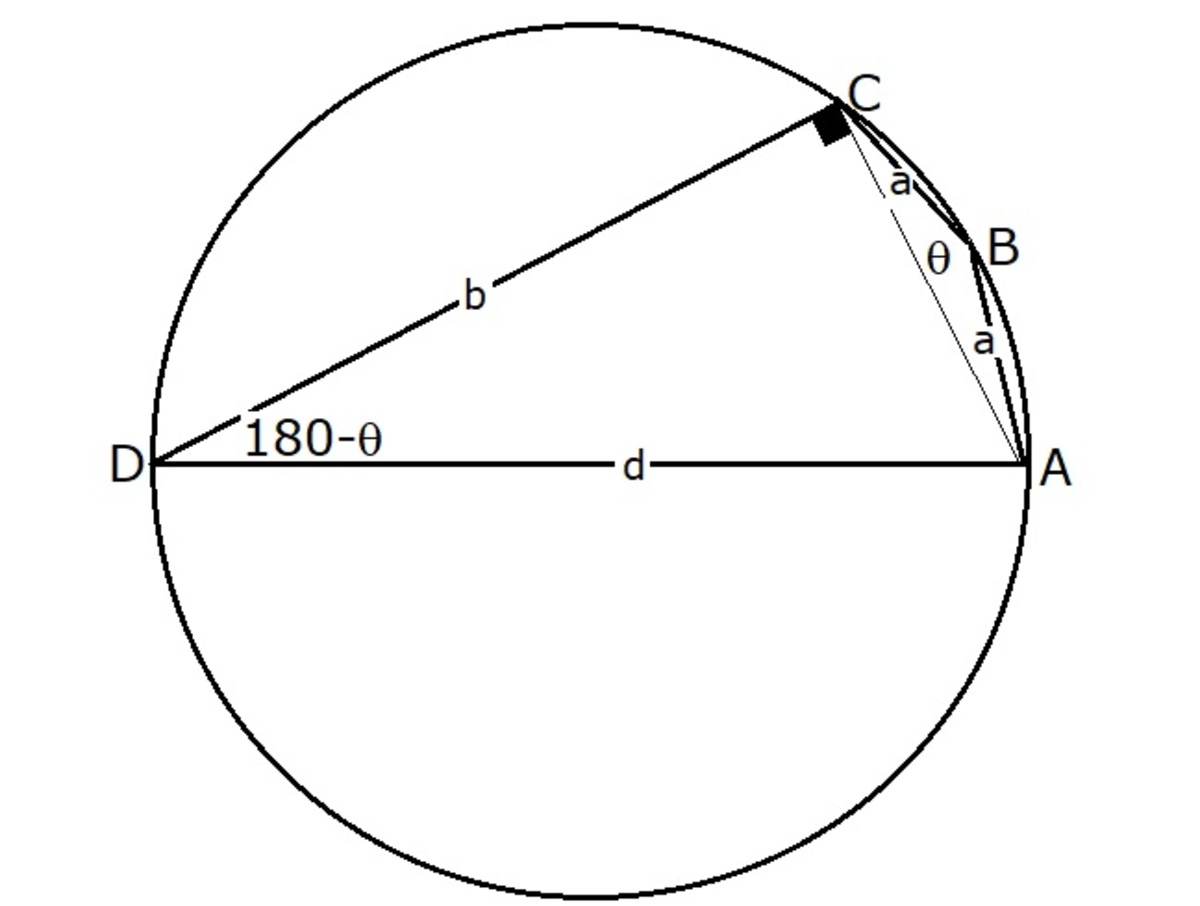
Let ∠ A B C = θ . Then since A B C D is cyclic we have that ∠ C D A = 1 8 0 ∘ − θ . Also, since A D is a diameter we have that ∠ A C D = 9 0 ∘ .
Using the Cosine rule on Δ A B C we see that ∣ A C ∣ 2 = 2 a 2 ( 1 − cos ( θ ) ) .
Next, as Δ A C D is right-angled at C we have that ∣ A C ∣ 2 = d 2 − b 2 and that
cos ( ∠ C D A ) = d b ⟹ cos ( θ ) = − d b .
Combining these results, we see that
d 2 − b 2 = 2 a 2 ( 1 + d b ) ⟹ d ( d 2 − b 2 ) = 2 a 2 ( d + b ) ⟹ 2 a 2 = d ( d − b ) , (i).
Now clearly d > b , so we cannot have d = 1 . So look at d = 2 . Plug this into (i) to get 2 a 2 = 2 ( 2 − b ) ⟹ b + a 2 = 2 . Since a , b must be positive integers we would require that a = b = 1 , but as it was specified that a = b we cannot have d = 2 .
Now look at the case where d ≥ 3 is prime. Looking at equation (i), we see that since d ≥ 3 cannot divide 2 it must divide a 2 . But since d is prime it must then divide a . But since it is clear that d > a we cannot have that d ∣ a , and thus d cannot be a prime.
So now look at the cases where d is a composite number, starting with 4 , 6 , 8 , 9 , . . . . .
With d = 4 equation (i) becomes a 2 = 2 ( 4 − b ) . For b = 1 or b = 3 we have, respectively, a 2 = 6 or a 2 = 2 , making a non-integral. With b = 2 we end up with a = 2 , violating the condition a = b .
With d = 6 equation (i) becomes a 2 = 3 ( 6 − b ) . Trying values for b of 1 , 2 , 4 , 5 yield non-integral values for a , and trying b = 3 yields a = 3 . Thus d cannot be 6 .
With d = 8 equation (i) becomes a 2 = 4 ( 8 − b ) . Trying b = 7 gives a = 2 , thus giving us a valid solution with A B C D having a perimeter of 2 + 2 + 7 + 8 = 1 9 . No other value of b yields an integral value of a .
Now with d = 9 we can go through the cases for each value for b to find that b = 1 , a = 6 and b = 7 , a = 3 are valid solutions. But these solutions each yield a perimeter of 2 2 , , so 1 9 is still our minimum.
With d > 9 and composite, clearly ( 2 a + b ) > 9 as well, forcing any possible perimeters we find for such values for d to exceed 2 0 . Thus we can conclude that the minimum possible perimeter is 1 9 .