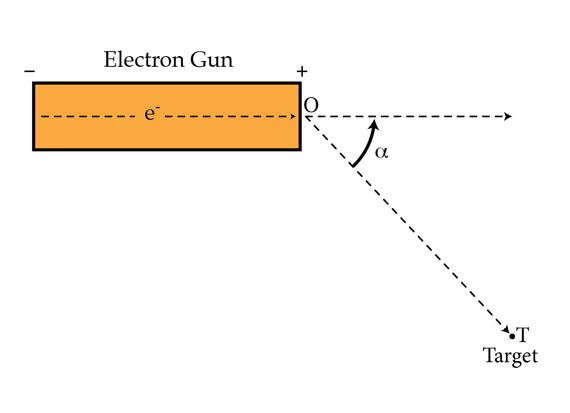
Hitting the target in two different ways

When the magnetic field is into the page the electrons describe a segment of a circular path, call it P1. Let $v$ be the speed of the electrons. The radius of the orbit is obtained from $qvB=m \frac{ v^{2}}{R} \Rightarrow R=\frac{mv}{q B}$ If $d$ is the distance from point O to point T, then simple trigonometry yields $\sin(\alpha) =\frac{d}{2 R}.$ Theferore, the magnitude of the magnetic field equals $B=2 \sin(\alpha) \frac{mv}{q d} .$ When the magnetic field is directed along the line $\overline{OT}$ the motion of the particles is more complex. In this case, their motion can be decomposed into circular motion and constant velocity motion. As a consequence, the electrons move in a helical path. The radius of the helix is in this case is $r=\frac{m v_{\perp}}{q B}.$ where $v_{\perp}= v \sin(\alpha)$ . The period, however, is independent of $\alpha$ . $T= \frac{2 \pi r}{v_{\perp}}=\frac{2 \pi m}{q B}$ The motion along the z-axis is given by the equation $z(t)= v_{\parallel} t= v \cos(\alpha)t$ Thus the time it takes for the electrons to reach the coordinate $z=d$ is $\tau=\frac{d}{v \cos(\alpha)}$ . The electrons hit the target if $\tau= n T$ with $n=1,2 \ldots$ . From the above equations we find that the possible values of the magnetic field are $B_{n}=2 \pi n \cos(\alpha) \frac{mv}{q d}$ Since the magnitude of the magnetic field is fixed we arrive at the relation $\tan(\alpha)= n \pi \rightarrow \alpha_{min}= \tan^{-1}(\pi)= 72.3^{\circ}.$

Let the charge of each electron be $q$ , the velocity be $v$ , the mass be $m$ , and the radius of the circular path be $r$ . The forces acting on the electrons are:

i) The inward Lorentz force with magnitude $qvB$
ii) The outward centrifugal force with magnitude $\frac{mv^2}{r}$

Since the net force acting on each electron is zero, we must have: $qvB= \frac{mv^2}{r} \implies B= \frac{mv}{qr}$ Let the length of the line segment $OT$ be $d$ . Note that $\sin \alpha = \frac{d}{2r} \implies r= \frac{ \sin \alpha }{2d}$ Plugging this value in the first equation, we obtain: $B= 2 \sin \alpha \frac{mv}{qd}$

When the magnetic field is directed along the line $OT$ , the electrons will describe a spring-like path $P_2$ as in the figure below:

Here's the link in case the image doesn't load: http://s23.postimg.org/6wjzd79h7/pic1.png

Let the radius of each small circle be $r_2$ . The forces acting on each electron are:

i) Inward Lorentz force with magnitude $q v_{\perp } B = q v B \sin \alpha$ where $v_{\perp}$ is the component of velocity perpendicular to the magnetic field
ii) Outward centrifugal force with magnitude $\frac{mv^2}{r_2}$

Balancing the forces, we obtain: $q v B \sin \alpha = \frac{mv^2}{r_2} \implies r_2= \frac{mv \sin \alpha }{qB}$ The time period of one revolution about a small circle will be: $T= \frac{2 \pi r_2}{v \sin \alpha}$ Substituting the expression for $r_2$ , we obtain:
$T= \frac{2 \pi m}{qB}$ We take the $z$ axis to be the line $OT$ . At time $t$ , the distance from an electron to the $O$ along the $z$ axis will be: $z(t)= v t \cos \alpha$ The time taken for the electrons to reach the point $T$ will be $t= \frac{OT}{v \cos \alpha } = \frac{d}{v \cos \alpha }$ . The electrons will pass through point $T$ iff $t$ is an integral multiple of $T$ (the time taken to orbit through the smaller circles). Let $t= nT$ , where $n \in \mathbb{N}$ . Plugging this value in the above equation, we obtain: $B= 2 \pi n \cos \alpha \frac{mv}{qd}$ Note that the magnetic field remains constant. Substituting values from the previous equations, we can show that $\alpha = \tan^{-1} (n \pi )$ Since we want to minimize $\alpha$ , we set $n=1$ , which gives $\alpha = \tan^{-1} \pi \approx 72.3^{\circ }$ .

B directed into the page: The electron enters the magnetic field region with its initial velocity being prependicular to the field's direction.So it will move on a circle (K,R) which means that: Fcentripental=Florentz or mu^2/R=Bqu or R=mu/Bq(1) By the problem's geometry we get that: (OT)=2 R sina which due to (1) is (OT)=2 m usina/Bq (2) B directed along the line OT: In this case the angle between the magnetic field and the electron's initial velocity is equal to a.So it will do two motions at the same time, one circular due to u'=usina, and one linear with constant speed u''=ucosa. Circular motion: The same way we got (1) we find that: R'=mu'/Bq and since u'=2 pi R'/T we get u'=2 pi m u'/B q T or T=2 pi m /B q. Linear motion: (OT)=u'' t or t=(OT)/u'' where t is the total time that taked the electron to move from O to T.Because of (2) we get: t=2 m u sina/B q u cosa=2 m tana/B q. In order for the electron to hit the target,when time t has past,it must have completed N full circles with N greater or equal to 1.So we coclude that: t=N T or 2 m tana/B q=2 pi m /B q or tana=N pi.By the last equation we get (tana)min=(N pi)min or tan(amin)=Nmin pi and since N is greater or equal to 1 it's Nmin=1.Thus tan(amin)=pi=3.14.Using a calculator we get that amin=72.3 degrees .

For the first case when $B$ points downwards, the magnitude of force experienced by the electron is $F=evB$ which is equal to the centripetal force $\frac{mv^2}{R}$ as it follows a circular path.

[ $e$ =charge of electron, $v$ =velocity of electron]

So, $evB= \frac{mv^2}{R} \implies R= \frac{mv}{eB}$ which is the radius of the circular path. Now, from the figure, the displacement of the electron $AT=2Rsin \alpha = \frac{2mvsin \alpha}{eB}$ .

Image

For the second case, the velocity of electron can be resolved into two components (as shown in the figure) such that one is along the magnetic field and the other is perpendicular to it.

Image

$vcos \alpha$ is responsible for the displacement and $vsin \alpha$ is responsible for its circular path. As it covers a full circle due to $vsin \alpha$ , $vcos \alpha$ makes it reach the target T at the same time. Time period of the electron is given by $\frac{2 \pi m}{eB}$ .

Now, we apply $\frac{Displacement}{speed} =time$

$\implies \frac{\frac{2mvsin \alpha}{eB}}{ vcos \alpha} = \frac{2mv}{eBv} tan\alpha =\frac{2 \pi m}{eB}$ which is the time period. This gives $tan \alpha = \pi \implies \alpha =72.3^o$

Here is a sketch of the solution.

Consider the motion of electrons when $B$ is into the page. Then electrons move in a circular orbit with $R_1 = {mv}/{qB}$ (can derive this equating the Lorentz force and the centripetal force).

Then, considering the geometry of the trajectory of electrons, we can apply the Law of Cosines and deduce that $OT^2 = 2R_1^2 (1 - \cos{2\alpha})\text{ } (*)$ .

Now consider the motion of electrons when $B$ is along $OT$ . The motion can be deconstructed into two components -- circular motion with period $T = {2\pi R_2}/{v \sin{\alpha}} = {2\pi m}/{qB}$ (here we derive $R_2$ in a similar way to $R_1$ , but taking $v\sin{\alpha}$ instead of $v$ ) and motion along $OT$ such that $OT^2 = t v^2\cos^2{\alpha} \text{ }(**)$ .

We can see $t$ has to be natural multiple of $T$ . In our case $\alpha$ is minimal when $v\cos{\alpha}$ is maximal hence for $OT$ to be minimal take $t = T$ . Therefore, equating $(*)$ and $(**)$ and substituting $t = T$ we get some nice cancellation of terms and end up with $2\pi^2 \cos^2{\alpha} = 1 - \cos{2\alpha}$ . Using some trig identities and keeping boundaries for $\alpha$ in mind, we can simplify this to $\cot{\alpha} = \frac{1}{\pi}$ .

Therefore $\alpha = \cot^{-1}{\frac{1}{\pi}} = \boxed{72.3^{\circ}}$ .