Honey jar and teddy bear

Probability Level 3

In the picture bellow: the bear want to go to the cell containing the honey jar, each time he move he go either to the up-left cell or up-right cell. However the bear prefer to go right more than to the left as shown.

What is the probability (in percentage) that the bear will go to the honey jar?

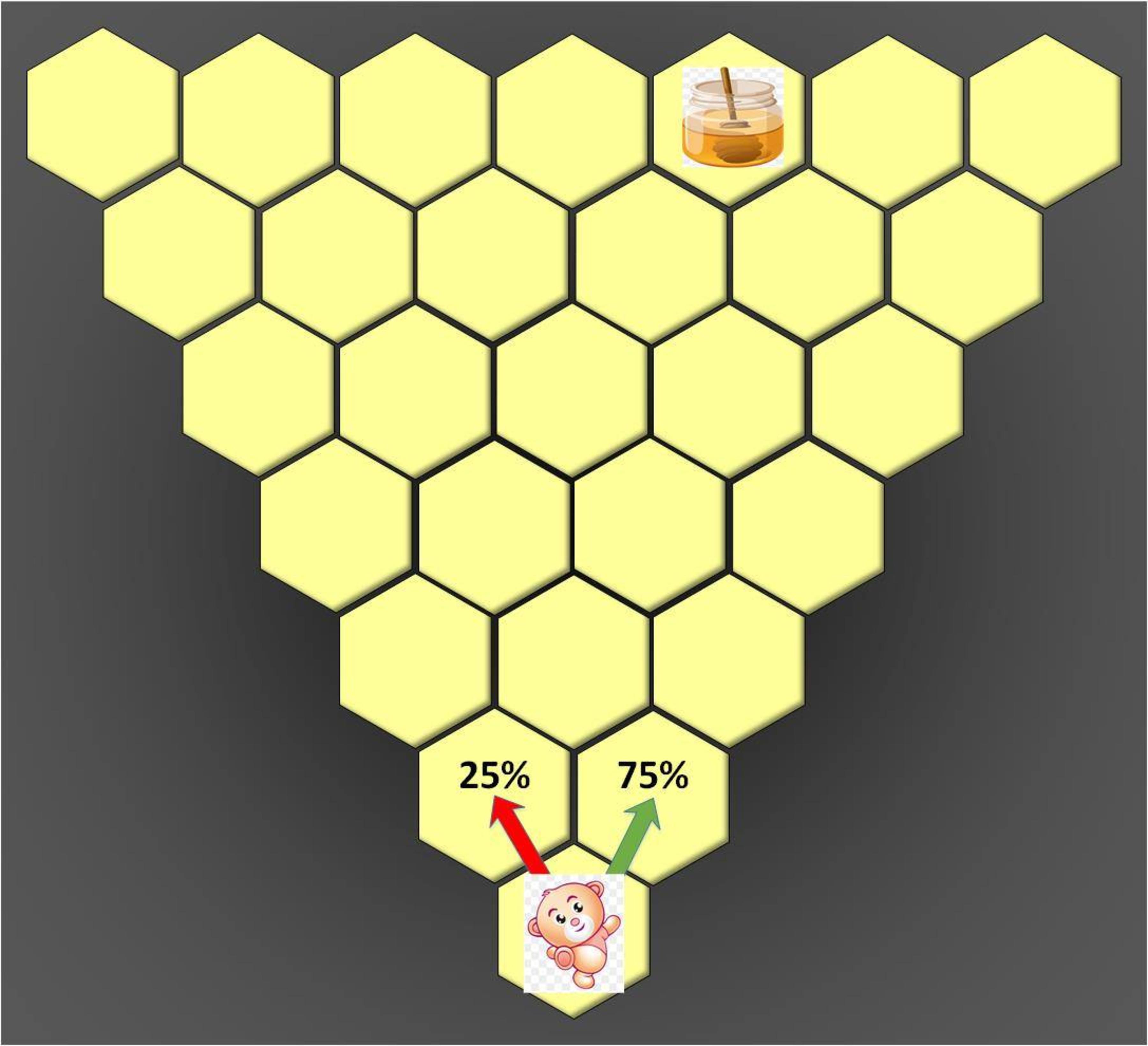
The answer is 29.663.

1 solution

David Vreken
Aug 25, 2019

There are $5 + 4 + 3 + 2 + 1 = {6 \choose 2} = 15$ ways the bear can get to the honey:

Since each path requires $2$ up-left steps and $4$ up-right steps, the probability is $15 (\frac{1}{4})^2(\frac{3}{4})^4 \approx \boxed{29.663 \%}$ .

Next problem. Where is pozition in upper line of the honey jar with maximum of the probability to meet with the bear?

Yuriy Kazakov - 1 year, 8 months ago

Letting $x = 0$ be the far left tile along the top and $x = 6$ be the far right tile along the top, then each probability is ${6 \choose x} (\frac{1}{4})^{6-x}(\frac{3}{4})^x$ which leads to:

Pos	Probability
$0$	${6 \choose 0} (\frac{1}{4})^{6-0}(\frac{3}{4})^0 \approx 0.024 \%$
$1$	${6 \choose 1} (\frac{1}{4})^{6-1}(\frac{3}{4})^1 \approx 0.439 \%$
$2$	${6 \choose 2} (\frac{1}{4})^{6-2}(\frac{3}{4})^2 \approx 3.296 \%$
$3$	${6 \choose 3} (\frac{1}{4})^{6-3}(\frac{3}{4})^3 \approx 13.184 \%$
$4$	${6 \choose 4} (\frac{1}{4})^{6-4}(\frac{3}{4})^4 \approx 29.663 \%$
$5$	${6 \choose 5} (\frac{1}{4})^{6-5}(\frac{3}{4})^5 \approx 35.596 \%$
$6$	${6 \choose 6} (\frac{1}{4})^{6-6}(\frac{3}{4})^6 \approx 17.298 \%$

which means position $x = 5$ (the tile second from the right) has the highest probability.

David Vreken - 1 year, 8 months ago

Ok. Thanks for attention. And there is 3D problem for piramide from cubes with N floors. In this case four probabilitis $P_0, P_1, P_2, P_3$ there are for transit from k-floor to (k+1)-floor , $P_0 + P_1 + P_2 + P_3 =1$ Find position with maximum probability for floor number N.

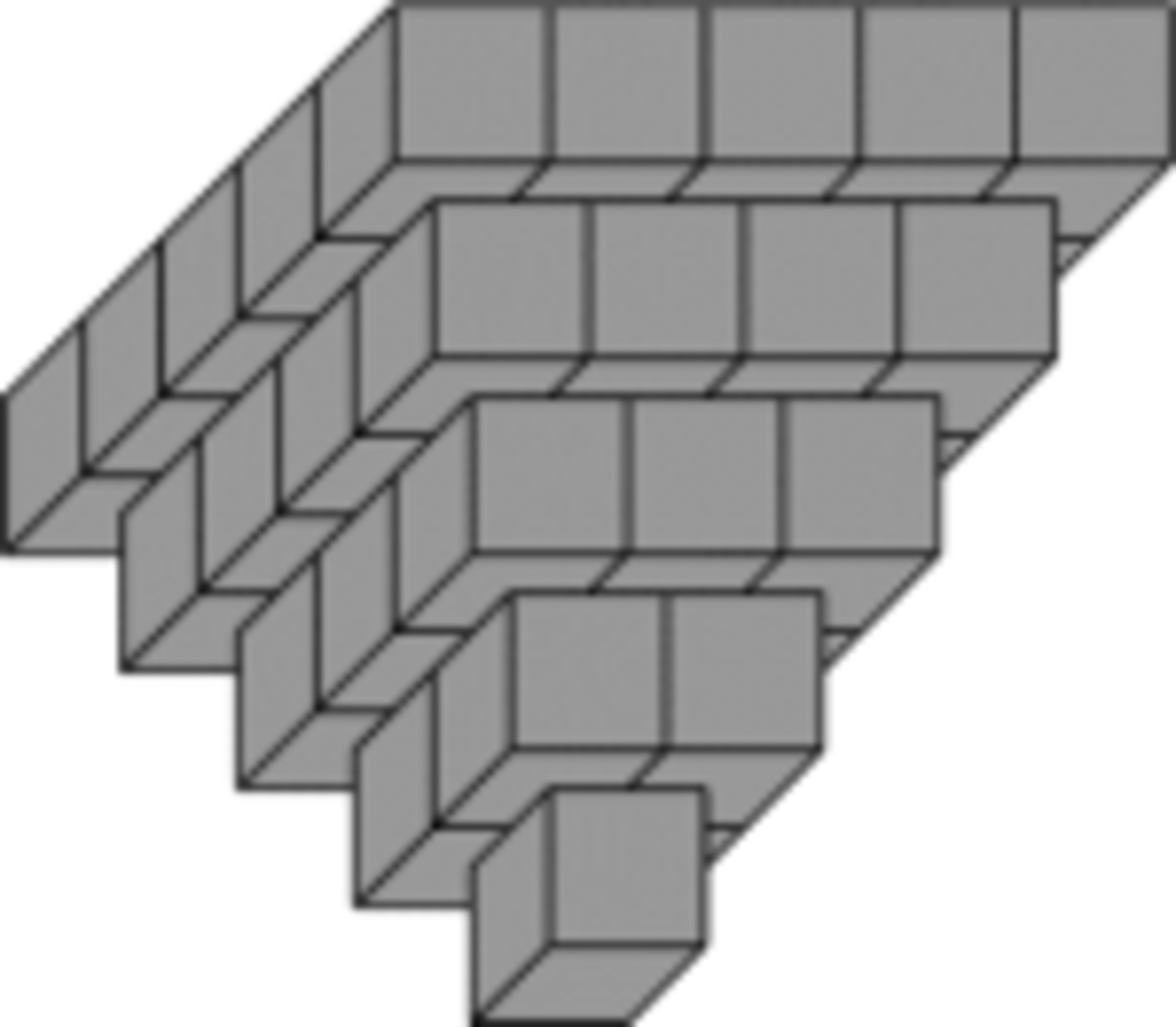
Or 3D problem for piramide from spheres with N floors. In this case three probabilitis $P_0, P_1, P_2$ there are for transit from k-floor to (k+1)-floor , $P_0 + P_1 + P_2 =1$ Find position with maximum probability for floor number N.

Yuriy Kazakov - 1 year, 8 months ago

@Yuriy Kazakov – Here are the probabilities for the first five floors of the square pyramid:

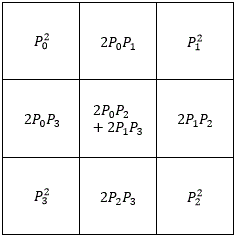
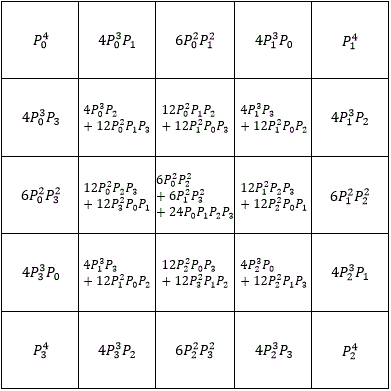
and it gets even more complicated after that (I couldn't come up with an explicit equation).

One observation using the 5th floor, 2nd row, and 2nd column as an example ( $4P_0^3P_2 + 12P_0^2P_1P_3$ ) is that $P_0^3P_2$ is one path to that box with a coefficient of $\frac{4!}{3!1!} = 4$ because there are $4$ steps with exponents $3$ and $1$ , and $P_0^2P_1P_3$ is another path to that box with a coefficient of $\frac{4!}{2!1!1!} = 12$ because there are $4$ steps with exponents $2$ , $1$ , and $1$ .

Another observation is that the each kth floor contains all the terms of the expansion $(P_0 + P_1 + P_2 + P_3)^{k - 1}$

David Vreken - 1 year, 8 months ago

@Yuriy Kazakov – Here are the probabilities for the first five floors of the triangular pyramid:

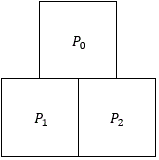
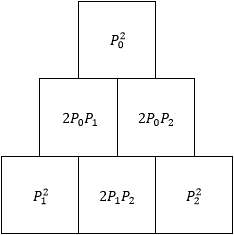
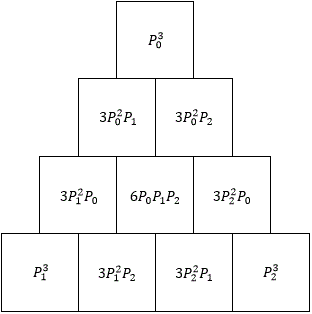
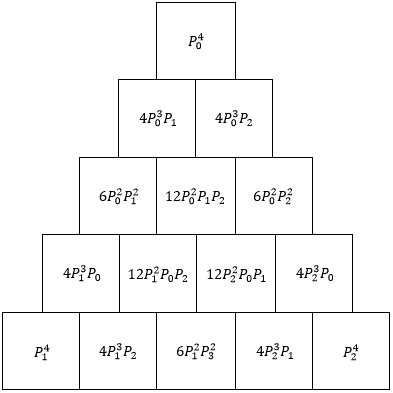
The kth floor contains all the terms in the trinomial expansion $(P_0 + P_1 + P_2)^{k - 1}$ . See Pascal's Pyramid for more information on trinomial expansions.

David Vreken - 1 year, 8 months ago

@David Vreken – Ok. Thanks for attention.

Yuriy Kazakov - 1 year, 8 months ago

Honey jar and teddy bear

The answer is 29.663.

1 solution

1 pending report

Vote up reports you agree with