Horizontal pinball

Classical Mechanics Level 4

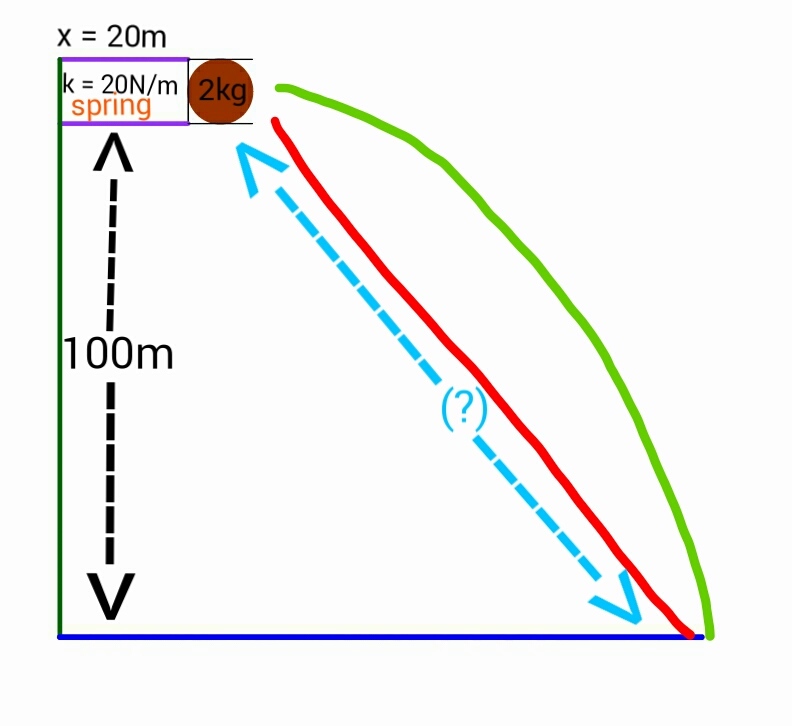
A ball of mass $2 \text{ kg}$ is placed in front of a spring having constant $20 \text{ N/m}$ and compression $20 \text{ m}$ at a height of $100 \text{ m}$ above the ground.

Now, the spring is released, giving the ball a horizontal velocity.

Find the total displacement (in meters) of the ball from the spring when it hits the ground.

Details and Assumptions:

The ball does not rebound after hitting the ground first.
Air friction is negligible.
The spring is 100% efficient.
Take $g=10 {\text{ m/s}}^2$ as the acceleration due to gravity.

The answer is 300.

1 solution

Ashish Menon
Jul 19, 2016

The energy given by the spring can be found out by $\dfrac{1}{2} {\text{kx}}^2\\ = \dfrac{1}{2}×20×400\\ = 4000 \text{J}$

Now, this energy converts into kinetic energy of the ball which is given by $\dfrac{1}{2} {\text{mv}}^2$ .
$\implies 4000 = \dfrac{1}{2} × 2 × {\text{v}}^2\\ \text{v} = \sqrt{4000}$

We proceed to find out the horizontal range of this projectile which is given by $\text{v}\sqrt{\dfrac{\text{2h}}{\text{g}}}\\ = \sqrt{4000} \sqrt{\dfrac{2×100}{10}}\\ = \sqrt{80000}$

So, the displacement can be found by using the Pythagoras' theorem which is the hyptoenuse in the right angled triangle having its legs as the horizontal range of the projectile and the initial height of the ball.

$\therefore$ Displacement = $\sqrt{{(100)}^2 + {(\sqrt{80000})}^2}\\ = \sqrt{90000}\\ = \color{#3D99F6}{\boxed{300 \text{m}}}$

I also did like this....

Sargam yadav - 4 years, 11 months ago

Nice! :) (+1)

Ashish Menon - 4 years, 11 months ago

Uh... if there's an extension in the spring it can't push the ball. It can only push it if there's a compression in the spring.

Abhilash Mukherjee - 4 years, 11 months ago

Woah, thanks, I fixed that typo-

Ashish Menon - 4 years, 11 months ago

can i ask why the ball suddenly comes to rest as soon as it touches the ground? '...a horizontal velocity. Find the final displacement (in metres) of the ball when it comes to rest...' I think that the ball will roll and hence will never stop.

Ajinkya Shivashankar - 4 years, 11 months ago

Plz read the first assumption under the head Details and assumptions

Ashish Menon - 4 years, 11 months ago

I think i made i very wrong i consider that the ball would have got the spring energy and it would have also the gravitacional energy and that would be equal to cinetc energy.then i thought velocity equal to square root of 6000 and as this would have velocity in both ways,horizontal and vertical,and the vertical velocity would be square root of 2000,so horizontal velocity would be equal to square root of 4000 so displacement in horizontal would be square root of 80000 and in vertical 100 and by pythagoras the displacement woulf be square root of 90000 whic is 300

Mr Yovan - 4 years, 10 months ago

Hmm, yeah though you got the correct answer, the procedure has a tiny mostake. Qhen the spring releases the ball in forward direction, the ball obtains only a horizontal velocity which remains constant throughout provided other acting forces are assumed negligible. Yes, gravitation certainly acts on it which makes it hit the ground in the first place. In other words, the velocity (or any other factpr) along the x-axis and y-axis is not related to each other. But certainly a good try :) Hope you would the correct answer with the correct steps next time.

Ashish Menon - 4 years, 10 months ago

Thanks man ,i got to improve my physics to dont make huge mistakes again

Mr Yovan - 4 years, 10 months ago

@Mr Yovan – We all make mistakes. :) Once I made earth rotating about its own axis with a speed of 365 hours per day. (You can imagine where I went wrong :P) Anyways hoping to see new elegant solutions from you in future. :)

Ashish Menon - 4 years, 10 months ago

Horizontal pinball

The answer is 300.

1 solution

0 pending reports