How To Cut This Square?

We are given:

$\begin{aligned} \text{area of 36 squares with side 1}&+\text{area of 1 square with side x}\\ &=\text{area of the original square with side y} \end{aligned}$

$\begin{aligned} 36+x^2&=y^2\\ 6^2+x^2&=y^2 \end{aligned}$

We can observe that this forms a Pythagorean triplet, and we know that the general formula for the Pythagorean triplet is: $(2m)^2+(m^2-1)^2=(m^2+1)^2$

Substituting $m=3$ , we get; $\begin{aligned} (2\times 3)^2+(3^2-1)^2&=(3^2+1)^2\\ 6^2+8^2&=10^2 \end{aligned}$

Thus, $x=8$ and $y=10$ . Hence the side of the original square was $10\text{ cm}$ .

From the question we have area of 36 unit squares+area of a square with side $y$ =area of bigger square with side $x$ $\Rightarrow 36+y^2=x^2$ On rearranging and factorising we get $\Rightarrow (x+y)(x-y)=36$ Now we could factor out 36 in a number of ways like 1×36 or 2×18 or 3×12 etc. But only 2×18 yield positive whole number solutions for $x$ & $y$ i.e. $\Rightarrow (x+y)(x-y)=18×2 \Rightarrow$ x+y=18 and $\Rightarrow$ x-y=2 This leads us to $x$ or length of bigger side as $\boxed{10}$

Since the original figure is a square, it's area is a squared number. Since the 36 squares have an area of 1 square cm, the sides of each square (the 36 squares) is 1 cm. Their total area is 36 square cm. From the choices, if you subtract 36 from them the answer should be a perfect square.

10 * 10 = 100

100 - 36 = 64

64 = 8^2

8 is the side length of the larger square

and 10 cm is the side length of the original square

Relevant wiki: Length and Area Problem Solving

Let the $37^{th}$ or the larger square to have a side length $m$ ; $m$ must be a natural number otherwise the $36$ $1\text{-cm}^2$ squares cannot be laid beside it to have straight edges. The $37$ squares can put together to form the original square as follows, where the larger square is in pink and the blue region is covered by the $36$ $1\text{-cm}^2$ squares. Again $n$ must be a natural number.

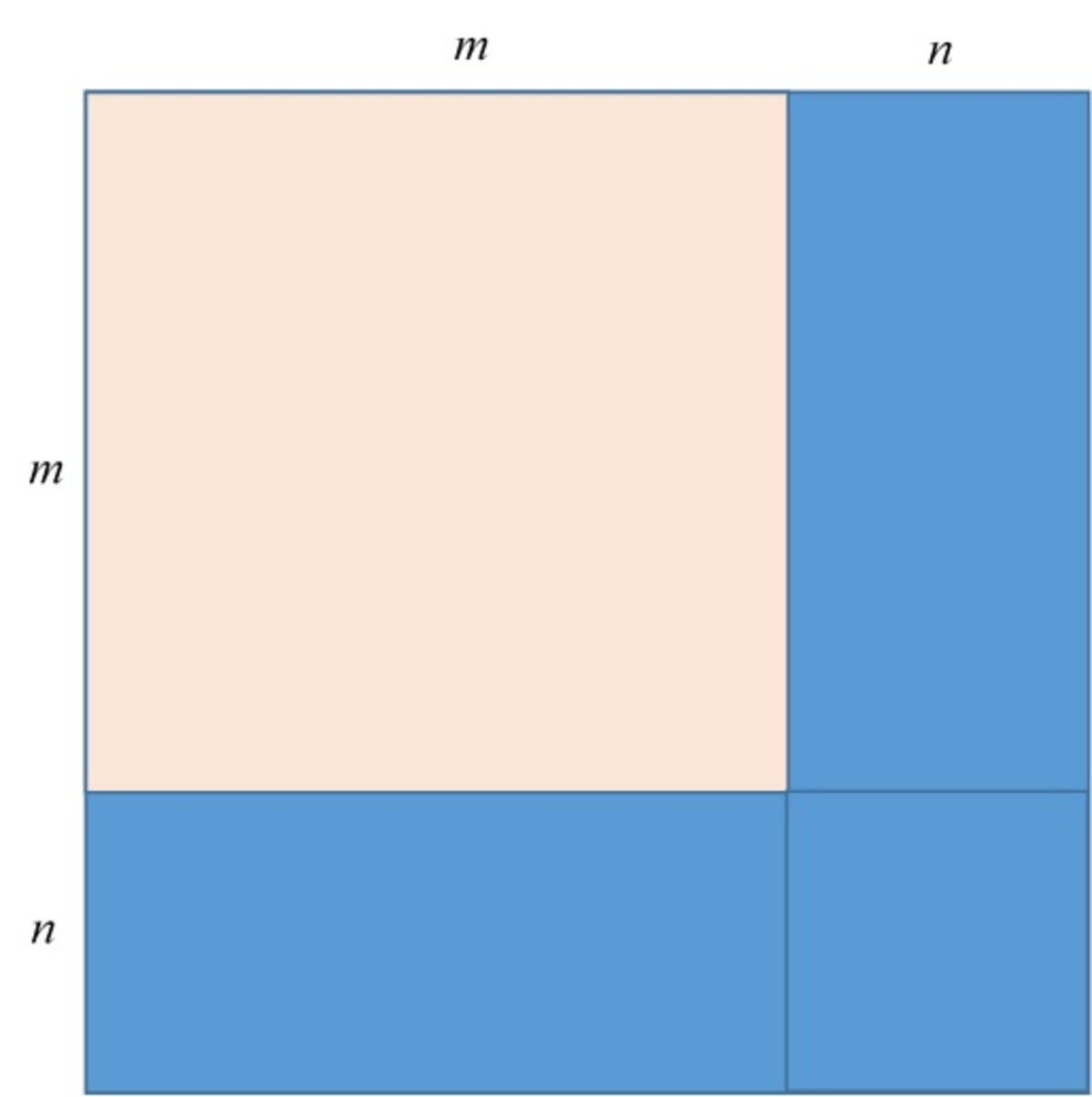
We note that: $n^2 + 2mn = 36 \quad \Rightarrow m = \dfrac{36-n^2}{2n} = \dfrac{(6-n)(6+n)}{2n}$ . It can be seen that for integer $m$ , $n$ must be even and for $m > 0$ , $n < 6$ .

Therefore, $n$ can only be $2$ or $4$ $\Rightarrow \begin{cases} n = 2 & \Rightarrow m = 8 \\ n = 4 & \Rightarrow \color{#D61F06}{m = 2.5 \text{ rejected}} \end{cases}$

So the side length of the original square is $m+n = 8+2 = \boxed{10}$