How fast is this dog?
A thief escapes from a prison. When he was at a distance of 5km from the prison, the police start chasing him with a speed of 20m/s. The thief is running away with speed 10m/s. A police dog starts running as soon as the police starts, with a speed of 30m/s and runs back and forth from the police to the thief and back to the police till the police catch the thief.
In kilometers, find the distance that the dog ran in the forward direction only.
The answer is 12.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How is the difference between the the forward distance and backward distance equal to 20T ??
Log in to reply
Because it's equal to the displacement of the dog which is equal to the displacement of the police.
Log in to reply
Thank You for your reply!!!!
I don't understand why they're equal. Can you explain further?
Log in to reply
@Saya Suka – Well, the displacements of the dog and the police are equal because they start and end at the same point. The reason L f ± L b equal to the above expressions simply come from the definitions and the fact that "velocity" changes sign when the dog turns but "speed" doesn't.
Beautiful problem...but a philosophical question. Even though there is a finite total time of 500 seconds to capture the thief, does not the dog have an infinite number of intercepts as this is an infinite series that converges to 10000 net meters forward over 500 seconds?
Log in to reply
Bonus problem, what if it took the dog t seconds to turn around, how would the distance here change as a function of t?
That is what intrigued me too ... Because i couldn't solve it in one go and started number crunching. And after 10 intercepts noticed that though the dog's trips get smaller in distance ,they never end. So I added all the forward distances found to me and it was 12.18 ....So i guessed that 12.5 would be the limit.
Lf- distance moved in forward direction by dog Lb- distance moved in backward direction by dog T-Total time traveled by dog and police. 5 km=5000m 5000+10T=20T 5000=10T T=500 seconds Total distance moved =20T= 10000m Lf-Lb =10000 Lf+Lb= 30 T Adding, 2Lf=10000+30T 2Lf=10000+30*500 2Lf=25000 Lf=12500
This is a very nice question. My question is, why does the dog runs back and forth from the police to the thief and back to the police till the police catch the thief?
Actually i noticed that the dog makes infinite trips back and forth before finishing. Just like the zeno's paradox.
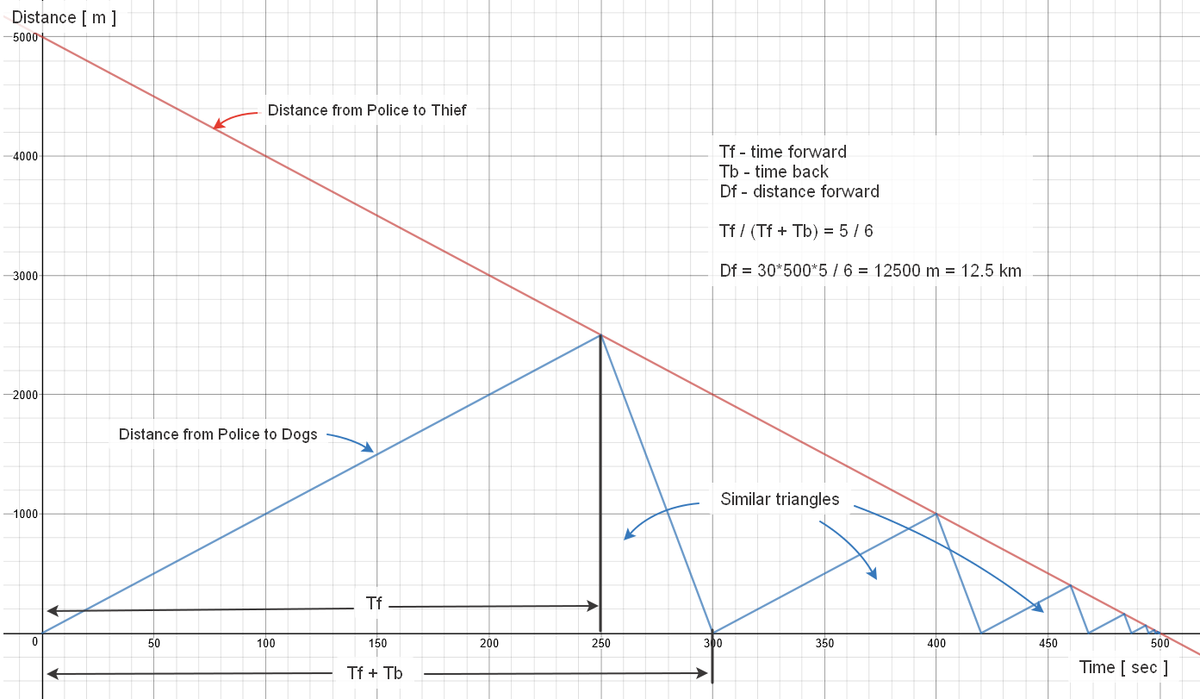

Actually it should be in classical mechanics category but anyway let solve it more physics!!
we only have one time interval because dog, police and thief share the same duration and let it be T.
Let L f be the total distance that dog goes forward and L b is a total distance that dog goes backward.
Then we have these equations
2 0 T = 5 0 0 0 + 1 0 T
L f + L b = 3 0 T
L f − L b = 2 0 T
So if we plus the two below equation, we have
2 L f = 5 0 T then L f = 2 5 T
since T = 5 0 0 s
L f = 1 2 5 0 0 m = 1 2 . 5 k m
1 2 . 5