How likely is it to get an acute angle?

Probability Level 2

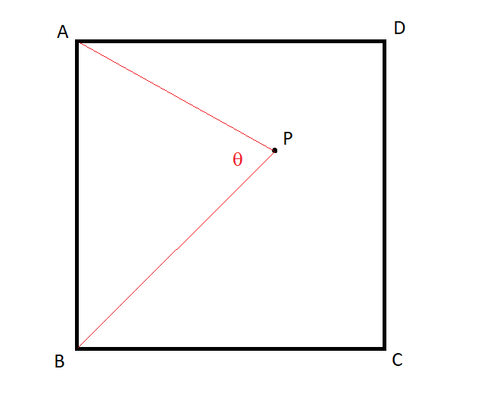
$ABCD$ is a square; and $P$ is a point inside it. What is the probability that $\theta = \angle APB$ is acute?

The answer is 0.6073.

3 solutions

Chew-Seong Cheong
Sep 6, 2020

We note that $\theta = 90^\circ$ when point $P$ is on a semicircle. If $P$ is within the semicircle, $\theta$ is obtuse. If $P$ is outside the semicircle (the shaded region), $\theta$ is acute. Let $ABCD$ be a unit square. Then the probability that $\theta$ is acute

$P = \text{the area of the shaded region} = 1 - \frac \pi 8 \approx \boxed{0.607}$

This question is for Chew-Seong Cheong. Sir, How do we calculate the probability that Theta is exactly a right-angle?

Vijay Simha - 9 months ago

Zero. It has no area.

Chew-Seong Cheong - 9 months ago

I want to know this too, (Vijay's question), considering it's a sliver of length instead of a bound or an area

A Former Brilliant Member - 9 months ago

Zero. It has no area.

Chew-Seong Cheong - 9 months ago

P can lie on both a line and a surface. Is only the 'mathematical' probability zero and it might actually be possible, or does zero here mean it is actually impossible?

A Former Brilliant Member - 9 months ago

@A Former Brilliant Member – Interesting...

Mathematically it should be 0.

But, intuitively (a bit absurd argument for true mathematical minds), there are infinite points along the circumference of the circle. And there are infinite points within the square as well. Are these two infinities, comparable? Does that make $\dfrac{\infty}{\infty} = 1$ ?

The real answer if probability works out to be 0, then means it is impossible, right? I recommend watching 3b1b's video. I haven't completely understood, I will try to watch again and come up with a conclusion if possible

Mahdi Raza - 9 months ago

@Mahdi Raza – I just watched the video you suggested, it's great, thanks for recommending

A Former Brilliant Member - 9 months ago

@A Former Brilliant Member – Not impossible but probability tense to infinitesimal $P(x) \to dx$ . We are talking about continuous variable and we use integral to calculate probability $Pr (a \le X \le b) = \int_a^b p(x) \ dx = P(b) - P(a)$ , so $Pr \left(\frac \pi 2 \le X \le \frac \pi 2 \right) = \int_\frac \pi 2^\frac \pi 2 p(x)\ dx = P \left(\frac \pi 2\right) - P \left(\frac \pi 2 \right) = 0$ . That is why if you use a statistical table you have to look for two values and deduct. We can't talk about probability of a point but a range. For discrete probability for example the probability to roll a 3 out of a fair die is $\frac 16$ is correct because the total possible outcomes is 6 and 3 is one of them. In our case here, the total outcomes for $0^\circ \le \theta \le 180^\circ$ is infinite. therefore, the probability of $\theta = 90^\circ$ is $\frac 1\infty = 0$ . Which is actual true in real life. Can we draw an angle exactly $90^\circ$ ? Actually it is impossible. We can only draw an angle of $90^\circ \pm \epsilon$ to a certain accuracy.

Chew-Seong Cheong - 9 months ago

@Chew-Seong Cheong – That is a very good answer. Thanks!

Mahdi Raza - 9 months ago

@Chew-Seong Cheong – Thanks for explaining, I doubted that too, a point is infinitesimally small, hence infinite amount of points lie on the square, I was about to call it 'multidimensional' probability

A Former Brilliant Member - 9 months ago

Thanks Chew-Seong Cheong for the explanation

Vijay Simha - 9 months ago

A Former Brilliant Member
Sep 6, 2020

Since in $\triangle ABP, \theta$ will not be acute beyond the bound where it becomes a right triangle, we need to see where are the bounds of $\theta$ being $90$ , once we consider the side of the square to be $s$ and that the furthest bound of $\theta = 90$ is when it's isosceles right triangle we see it's $\frac{s}{2}$ away or where both diagonals intersect. We can refer Thales Theorem to figure that $s$ being the largest side, the shape must be a semicircle with radius $\frac{s}{2}$ , on the semicircle, $\theta$ is $90$ , inside it, it's obtuse, outside it, it's acute .

The area outside the semicircle is $s^2 - \frac{\pi}{2}\frac{s^2}{2^2}$ , and the required probability of having this area out of the total area of $s^2$ is

$\dfrac{s^2[ 1 - \frac{\pi}{2}\frac{1}{2^2}]}{s^2} = 1 - \dfrac{\pi}{2}\dfrac{1}{2^2}= \boxed{0.6075}$

What about a circle

Ron Gallagher
Sep 9, 2020

Choose a coordinate system so that B is at the origin and A is at point (0,1). Let the coordinates of P be (x,y). (0 < x < 1 and 0 < y < 1, since P is inside the square). Consider the vectors PA = (-x, 1-y) and PB = (-x, -y). If theta is the angle between these vectors, we find that theta is less than 90 exactly when cos(theta) > 0, or when the dot product between PA and PB is greater than zero. But, a calculation shows that the dot product between PA and PB is x^2 + y^2 - y = x^2 + (y-1/2)^2 - 1/4. We then see that this quantity is greater than zero if

x^2 + (y-1/2)^2 > 1/4.

Since P lies in the square, this inequality represents the locus of points that lie outside a semicircle of radius 1/2 centered at (0,1/2) but inside the square

Probability Theta is acute = (area of square - area of semicircle of radius 1/2) / (area of square) = 1 - Pi/8 = .607 (approximately).

How likely is it to get an acute angle?

The answer is 0.6073.

3 solutions

0 pending reports