How long will you chase?
A boy runs on a circular path of radius R = 2 8 meters with constant speed u = 4 m/s .
Another boy starts from the center of the circle to catch the first boy. The second boy always moves towards the first one. and maintains a speed of v = 4 m/s . How long will the chase last in seconds?
Details and Assumptions :
1) Ignore air friction.
2) Take π = 7 2 2 .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Firstly I was Try to use Realtive concept , But it get's complicated and Then I did Same You , And Tushar it is really Interesting Question , Thanks for sharing it ! Also Just wanted to know How did you solved it ?
@tushar very nicce problem and nice solution by @satvik
Log in to reply
Thanks bro! :)
Log in to reply
please recommend me any books that you think have been helpful for Mechanics and Em
Log in to reply
@Mardokay Mosazghi – For solving problems Irodov and Understanding Physics by DC Pandey are nice. But I am not sure if you can find them In US. You can buy Classical Mechanics by David Morin. for learning new concepts and solving even tougher problems.
Log in to reply
@Satvik Pandey – yes I got the classical mechanics book by Mr Morin, the problems are really tough and hard, do you think HC Verma as good as DC Pandey's book?
Log in to reply
@Mardokay Mosazghi – I think DC Pandey is better than HC Verma in terms of problems.
Log in to reply
@Satvik Pandey – Yes, DC pandey is better...much better....for mechanics and EM, not for optics, Thermodynamics and Modern physics
Log in to reply
@Tushar Gopalka – Are you giving JEE this year?
Log in to reply
@Satvik Pandey – Yeah but my Chem and Maths is weak which I have to improve. My main aim is to get into IISC, which is quite tough through JEE. I regret not giving KVPY....
Log in to reply
@Tushar Gopalka – I am in class 10 at present. I am in dilemma, which optional subject should I choose for class 12 boards? What is your suggestion?
Is there any way to get into IISC through JEE? `I don't know much about admission procedures in IISC.
@Satvik Pandey – ok thanks bro :D
Nice solution.
Thanks for the new concept that i can learn :D,i ussualy use relative concept haha
How did you get the equation of velocities in polar coordinates
I kind of ran into an ambiguity about the given solution. If both the boys have the same angular velocity, then both the boys and the center of the track always lie on a straight line, and the radial velocity of the second boy points towards the first boy and therefore, the resultant velocity of the boy does not point towards the other. Although in the given solution, the boy always moves towards the boy on the circumference in the radial direction, I think it would be more proper if the resultant velocity of the boy always points towards the first one (direct implication of the conditions given in the question). Using this logic too, one gets the same answer.
Why Vt=xw?
u have to put the detail that is both boys have equal angular velocities in assumptions
I actually did this a little differently.
First, notice that "The second boy always moves towards the first boy" necessarily implies that, if v 1 is the velocity of the boy at the center and v 2 is the velocity of the boy at the edge, we must have:
v 1 ⋅ v 2 = 0 since the two are always normal. If we let:
v 2 = ( v cos ( r v t ) , v sin ( r v t ) ) and let:
v 1 = ( d t d x , d t d y )
It becomes clear that: d t d x = − tan ( r v t ) d t d y
If we use the additional facts that ∥ v 1 ∥ = v and x ( 0 ) = 0 , y ( 0 ) = 0 , we eventually arrive at:
r v t = 2 π which immediately leads to t = 1 1
sir I did is quite similarly nice solution
This is wrong if we don't assume same angular momentum, which we don't.
Also, it can be seen that at any instant the second boy's direction is towards the first boy. Hence, by symmetry the path described by the second boy will also be a circle of R= 14m. and he will catch the first boy by travelling half of this circle. Hence T= ((22/7) * 14 )/4 = 11sec. Note: the tangent drawn to the new circle will always direct towards second boy.
You are right but you need to prove that indeed the second boy goes in a circular path.
Log in to reply
second boy should go in circular path tushar as it is given that he is always moving towards first boy.......and changing path at every point with respect to boy moving in circle...
i diid it in exact same way.............this is preety straight forward if we imagine aproching boys path......
I don't understand how the second boy covers a circle of 14m
The problem can be made a little more interesting if the boy on the circular path can change his direction at any time. The end result is nonetheless the same.
Thats true. But where did you write down the solution? :D
Log in to reply
Here's the "solution without words", which I did quite some time ago. It applies here.
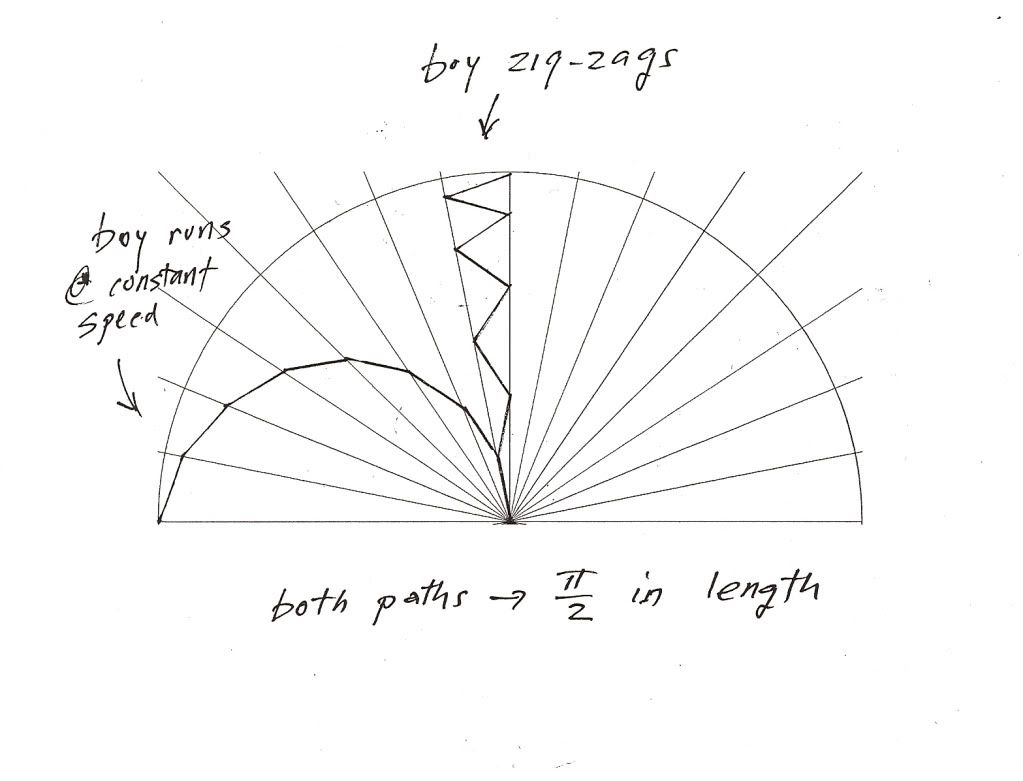 The Chase
The Chase
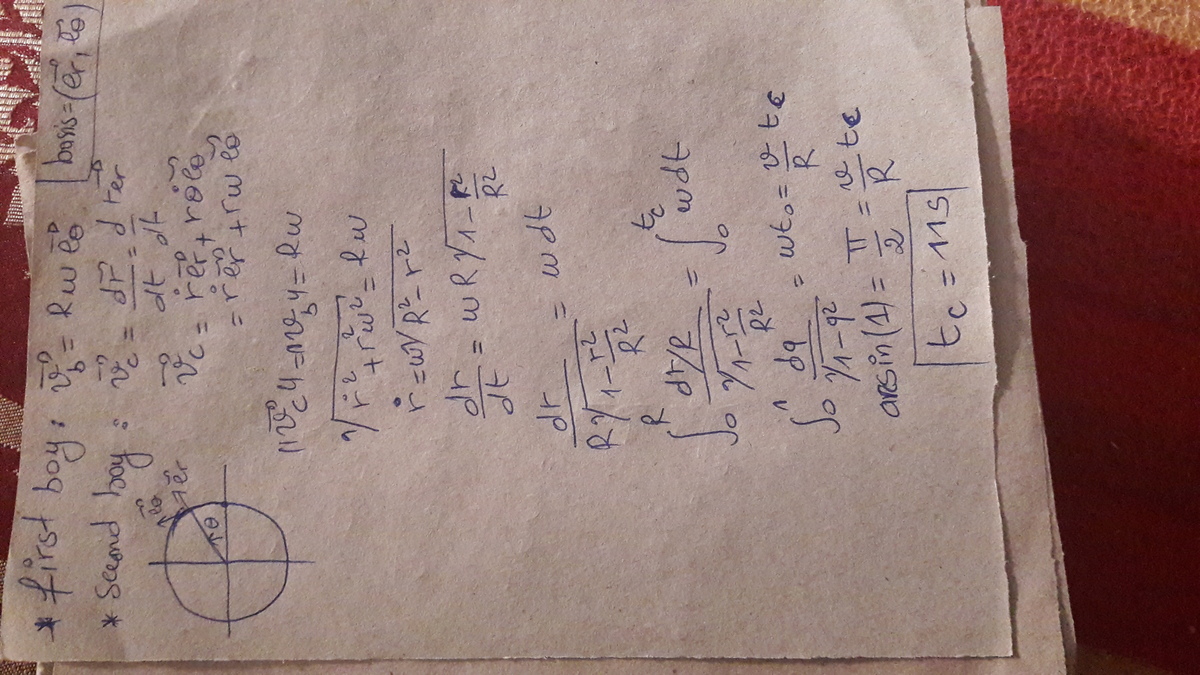
This problem can be solved easily if the angular velocity of the two boys are equal about the center of the circle.
Now in polar coordinates square of total velocity ( V ) = Sum of the squares of radial ( V ϕ )+Tangential velocity (( V t ) of the body.
So V 2 = V ϕ 2 + V t 2
Let at time 't' the boy(who is chasing) be at a distance 'x' from the center.
So V t = x ω
Now ω = R u (Remember ω is same for both boys and v = u )
So v 2 − ( R x v ) 2 = V ϕ
or v 2 − ( R x v ) 2 = d t d x
or R v t = ∫ 0 2 8 R 2 − x 2 d x
So R v t = 2 π
On solving we get t = 1 1 s e c