How Low Can You Get?
 A small particle
P
of mass
m
is sliding on the surface of a rough hemispherical shell of radius
a
, which is fixed to the horizontal ground. The coefficient of friction between the particle and the hemisphere is
2
1
. The particle starts at the top
T
of the sphere, travelling horizontally with initial speed
a
ω
, where
ω
>
0
. There is a constant gravitational force of
m
g
acting vertically downwards on the particle. One of three things might happen:
A small particle
P
of mass
m
is sliding on the surface of a rough hemispherical shell of radius
a
, which is fixed to the horizontal ground. The coefficient of friction between the particle and the hemisphere is
2
1
. The particle starts at the top
T
of the sphere, travelling horizontally with initial speed
a
ω
, where
ω
>
0
. There is a constant gravitational force of
m
g
acting vertically downwards on the particle. One of three things might happen:
- the particle slides on the hemisphere until it comes to rest a height h > 0 above the ground,
- the particle slides on the hemisphere until it reaches a height h > 0 above the ground, at which point it leaves the surface of the hemisphere,
- the particle slides on the hemisphere all the way until it reaches the ground, keeping in contact with the hemisphere at all times, reaching a height h = 0 above the ground.
depending on the value of ω . In each case, h is the lowest height above the ground attained by the particle while still in contact with the hemisphere. What is the infimum of the value of h as ω varies? Your answer will be k a for some constant k ≥ 0 ; give the value of k .
The answer is 0.48484014.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase
sir nice solution, I just upvoted.
BTW what is the meaning of ‘infimum’ in the problem?
Log in to reply
Thanks. Basically, it means "minimum"
Log in to reply
@Steven Chase As I predicted while solving.
Log in to reply
@A Former Brilliant Member – Another phrase for infimum is greatest lower bound. The infimum of a set is the largest number less than or equal to all members of that set. Thus the infimum of the set of strictly positive reals is 0 , but of course that set has no minimum.
In this case, we cannot actually achieve a lowest height of a cos θ 1 , since if we use the value α 0 , the particle stops sooner. However, we can achieve any height greater than a cos θ 1 .
Log in to reply
@Mark Hennings – @Mark Hennings Thankyou sir
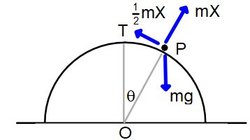 Let
θ
be the angle
∠
T
O
P
. While the particle is in contact with the hemisphere and still moving, the particle will experience a normal reaction
m
X
and a frictional force
2
1
m
X
as indicated in the diagram (note that the motion is, essentially, two-dimensional). We note that
θ
=
0
and
θ
˙
=
ω
at time
t
=
0
. For convenience, we introduce the dimensionless parameter
α
>
1
, where
a
ω
2
=
2
1
(
α
−
1
)
g
.
Let
θ
be the angle
∠
T
O
P
. While the particle is in contact with the hemisphere and still moving, the particle will experience a normal reaction
m
X
and a frictional force
2
1
m
X
as indicated in the diagram (note that the motion is, essentially, two-dimensional). We note that
θ
=
0
and
θ
˙
=
ω
at time
t
=
0
. For convenience, we introduce the dimensionless parameter
α
>
1
, where
a
ω
2
=
2
1
(
α
−
1
)
g
.
The position vector, velocity and acceleration of the particle are r = a ( cos θ sin θ ) r ˙ = a θ ˙ ( − sin θ cos θ ) r ¨ = a θ ¨ ( − sin θ cos θ ) − a θ ˙ 2 ( cos θ sin θ ) so we get the equation of motion m a θ ¨ ( − sin θ cos θ ) − m a θ ˙ 2 ( cos θ sin θ ) = m X ( cos θ sin θ ) − 2 1 m X ( − sin θ cos θ ) + m g ( − 1 0 ) Taking radial and transverse components, we obtain a θ ¨ = − 2 1 X + g sin θ − a θ ˙ 2 = X − g cos θ Eliminating X from these equations, we obtain a ( 2 θ ¨ − a θ ˙ 2 ) d θ d [ a θ ˙ 2 e − θ ] a θ ˙ 2 e − θ = g ( 2 sin θ − cos θ ) = g ( 2 sin θ − cos θ ) e − θ = A − 2 1 g ( 3 sin θ + cos θ ) e − θ for some constant A . Applying our initial conditions, it follows that A = 2 1 g + a ω 2 = 2 1 g α , so we deduce that a θ ˙ 2 e − θ X e − θ = 2 1 g [ α − ( 3 sin θ + cos θ ) e − θ ] = 2 1 g [ 3 ( sin θ + cos θ ) e − θ − α ] Thus motion continues provided that θ ˙ > 0 and X > 0 , so provided that f ( θ ) < α < g ( θ ) , where f ( θ ) = ( 3 sin θ + cos θ ) e − θ g ( θ ) = 3 ( sin θ + cos θ ) e − θ Even if it were true that θ ˙ > 0 for all 0 ≤ θ ≤ 2 1 π , the fact that X = − a θ ˙ 2 < 0 when θ = 2 1 π means that X will become zero, and so the particle will leave the surface, before it reaches the ground. Thus the third option given in the question never occurs. To make the final height h as small as possible, we want to be able to reach as large a value of θ as possible.
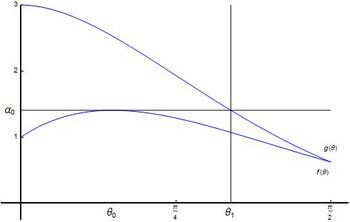 We note that
f
(
θ
)
<
g
(
θ
)
for all
0
<
θ
<
2
1
π
. Moreover
f
′
(
θ
)
=
2
(
2
cos
θ
−
sin
θ
)
e
−
θ
, and so
f
(
θ
)
reaches a maximum at
θ
=
θ
0
=
tan
−
1
2
1
. On the other hand
g
′
(
θ
)
=
−
6
sin
θ
e
−
θ
, and so
g
is strictly decreasing on
(
0
,
2
1
π
)
. Define
α
0
=
f
(
θ
0
)
≈
1
.
4
0
6
4
5
3
5
8
. If
1
<
α
≤
α
0
, then the particle comes to rest on the hemisphere, and the maximum value of
θ
is achieved is the solution of
f
(
θ
)
=
α
that is less than or equal to
θ
0
. Thus no value of
θ
greater than
θ
0
is possible in this case. If
α
0
<
α
<
3
then the particle does not stop, but eventually leaves the hemisphere when
θ
=
g
−
1
(
α
)
. If
α
≥
3
then the particle leaves the hemisphere immediately, and so the largest value of
θ
that is achieved is
0
. Thus the supremum of the values of
θ
that can be achieved is
θ
1
=
g
−
1
(
α
0
)
≈
1
.
0
6
4
6
1
5
9
5
. Thus the infimum of the final height above ground that can be achieved is
a
cos
θ
1
, so that
k
=
cos
θ
1
=
0
.
4
8
4
8
4
0
1
4
.
We note that
f
(
θ
)
<
g
(
θ
)
for all
0
<
θ
<
2
1
π
. Moreover
f
′
(
θ
)
=
2
(
2
cos
θ
−
sin
θ
)
e
−
θ
, and so
f
(
θ
)
reaches a maximum at
θ
=
θ
0
=
tan
−
1
2
1
. On the other hand
g
′
(
θ
)
=
−
6
sin
θ
e
−
θ
, and so
g
is strictly decreasing on
(
0
,
2
1
π
)
. Define
α
0
=
f
(
θ
0
)
≈
1
.
4
0
6
4
5
3
5
8
. If
1
<
α
≤
α
0
, then the particle comes to rest on the hemisphere, and the maximum value of
θ
is achieved is the solution of
f
(
θ
)
=
α
that is less than or equal to
θ
0
. Thus no value of
θ
greater than
θ
0
is possible in this case. If
α
0
<
α
<
3
then the particle does not stop, but eventually leaves the hemisphere when
θ
=
g
−
1
(
α
)
. If
α
≥
3
then the particle leaves the hemisphere immediately, and so the largest value of
θ
that is achieved is
0
. Thus the supremum of the values of
θ
that can be achieved is
θ
1
=
g
−
1
(
α
0
)
≈
1
.
0
6
4
6
1
5
9
5
. Thus the infimum of the final height above ground that can be achieved is
a
cos
θ
1
, so that
k
=
cos
θ
1
=
0
.
4
8
4
8
4
0
1
4
.
@Mark Hennings
Good problem
I also solved this way only.
Sir can you upload more problems like this ?
Indeed, a nice problem. Thanks for posting
Log in to reply
@Karan Chatrath
Sir which method you follow for this problem
MATLAB Or Analytical?
Log in to reply
I performed the theory, and then used Mathematica to do the numerical calculations...
Log in to reply
@Mark Hennings
–
@Mark Hennings
sir is it free?? Does it work in mobile and computer both??
Can you show your work in Mathematics?
Thanks in advance.
Log in to reply
@A Former Brilliant Member – Mathematica is not free, but Wolfram Alpha is. I only used it to calculate the value of θ 1 , since I know exact expressions for θ 0 = tan − 1 2 1 and α 0 = 5 e − θ 0 . Having defined the function g ( t ) and calculated α 0 , all I had to type was
FindInstance[{g[t] == alpha0,0 < t < pi/2},t]
to get the desired value of θ 1 . In Wolfram Alpha you would simply type in the explicit formulae for g and α 0 inside the FindInstance command.
Log in to reply
@Mark Hennings
–
@Mark Hennings
sir do you have purchased mathematics???
I checked it on website.
Sir i am just asking you have purchases it for what pupose Industry, education, Home and hobby???
I also wants to purchase??
Is it good for me to buy??
Thanks in advance.
Hope I am not disturbing you.
Log in to reply
@A Former Brilliant Member – As a teacher, I have an educational licence. Even so, it is quite expensive, but it is much better than WA.
Log in to reply
@Mark Hennings
–
@Mark Hennings is it 533 pounds per year???
I am a school student , for me it is 9 US dollar.
Sir in your opinion , will it help?
Can you tell me its features?
Log in to reply
@A Former Brilliant Member – To be honest, it will probably not be as much help to a school student as a good graphical calculator - you won't be able to use it in exams! If you want to spend $7 for your own fun, that is up to you. I do not spend anything like £533 a year on it!
Log in to reply
@Mark Hennings
–
@Mark Hennings
yes sir it will be like a cheating in exam.
But can I get solution of hard math questions, I have used wolfram, is it similar with that or have some extra features?
How much do you spend on mathematica in one year?
Thank in advance.
@Mark Hennings
can you help me in solving this equations
Thanks in advance.
I took an empirical approach, sweeping the initial angular velocity over a range. For each initial angular velocity, a time-domain simulation was run until one of the three termination conditions was reached. With a radius of 1 , I ended up with a minimum height of h m i n ≈ 0 . 4 8 5 occurring at initial angular speed ω 0 ≈ 1 . 4 2 6 . The angle θ is taken with respect to the vertical.
Below is a plot of initial angular speed vs the minimum height. If the particle has very little speed initially, it doesn't travel far along the surface, and ends up with a height close to the radius of the sphere. If the particle has very high speed initially, it more or less immediately flies off, resulting in a large final height. Only when the initial speed is at an intermediate value is the final height minimized.