How Many Dots?

Number Theory Level 4

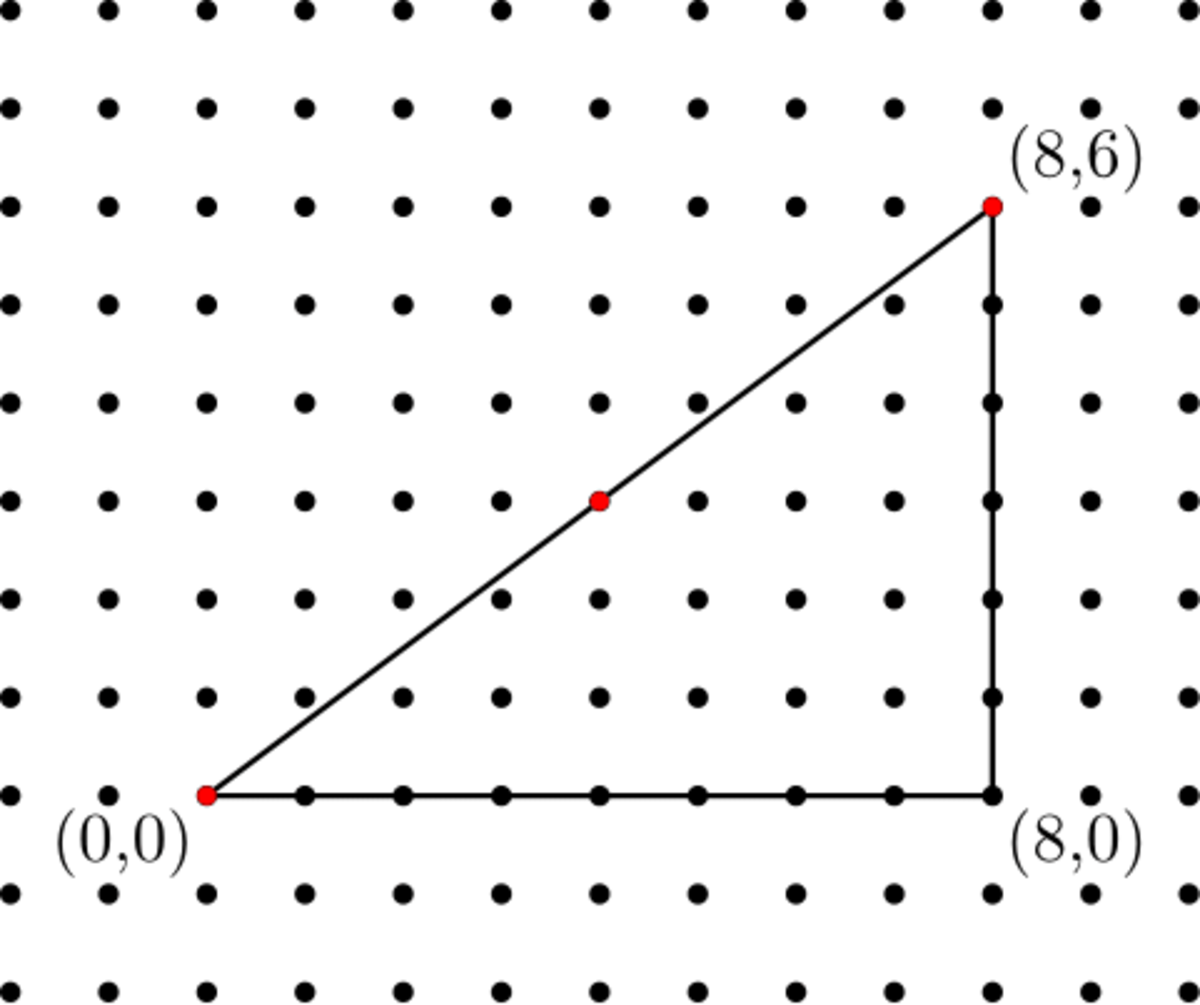
In the image above, 3 dots from the grid (marked red) lie on the hypotenuse of the right triangle. If the legs of the triangle were 36750 units and 35672 units, respectively, instead of 8 units and 6 units, how many dots from the grid would lie on the triangle's hypotenuse?

Fewer than 100 Exactly 100 More than 100

1 solution

展豪張
Mar 22, 2016

Number of dots lying on the hypotenuse $=\gcd(36750,35672)+1=99$

But why ? :)

Chirayu Bhardwaj - 5 years, 2 months ago

Let $(a,b)$ be the 'top right hand' vertex of the triangle.
Let $\gcd(a,b)=d$ and $a=pd,b=qd$ .
All dots $(x,y)$ lying on the hypotenuse have a property $\dfrac yx=\dfrac ba$ because they have same slope.
And $\dfrac ba = \dfrac qp$ in lowest term.
So all $(x,y)$ can be written as $pk,qk$ for $k=0,1,\cdots,d$
Number of required dots $=d+1=\gcd(a,b)+1$

展豪張 - 5 years, 2 months ago

as given in the question length of the legs is given (36750,35672) , so that must be the the co ordinates of the top of right angle triangle.also if they are then 8\6 is not equal to 36750\35672..... getting too much confused.. please help..

Deepansh Jindal - 5 years, 2 months ago

@Deepansh Jindal – The (8,6) is just an example to illustrate the idea of the question. The actual question is asking about (36750,35672)

展豪張 - 5 years, 2 months ago

How Many Dots?

1 solution

0 pending reports