How Many Squares Does the Diagonal Cross ? Edited
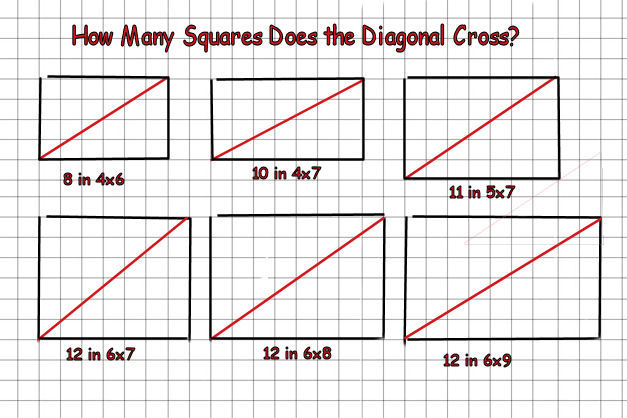 A diagonal is drawn on the floor from 1 corner to the opposite corner of a rectangular room covered with square tiles 1' x 1'.
A diagonal is drawn on the floor from 1 corner to the opposite corner of a rectangular room covered with square tiles 1' x 1'.
A number of tiles are crossed by the diagonal. This depends on the size of the room and the relation of the width and the length.
Let A = # of tiles crossed in a room 32' x 48',
B = # of tiles crossed in a room 32' x 47',
and C = # of tiles crossed in a room 32' x 46'
Find the sum A + B + C
The answer is 218.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Would you please explain how you got the formula?
Log in to reply
I had to solve a question like this and the formula was the solution.
Log in to reply
I'd be very happy to see the solution.
Log in to reply
@Agnishom Chattopadhyay – Sharky has posted the solution. Look above.
Log in to reply
@Guiseppi Butel – That is not what I mean
Log in to reply
@Agnishom Chattopadhyay – Formulas are developed by viewing the results for many different parameters and then devising a formula to accommodate all the results.
Haven't seen this formula before but developed the same method of attack. What started me on this was a problem that had sides 363 and 410. I started thinking about it, wondered about the strange pair of numbers, but later lost the problem and made my own.
Would the answer to the 363, 410 combo be 772?
In a p × q rectangle where g cd ( p , q ) = 1, your journey through tiles can be represented as a string of Us and Rs (U means you cross up, R means you cross right). There will be p − 1 Rs and q − 1 Us, to move over p and up q so starting with the first tile you pass through 1 + ( p − 1 ) + ( q − 1 ) = p + q − 1 tiles.
g cd ( m , n ) m and g cd ( m , n ) n are relatively prime, so imagine g c d ( m , n ) blocks of this size across the diagonal of the room. Each block meets the next at a multiple of ( g cd ( m , n ) m , g cd ( m , n ) n ) , a corner of a tile where you move up and right without entering any tile not counted in a path through a block. So there are g cd ( m , n ) ( g cd ( m , n ) m + g cd ( m , n ) n − 1 ) = m + n − g cd ( m , n ) tiles crossed by a m × n path.
Interesting as a computational geometry problem. Mind you, this solution is only brute force and could be radically improved upon.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
|
Here are some convention I used to solve the problem
I used ! for multiplication, as I was unable to use the star symbol *
[x] - greatest integer >=x
{x} - least integer <=x
Approach: For a square of mXn. I am trying to check how many squares the diagnal crossed for every unit of n.
Lets take the figure 4X6 described in the question m=4, n=6
Assume x axis along the line of 'n'. and Y axis over line m. and bottom left corner to be origin.
For every unit increment in x, y increases by m/n(=4/6)
For x -> 0 to 1 y -> 0 to 4/6
No of squares crossed by diagnal in band x -> 0 to 1 = 1 = {4/6} - [0]
For x -> 1 to 2 y -> 4/6 to 2!4/6
No of squares crossed by diagnal in band x -> 1 to 2 = 2 = {2!4/6} - [4/3]
For x -> 2 to 3 y -> 2!4/6 to 3!4/6
No of squares crossed by diagnal in band x -> 2 to 3 = 1 = {3!4/6} - [2!4/3] ...
Generalizing for mXn square
b=m/n
no of squares crossed in band n from a to a+1 , a is integer and a<n-1 == {(a+1)b}-[ab]
So total no of squares crossed = ({b}+{2b}+....+{nb}) - ([b]+[2b]+....+[(n-1)b])
Now for 32X48 m=32, n=48,b=32/48
No of squares crossed = ({32/48}+{2!32/48}+...+{48!32/48}) - ([32/48]+[2!32/48]+....+[47!32/48]) = (1+2+2+3+4+4+.....+31+32+32) (0+1+2+2+3+4+4+.....+30+30+31) =64
You can find the pattern above, all the even numbers are repeated twice wheareas all the odd numbers occur only once
Similarly you can find such pattern for 32X46 and 32X47 and solve them to be 76 and 78 respectively
So the answer is 64+76+78 = 218
Please let me know if my presentation is not good enough to convey my thoughts....
I have done a question like this before.
For any sized room with side lengths m and n , the number of tiles(T) that are crossed from the diagonal can be shown by the formula:
m + n − H C F ( m , n ) = T
Substituting the values and simplifying, we get
A = 3 2 + 4 8 − H C F ( 3 2 , 4 8 )
A = 6 4
B = 3 2 + 4 7 − H C F ( 3 2 , 4 7 )
B = 7 8
C = 3 2 + 4 6 − H C F ( 3 2 , 4 6 )
C = 7 6
Adding these up, we get
6 4 + 7 8 + 7 6 = 2 1 8
218 is the answer.