How Many Truth-tellers?
Alex, Bella, Chris and David are each either a truth-teller who always tells the truth, or a liar who always lies.
They were each asked, "Out of the 4 of you, how many are truth-tellers?"
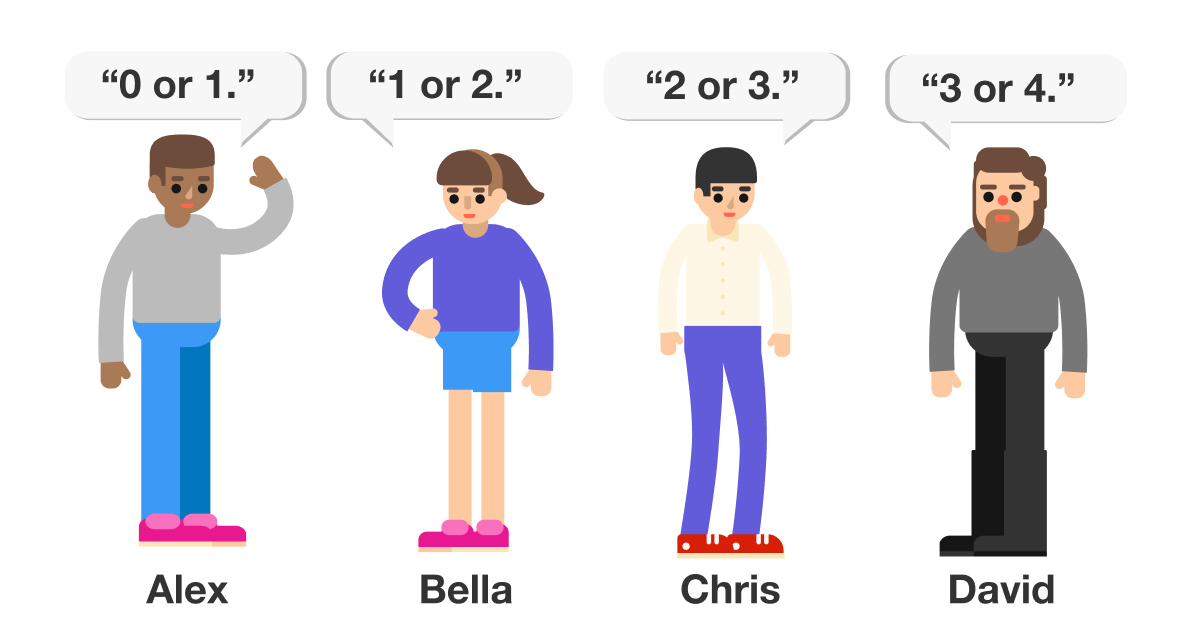
How many of them are truth-tellers?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Well, in real life, yes but if it is an "or" statement, it is true if either part-statement is true. And liars don't give true statements.
Sorry for our screw up when we were editing your problem. Thanks for reposting it.
No problem, maybe I could have waited for a little more, so I wouldn't have had to remove and repost this problem.
Log in to reply
FYI In future, you can select "report problem" (from the menu) to notify us of any issues, and we can fix them accordingly.
wouldn't a truth teller give an exact answer? not "or"?
Log in to reply
Well, a truth-teller simply tells the truth. It doesn't mean that he must tell the truth in the most concise / accurate manner. For example, to a yes/no question, replying with "The answer is yes or no" is a true statement, though it doesn't tell you what the answer actually is.
Of course, if you tried such a tactic in a court of law, you may be thrown into jail for contempt of court.
Log in to reply
The question is precise, "how many" - you can't use 0 or 1 as a truth teller as you know that 0 cannot be correct
Log in to reply
@Graham Mercer – There is no need to be perfectly precise when giving an answer as a truthteller. If there are 2 truthtellers, then "there are at least one and at most 2 truthtellers" is a true statement, as is the equivalent statement of "there is 1 or 2 truthtellers". Because it is phrased with an "or", all that is means is "one of these statements is true".
I agree that the truthteller cannot say "There is 1 truthteller".
I thought about the problem more generally:
Suppose N ≥ 3 people respond to the question, "How many among you are truth-tellers?", and akin to the scenario in Tarmo's original problem, suppose:
- the first person says, "0 or 1."
- the second says, "1 or 2."
- and so on, until the last person says, "N-1 or N."
Now, the number of truth-tellers is at least 0 and at most N. Let's embark on a case analysis:
Case 1: If the number of truth-tellers is 0 or N, then 1 statement is true —namely the first or last— and the rest are false.
Case 2: If the number of truth-tellers is strictly between 0 and N, then 2 consecutive statements are true and the rest are false. (For example, if there are 100 people and 5 are truth-tellers, the only true statements are "4 or 5" and "5 or 6".)
Thus by case analysis, we conclude that the number of truth-tellers is 1 or 2 — which is precisely the second person's answer. † Therefore the second person is a truth-teller.
The above case analysis also tells us that if a statement other than the first or last is true, then we must be in the second case in which 2 statements are true. This is indeed the case we are in, for the second statement is true. ‡ Hence exactly 2 statements are true, namely "1 or 2" and "2 or 3".
† If N = 1, there is no second person, so the argument fails at this point. In this case, there is only one person, and that person says, "0 or 1.", which is true.
‡ If N = 2, the second person is the last person, so the argument fails at this point. Indeed, in this case, the problem statement is inconsistent.
Nice! This solution clearly explains that the answer would be the same even if there were eg. one hundred people instead with their statements.
Consider the generalization described by Jeremy Weissmann, with N persons.
Since there are N persons, the count of truth tellers is a number in the range 0 through N . Given all the answers, there must be one or two persons who told the truth, since each count is mentioned either once (viz. 0 and N ) or twice.
If the count would be one, then there would be two truth-tellers (the two persons who said the disjunct “1”). Contradiction! So, the count equals 2, and the truth tellers are the ones answering “1 or 2” and “2 or 3”.
The only quantity that matches with its own frequency (of how many times it was mentioned in the interview conversation) is 2, so Bella and Chris are 2 truth tellers while Alex and David are 2 liars.
- OR statement would be true if there exist at least one truth within it.
Relevant wiki: Truth-Tellers and Liars
If there are 0 truth-tellers, Alex would be a truth-teller, stating "0 or 1." However, that would mean there is 1 truth-teller which contradicts the original assumption "There are 0 truth-tellers."
If there is 1 truth-teller, Alex and Bella would be truth-tellers, stating "0 or 1" and "1 or 2". However, that would mean there are 2 truth-tellers which contradicts the original assumption "There is 1 truth-teller."
If there are 2 truth-tellers, Bella and Chris would be truth-tellers, stating "1 or 2" and "2 or 3". This means Bella and Chris are the 2 truth-tellers and the original assumption is satisfied.
If there are 3 truth-tellers, Chris and David would be truth-tellers, stating "2 or 3" and "3 or 4". However, that would mean there are 2 truth-tellers which contradicts the original assumption "There are 3 truth-tellers."
If there are 4 truth-tellers, David would be a truth-teller, stating "3 or 4.". However, that would mean there is 1 truth-teller which contradicts the original assumption "There are 4 truth-tellers."
Therefore, the only possible number of truth-tellers is 2 .