How much of the octagon is left?
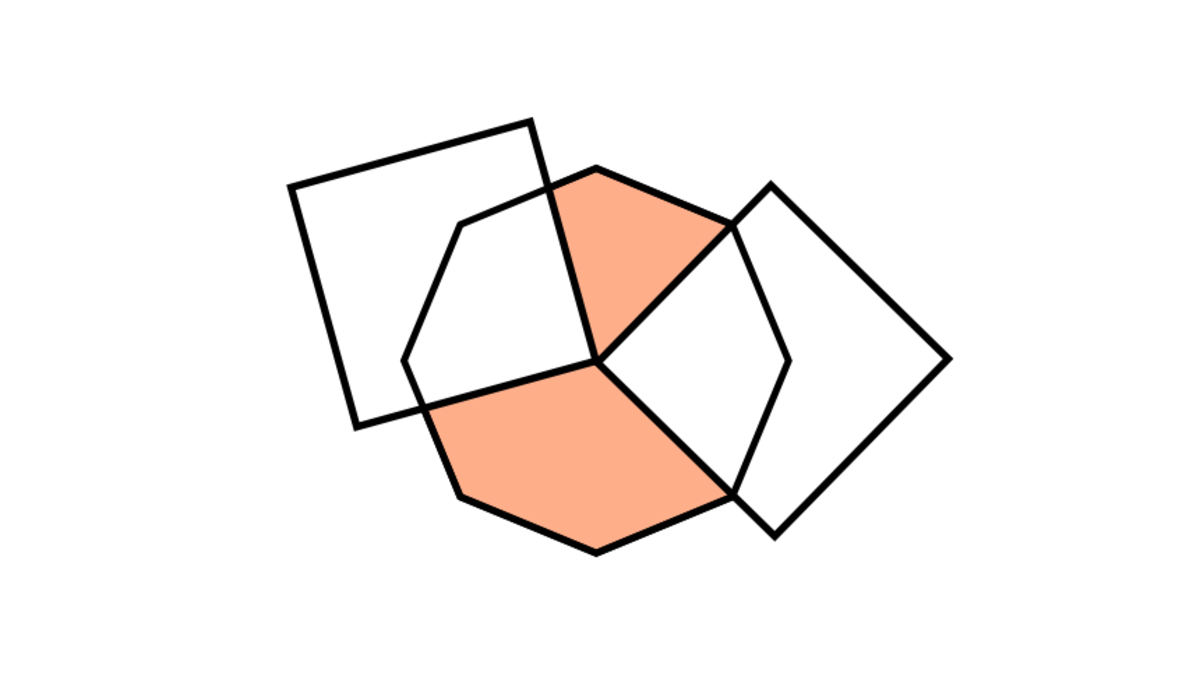
Two squares are drawn with one vertex at the center of the octagon. The overlapped area is removed. How much of the octagon is left (ratio of peach area to the area of octagon)?
Inspiration: How much is covered
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
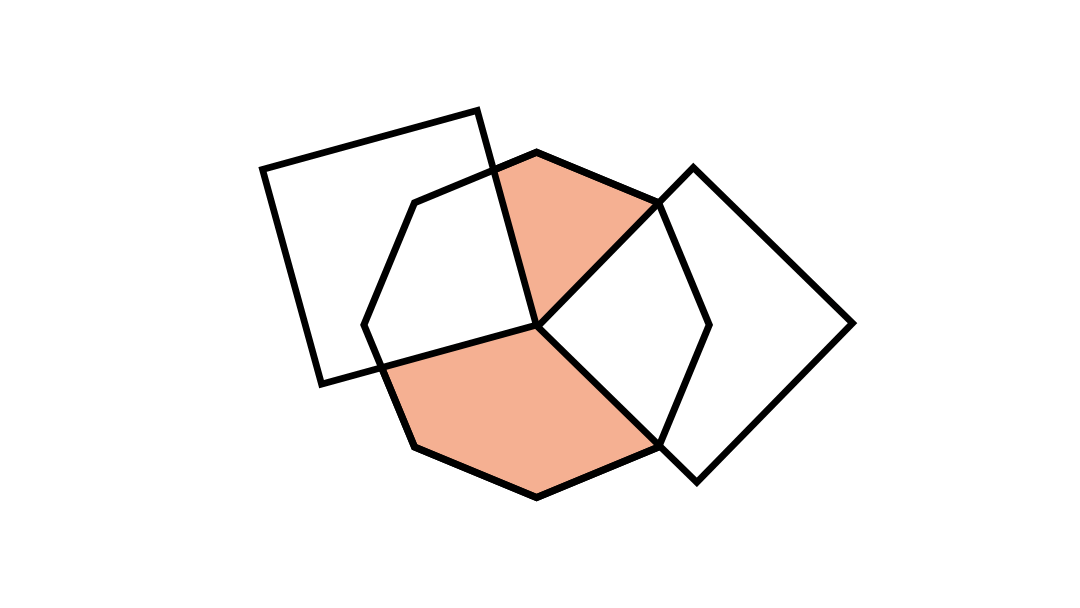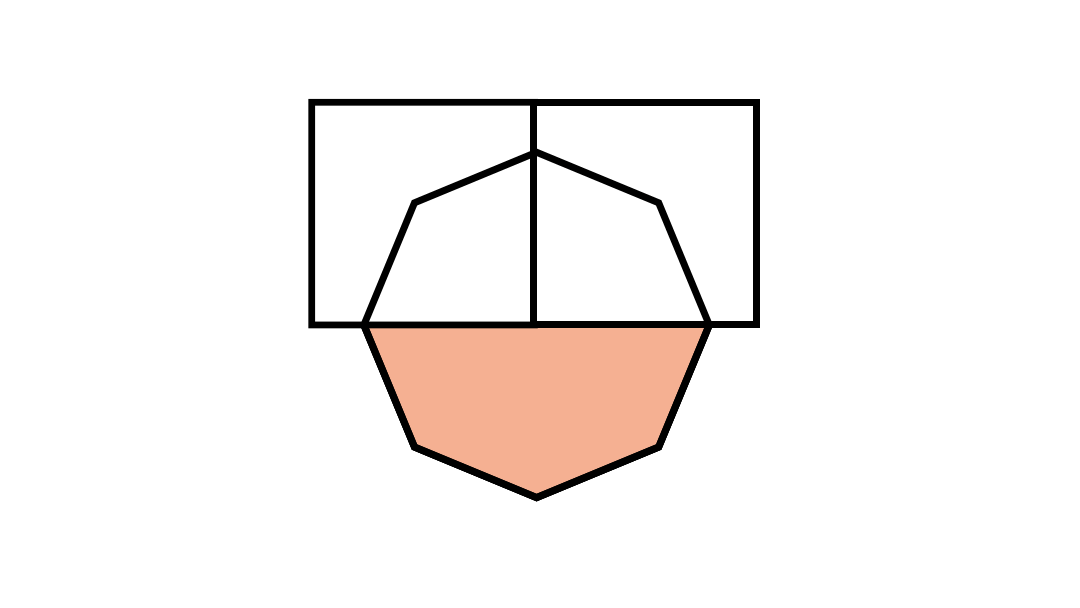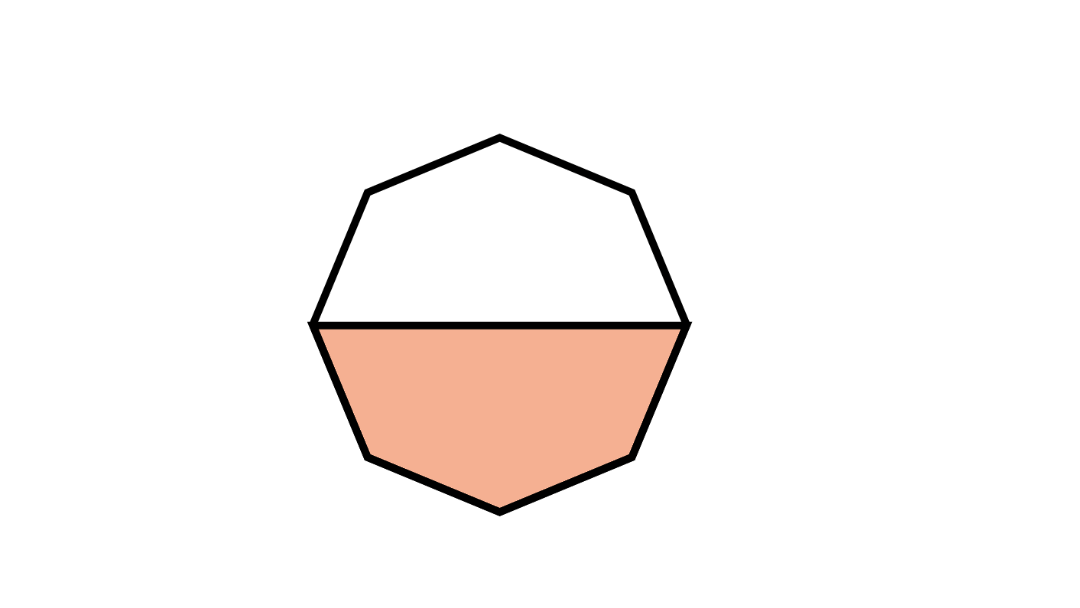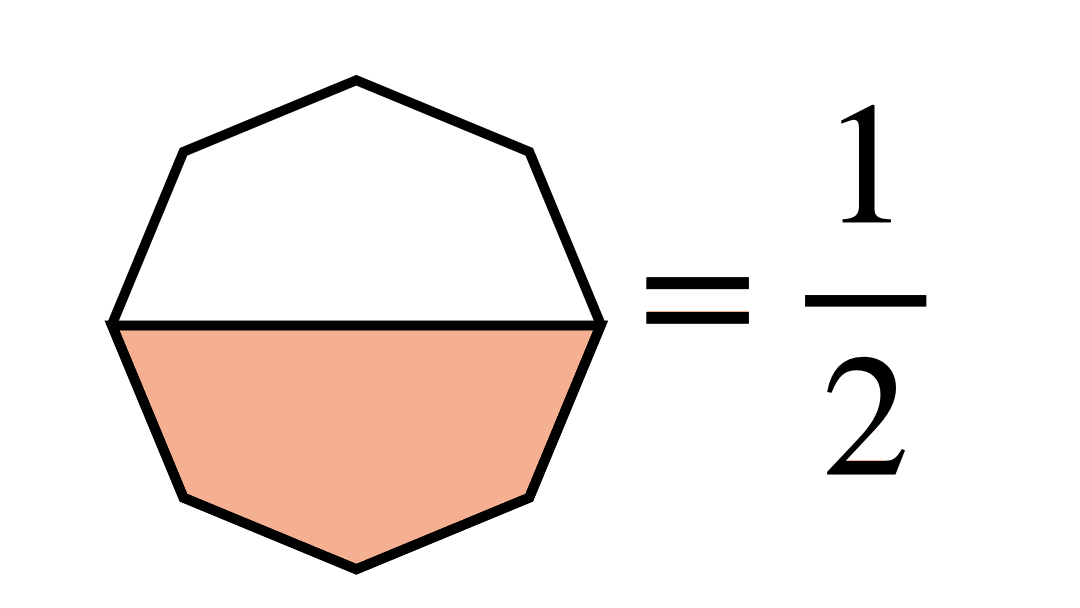
The explanation : Interior angle of a square is 9 0 ∘ . Two squares combined form 1 8 0 ∘ . The ratio will be this combined angle divided over the entire angle of point which is 3 6 0 ∘
3 6 0 ∘ 1 8 0 ∘ = 2 1
Log in to reply
And what about squares in hexagon?
Log in to reply
For any n-sided polygon, the answer will remain half always. Since there are 3 6 0 ∘ around a point and the total made by squares is 1 8 0 ∘ . Thus it will always be 2 1
Log in to reply
@Mahdi Raza – I don't believe it is true. For example it will not work with triangle.
@Mahdi Raza – Umm, yeah but maybe when the line is going through the centre and one of the vertex. Though not always! Thanks for pointing it out
Divide the octagon into 8 congruent triangles and swap the triangles labeled A and B below:
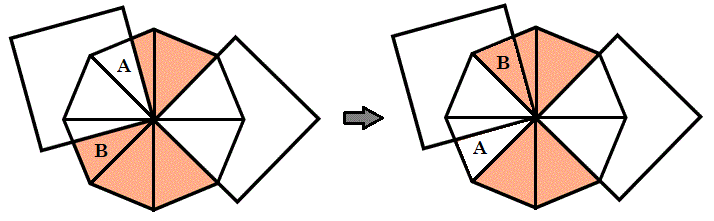
Then 4 out of 8 congruent triangles are colored peach, so the ratio of the peach area to the area of the octagon is 8 4 = 2 1 .
@David Vreken +1!